Mệnh đề đúng?
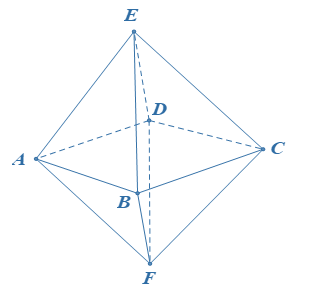
Một hình đa diện có các mặt là những tam giác. Gọi M là tổng số mặt và C là tổng số cạnh của đa diện đó. Mệnh đề nào sau đây đúng.
Vì mỗi mặt là những tam giác nên có tổng số cạnh là 3M. Mỗi cạnh là cạnh chung của đúng hai mặt nên ta có hệ thức 3M = 2C.