Tính độ dài đoạn thẳng MN
Trong không gian với hệ trục tọa độ ![]() cho đường thẳng
cho đường thẳng ![]() và mặt cầu
và mặt cầu ![]() . Hai mặt phẳng (P) và (Q) chứa d và tiếp xúc với (S). Gọi M và N là tiếp điểm. Độ dài đoạn thẳng MN bằng
. Hai mặt phẳng (P) và (Q) chứa d và tiếp xúc với (S). Gọi M và N là tiếp điểm. Độ dài đoạn thẳng MN bằng
Hình vẽ minh họa
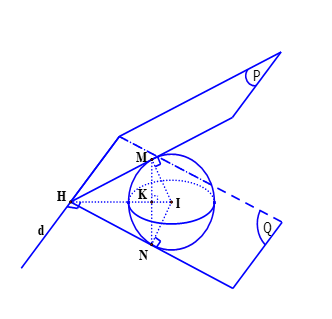
Từ Tâm
và bán kính
Từ Vectơ
Hạ
Xét tam giác vuông tại M ta có:
.
Ta có
.
.







