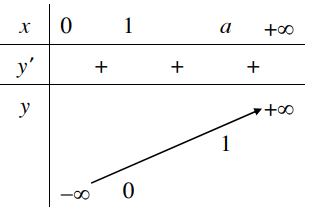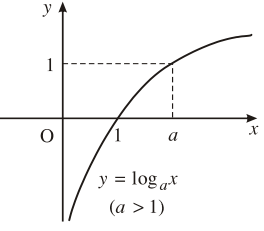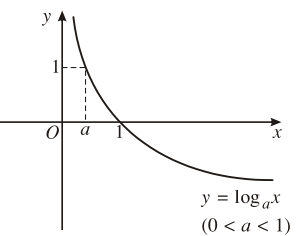Hàm số lôgarit
Bài học Lí thuyết toán 12: Hàm số lôgarit giới thiệu cho các em khái niệm về hàm số lôgarit, công thức tính đạo hàm và khảo sát hàm số lôgarit. Bên cạnh đó là các ví dụ bài tập có lời giải chi tiết giúp các em dễ dàng ôn tập củng cố.
1. Định nghĩa
Cho 
\(a\) là số thực dương và \(a \ne 1\).
Hàm số \(y = \log_{a}x\) được gọi là hàm số lôgarit cơ số \(a\).
Ví dụ:
Hàm số \(y = \log_{2}x\) được gọi là hàm số lôgarit cơ số 2.
2. Đạo hàm
- Hàm số \(y = \log_{a}x\) \((a>0, a \ne 1)\) có đạo hàm tại mọi \(x>0\)
\((\log_{a}x)' = \frac{1}{x \ln a}\)
\((\ln x)'=\frac{1}{x}\)
- Ngoài ra, đối với hàm hợp \(y = \log_{a}u(x)\), ta có công thức tính đạo hàm:
\((\log_{a}u)'=\frac {u'}{u\ln a }\)
Ví dụ: Tính đạo hàm của hàm số \(y = ({x^2} + 2x){e^{ - x}}\)?
Giải:
Ta có: \(y = \left( {{x^2} + 2x} \right){e^{ - x}} \Rightarrow {y^/} = {\left( {{x^2} + 2x} \right)^/}{e^{ - x}} + {\left( {{e^{ - x}}} \right)^/}\left( {{x^2} + 2x} \right)\)
\(\Rightarrow {y^/} = \left( {2x + 2} \right){e^{ - x}} - {e^{ - x}}\left( {{x^2} + 2x} \right) = \left( { - {x^2} + 2} \right){e^{ - x}}\)
3. Khảo sát hàm số \(y = \log_{a}x\) \((a>0, a \ne 1)\)
| \(y = \log_{a}x\), \(a>1\) |
\(y = \log_{a}x\), \(0 < a < 1\) |
1.Tập xác định
|
1.Tập xác định
|
2. Sự biến thiên
Giới hạn đặc biệt:
Tiệm cận: Trục Oy là tiệm cận đứng |
2. Sự biến thiên
Giới hạn đặc biệt:
Tiệm cận: Trục Oy là tiệm cận đứng |
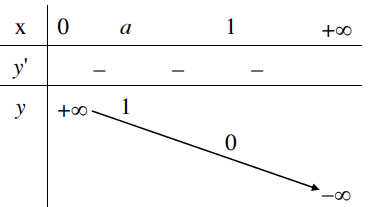
3. Bảng biến thiên
|
3. Bảng biến thiên
|
4. Đồ thị
Đi qua các điểm |
4. Đồ thị
Đi qua các điểm |
Ví dụ:
Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số nào?
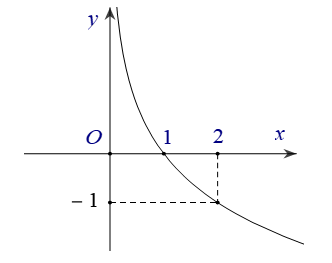
Giải:
Ta xét đồ thị hàm số đã cho là đồ thị của \(y = \log_{a}x\).
Vì điểm \(A(2;-1)\) thuộc đồ thị hàm số nên \(- 1 = {\log _a}2 \Rightarrow {a^{ - 1}} = 2 \Rightarrow \frac{1}{a} = 2 \Rightarrow a = 0,5\).
Suy ra đồ thị trên là đồ thị của hàm số \(y = {\log _{0,5}}x\).
