Khoảng cách và góc
Bài học Lí thuyết toán 12: Khoảng cách và góc là phần kiến thức tiếp theo của phương trình mặt phẳng, bao gồm điều kiện để xét vị trí tương đối của 2 mặt phẳng, công thức tính khoảng cách từ một điểm đến một mặt phẳng và góc giữa hai mặt phẳng. Trong từng mục khi đưa ra công thức luôn kèm theo các ví dụ bài tập có hướng dẫn giải chi tiết, xây dựng dựa trên kiến thức trọng tâm chương trình Toán 12 và các câu hỏi trong đề thi THPT Quốc gia. Hi vọng các em sẽ ôn tập hiệu quả, hướng đến đạt mục tiêu trong các kì thi lớn sắp tới.
1. Điều kiện để xét vị trí tương đối
Trong không gian 
\(Oxyz\), cho hai mặt phẳng:
\(\left( \alpha \right):{A_1}x + {B_1}y + {C_1}z + {D_1} = 0\)
\(\left( \beta \right):{A_2}x + {B_2}y + {C_2}z + {D_2} = 0\)
Khi đó, \((\alpha )\) và \(\left( \beta \right)\) có hai vecto pháp tuyến tương ứng là:
\(\vec n_1 = (A_1;B_1;C_1)\)
\(\vec n_2 = (A_2;B_2;C_2)\)
Xét vị trí tương đối của \((\alpha_1 )\) và \(\left( \alpha_2 \right)\) có 4 trường hợp như sau:
TH1: \((\alpha_1 ) \equiv (\alpha_2)\)
TH2: \((\alpha_1 ) \parallel (\alpha_2)\)
TH3: \((\alpha_1 ) \cap (\alpha_2)\)
TH4: \((\alpha_1 ) \perp (\alpha_2)\)
1.1. Điều kiện để hai mặt phẳng trùng nhau
Để hai mặt phẳng \((\alpha_1 )\) và \(\left( \alpha_2 \right)\) trùng nhau thì \(\vec n_1\) phải cùng phương với \(\vec n_2\).
Mặt khác \(D_1=kD_2\). Ta có hệ sau:
\((\alpha_1) \equiv (\alpha_2) \Leftrightarrow \left\{ \begin{gathered} {{\vec n_1}=k \vec n_2}\,\\ D_1= kD_2 \\ \end{gathered} \right.\) \(\Leftrightarrow \left\{ \begin{gathered}
{(A_1; B_1; C_1)=k(A_2;B_2;C_2)}\,\\
D_1= kD_2 \\
\end{gathered} \right.\)
Vậy \((\alpha_1) \equiv (\alpha_2) \Leftrightarrow\) \(\frac{{{A_1}}}{{{A_2}}} = \frac{{{B_1}}}{{{B_2}}} = \frac{{{C_1}}}{{{C_2}}} \ne \frac{{{D_1}}}{{{D_2}}}\).
1.2. Điều kiện để hai mặt phẳng song song
Để hai mặt phẳng \((\alpha_1 )\) và \(\left( \alpha_2 \right)\) song song thì \(\vec n_1\) phải cùng phương với \(\vec n_2\). Mặt khác \(D_1 \neq kD_2\). Ta có hệ sau:
\((\alpha_1) \parallel (\alpha_2) \Leftrightarrow \left\{ \begin{gathered} {{\vec n_1}=k \vec n_2}\,\\ D_1 \neq kD_2 \\ \end{gathered} \right.\) \(\Leftrightarrow \left\{ \begin{gathered} {(A_1; B_1; C_1)=k(A_2;B_2;C_2)}\,\\ D_1 \neq kD_2 \\ \end{gathered} \right.\)
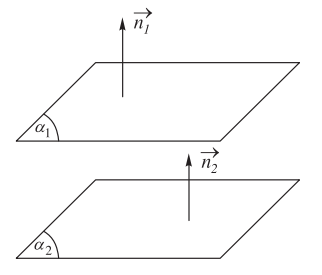
Vậy \((\alpha_1) \parallel (\alpha_2) \Leftrightarrow\)\(\frac{{{A_1}}}{{{A_2}}} = \frac{{{B_1}}}{{{B_2}}} = \frac{{{C_1}}}{{{C_2}}} = \frac{{{D_1}}}{{{D_2}}}\)
Ví dụ:
Trong không gian \(Oxyz\), viết phương trình mặt phẳng \((P)\) đi qua điểm \(M(0;1;3)\) và song song với mặt phẳng \((Q):2x - 3z + 1 = 0\).
Giải:
- Mặt phẳng \((P)\) song song với mặt phẳng \((Q):2x - 3z + 1 = 0\) nên mặt phẳng \((P)\) có phương trình dạng: \(2x - 3z + D = 0\,\,\,(D \ne 1)\).
- Mặt khác, mặt phẳng \((P)\) đi qua điểm \(M(0;1;3)\) nên thay tọa độ điểm \(M\) vào phương trình mặt phẳng phải thỏa mãn. Ta được: \(2.0 - 3.3 + D = 0 \Leftrightarrow D = 9\) (thỏa mãn \(D \ne 1\)).
\(\Rightarrow\) Vậy phương trình mặt phẳng \((P)\) là: \(2x - 3z + 9 = 0\).
1.3. Điều kiện để hai mặt phẳng cắt nhau
Để hai mặt phẳng \((\alpha_1 )\) và \(\left( \alpha_2 \right)\) cắt nhau thì \(\vec n_1\) không cùng phương với \(\vec n_2\). Ta có:
\((\alpha_1) \cap (\alpha_2) \Leftrightarrow \vec n_1 \neq k \vec n_2\) \(\Leftrightarrow {(A_1; B_1; C_1) \neq k(A_2;B_2;C_2)}\)
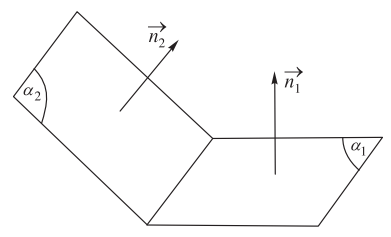
Vậy \((\alpha_1) \cap (\alpha_2) \Leftrightarrow\) \(\frac{{{A_1}}}{{{A_2}}} \ne \frac{{{B_1}}}{{{B_2}}} \vee \frac{{{B_1}}}{{{B_2}}} \ne \frac{{{C_1}}}{{{C_2}}} \vee \frac{{{A_1}}}{{{A_2}}} \ne \frac{{{C_1}}}{{{C_2}}}\)
1.4. Điều kiện để hai mặt phẳng vuông góc
Để hai mặt phẳng \((\alpha_1 )\) và \(\left( \alpha_2 \right)\) vuông góc thì \(\vec n_1\) cũng phải vuông góc với \(\vec n_2\). Ta có:
\((\alpha_1) \perp (\alpha_2) \Leftrightarrow \vec n_1 . \vec n_2 =0\) \(\Leftrightarrow A_1.A_2+ B_1.B_2+ C_1.C_2=0\)
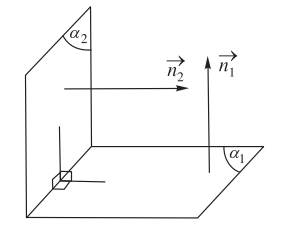
Vậy \((\alpha_1) \perp (\alpha_2)\)\(\Leftrightarrow A_1.A_2+ B_1.B_2+ C_1.C_2=0\)
Ví dụ:
Trong không gian \(Oxyz\), viết phương trình mặt phẳng \((\alpha )\) đi qua điểm \(A(1;2; - 2)\,,B(2; - 1;4)\) và vuông góc với \(\left( \beta \right):x - 2y - z + 1 = 0\)
Giải:
Có \(\overrightarrow {AB} = \left( {1; - 3;6} \right)\)
Mặt phẳng \(\left( \beta \right)\) có VTPT là \(\overrightarrow {{n_\beta }} = \left( {1; - 2; - 1} \right)\).
Mặt phẳng \((\alpha )\) chứa A, và vuông góc với \(\left( \beta \right)\) nên có một vectơ pháp tuyến là: \(\overrightarrow {{n_\alpha }} = \left[ {\overrightarrow {AB} ,\overrightarrow {{n_\beta }} } \right] = \left( {15;7;1} \right)\).
Phương trình mặt phẳng \((\alpha )\) là: \(15x + 7z + 1 - 27 = 0\).
2. Khoảng cách từ một điểm đến một mặt phẳng
Trong không gian \(Oxyz\), cho điểm \({M_0}({x_0};{y_0};{z_0})\) và mặt phẳng \(\left( \alpha \right):Ax + By + Cz + D = 0\)
Khi đó khoảng cách từ điểm \(M_0\) đến mặt phẳng \((\alpha )\) được tính:
\(d({M_0},(\alpha )) = \frac{{|A{x_0} + B{y_0} + C{z_0} + D|}}{{\sqrt {{A^2} + {B^2} + {C^2}} }}\)
Ví dụ 1: Trong không gian \(Oxyz\), tính khoảng cách giữa 2 mặt phẳng song song sau:
\((P): x+2y+2z+2024=0\)
\((Q): x+2y+2z+2=0\)
Giải:
Vì khoảng cách giữa hai mặt phẳng song song bằng khoảng cách từ 1 điểm bất kì thuộc mặt phẳng này đến mặt phẳng kia
Ta lấy điểm \(M(0;0;-1) \in (Q)\)
Áp dụng công thức, có: \(d((P),(Q))=d(M,(P))=\dfrac{|0+2.0+2.(-1)+2024|}{\sqrt{1^2+c^2+2^2}}=\dfrac{2022}{3} =674\)
Vậy \(d((P),(Q))=674\).
Ví dụ 2: Trong không gian \(Oxyz\), viết phương trình mặt phẳng \((P)\) song song với mặt phẳng \((Q):x + 2y - 2z + 1 = 0\) và \((P)\) cách điểm \(M(1; - 2;1)\) một khoảng bằng 3.
Lời giải
Do \((P)\) song song với mặt phẳng \((Q):x + 2y - 2z + 1 = 0\) nên phương trình của mặt phẳng \((P)\) có dạng: \(x + 2y - 2z + D = 0\) với \(D \ne 1\).
Vì \(d(M,(P)) = 3\) \(\Leftrightarrow \frac{{|1 - 4 - 2 + D|}}{{\sqrt {{1^2} + {2^2} + {{( - 2)}^2}} }} = 3\) \(\Leftrightarrow | - 5 + D| = 9\)
\(\Leftrightarrow \left[ \begin{gathered}
D = - 4 \hfill \\
D = 14 \hfill \\
\end{gathered} \right.\)
Vậy có hai mặt phẳng thỏa mãn yêu cầu bài toán: \(x + 2y - 2z - 4 = 0\) và \(x + 2y - 2z + 14 = 0\).
3. Góc giữa hai mặt phẳng
Trong không gian , cho hai mặt phẳng \(\left( \alpha \right):{A_1}x + {B_1}y + {C_1}z + {D_1} = 0\) và \(\left( \beta \right):{A_2}x + {B_2}y + {C_2}z + {D_2} = 0\)
Góc giữa \((\alpha )\) và \(\left( \beta \right)\) bằng hoặc bù với góc giữa hai VTPT \(\overrightarrow {{n_\alpha }} ,\overrightarrow {{n_\beta }}\) . Tức là:
\(\cos \left( {\left( \alpha \right),\left( \beta \right)} \right) = \left| {\cos \left( {\overrightarrow {{n_\alpha }} ,\overrightarrow {{n_\beta }} } \right)} \right|\)\(= \frac{{\left| {\overrightarrow {{n_\alpha }} .\overrightarrow {{n_\beta }} } \right|}}{{\left| {\overrightarrow {{n_\alpha }} } \right|.\left| {\overrightarrow {{n_\beta }} } \right|}} = \frac{{\left| {{A_1}{A_2} + {B_1}{B_2} + {C_1}{C_2}} \right|}}{{\sqrt {A_1^2 + B_1^2 + C_1^2} .\sqrt {A_2^2 + B_2^2 + C_2^2} }}\)
Ví dụ:
Trong không gian với hệ trục tọa độ \(Oxyz\), gọi \((P)\) là mặt phẳng chứa trục \(Oy\) và tạo với mặt phẳng \(y + z + 1 = 0\) góc \(60^0\). Viết phương trình mặt phẳng \((P)\) ?
Giải:
+) Mặt phẳng \((P)\) chứa trục \(Oy\) nên có dạng: \(Ax + Cz = 0\;\;({A^2} + {C^2} \ne 0)\).
+) Mặt phẳng \((P)\) tạo với mặt phẳng \(y + z + 1 = 0\) góc \(60^0\) nên \(\cos {60^0} = \frac{{\left| {\overrightarrow {{n_{(P)}}} .\overrightarrow {{n_{(Q)}}} } \right|}}{{\left| {\overrightarrow {{n_{(P)}}} } \right|.\left| {\overrightarrow {{n_{(Q)}}} } \right|}}\).
\(\Leftrightarrow \frac{1}{2} = \frac{{\left| C \right|}}{{\sqrt {{A^2} + {C^2}} .\sqrt 2 }} \Leftrightarrow \sqrt {{A^2} + {C^2}} = \sqrt 2 \left| C \right|\)
\(\Leftrightarrow {A^2} - {C^2} = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}
{A = C} \\
{A = - C}
\end{array}} \right.\)
Phương trình mặt phẳng \((P)\) là: \(\left[ \begin{gathered}
x - z = 0 \hfill \\
x + z = 0 \hfill \\
\end{gathered} \right.\)
