Giải SBT Toán 12 bài 1: Hệ tọa độ trong không gian

Giải SBT Toán lớp 12

Hình học 12 - Hệ tọa độ trong không gian

VnDoc xin giới thiệu tới thầy cô và các bạn học sinh tài liệu Giải SBT Toán 12 bài 1: Hệ tọa độ trong không gian, với nội dung tài liệu được tổng hợp chính xác sẽ là nguồn thông tin hay để phục vụ công việc học tập của các bạn học sinh được tốt hơn.

Giải SBT Toán 12: Đề kiểm tra - Chương 1. Khối đa diện

Giải SBT Toán 12 bài 2: Mặt cầu

Giải SBT Toán 12: Đề toán tổng hợp - Chương 2. Mặt nón, mặt trụ, mặt cầu

Giải SBT Toán 12: Đề kiểm tra - Chương 2. Mặt nón, mặt trụ, mặt cầu

Giải SBT Toán 12 bài 1

Bài 3.1 trang 102 sách bài tập (SBT) – Hình học 12

Trong không gian Oxyz cho ba vecto $\underset{a}{\rightarrow}$ $\underset{a}{\rightarrow}$=(2;−1;2), $\underset{b}{\rightarrow}$ $\underset{b}{\rightarrow}$=(3;0;1), $\underset{c}{\rightarrow}$ $\underset{c}{\rightarrow}$=(−4;1;−1). Tìm tọa độ của các vecto $\underset{m}{\rightarrow}$ $\underset{m}{\rightarrow}$ và $\underset{n}{\rightarrow}$ $\underset{n}{\rightarrow}$ biết rằng:

a) $\underset{m}{\rightarrow}$ $\underset{m}{\rightarrow}$=3 $\underset{a}{\rightarrow}$ $\underset{a}{\rightarrow}$−2 $\underset{b}{\rightarrow}$ $\underset{b}{\rightarrow}$+ $\underset{c}{\rightarrow}$ $\underset{c}{\rightarrow}$

b) $\underset{m}{\rightarrow}$ $\underset{m}{\rightarrow}$=2 $\underset{a}{\rightarrow}$ $\underset{a}{\rightarrow}$+ $\underset{b}{\rightarrow}$ $\underset{b}{\rightarrow}$+4 $\underset{c}{\rightarrow}$ $\underset{c}{\rightarrow}$

Hướng dẫn làm bài

$\underset{m}{\rightarrow}$ $\underset{m}{\rightarrow}$=(−4;−2;3), $\underset{n}{\rightarrow}$ $\underset{n}{\rightarrow}$=(−9;2;1)

Bài 3.2 trang 102 sách bài tập (SBT) – Hình học 12

Trong không gian Oxyz cho vecto $\underset{a}{\rightarrow}$ $\underset{a}{\rightarrow}$=(1;−3;4)

a) Tìm y₀ và z₀ để cho vecto $\underset{b}{\rightarrow}$ $\underset{b}{\rightarrow}$=(2;y₀;z₀) cùng phương với $\underset{a}{\rightarrow}$ $\underset{a}{\rightarrow}$

b) Tìm tọa độ của vecto $\underset{c}{\rightarrow}$ $\underset{c}{\rightarrow}$ biết rằng $\underset{a}{\rightarrow}$ $\underset{a}{\rightarrow}$ và $\underset{c}{\rightarrow}$ $\underset{c}{\rightarrow}$ ngược hướng và | $\underset{c}{\rightarrow}$ $\underset{c}{\rightarrow}$|=2| $\underset{a}{\rightarrow}$ $\underset{a}{\rightarrow}$|

Hướng dẫn làm bài:

a) Ta biết rằng $\underset{a}{\rightarrow}$ $\underset{a}{\rightarrow}$ và $\underset{b}{\rightarrow}$ $\underset{b}{\rightarrow}$ cùng phương khi và chỉ khi $\underset{a}{\rightarrow}$ $\underset{a}{\rightarrow}$=k $\underset{b}{\rightarrow}$ $\underset{b}{\rightarrow}$ với k là một số thực. Theo giả thiết ta có: $\underset{b}{\rightarrow}$ $\underset{b}{\rightarrow}$=(x₀;y₀;z₀) với x₀ = 2. Ta suy ra k=1/2 nghĩa là l=1/2x₀

Do đó: −3=1/2y₀nên y₀ = -6

4=1/2z₀ nên z₀ = 8

Vậy ta có $\underset{b}{\rightarrow}$ $\underset{b}{\rightarrow}$=(2;−6;8)

b) Theo giả thiết ta có $\underset{c}{\rightarrow}$ $\underset{c}{\rightarrow}$=−2 $\underset{a}{\rightarrow}$ $\underset{a}{\rightarrow}$

Do đó tọa độ của $\underset{c}{\rightarrow}$ $\underset{c}{\rightarrow}$ là: $\underset{c}{\rightarrow}$ $\underset{c}{\rightarrow}$ = (-2; 6; -8)

Bài 3.3 trang 102 sách bài tập (SBT) – Hình học 12

Trong không gian Oxyz cho điểm M có tọa độ (x₀; y₀; z₀). Tìm tọa độ hình chiếu vuông góc của điểm M trên các mặt phẳng tọa độ (Oxy), (Oyz), (Ozx).

Hướng dẫn làm bài:

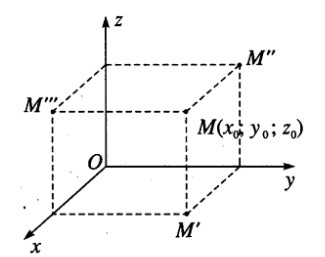
Giải SBT Toán 12 bài 1: Hệ tọa độ trong không gian

Gọi M’, M’’, M’’’ lần lượt là hình chiếu vuông góc của điểm M trên các mặt phẳng (Oxy), (Oyz), (Ozx).

Ta có: M’(x₀; y₀; 0)

M’’ (0; y₀; z₀)

M’’’(x₀; 0; z₀)

Bài 3.4 trang 102 sách bài tập (SBT) – Hình học 12

Cho hai bộ ba điểm:

a) A = (1; 3; 1), B = (0; 1; 2), C = (0; 0; 1)

b) M = (1; 1; 1), N = (-4; 3; 1), P = (-9; 5; 1)

Hỏi bộ nào có ba điểm thẳng hàng?

Hướng dẫn làm bài:

a) Ta có $\underset{AB}{\rightarrow}$ $\underset{AB}{\rightarrow}$=(−1;−2;1)

$\underset{AC}{\rightarrow}$ $\underset{AC}{\rightarrow}$=(−1;−3;0)

Ba điểm A, B, C thẳng hàng khi và chỉ khi hai vecto $\underset{AB}{\rightarrow}$ $\underset{AB}{\rightarrow}$ và $\underset{AC}{\rightarrow}$ $\underset{AC}{\rightarrow}$ cùng phương, nghĩa là $\underset{AB}{\rightarrow}$ $\underset{AB}{\rightarrow}$=k $\underset{AC}{\rightarrow}$ $\underset{AC}{\rightarrow}$ với k là một số thực.

Giả sử ta có $\underset{AB}{\rightarrow}$ $\underset{AB}{\rightarrow}$=k $\underset{AC}{\rightarrow}$ $\underset{AC}{\rightarrow}$, khi đó k.(−1)=−1;k.(−3)=−2;k.(0)=1

Ta không tìm được số k nào thỏa mãn đồng thời cả ba đẳng thức trên. Vậy ba điểm A, B, C không thẳng hàng.

b) Ta có: $\underset{MN}{\rightarrow}$ $\underset{MN}{\rightarrow}$=(−5;2;0) và $\underset{MP}{\rightarrow}$ $\underset{MP}{\rightarrow}$=(−10;4;0). Hai vecto $\underset{MN}{\rightarrow}$ $\underset{MN}{\rightarrow}$ và $\underset{MP}{\rightarrow}$ $\underset{MP}{\rightarrow}$ thỏa mãn điều kiện: $\underset{MN}{\rightarrow}$ $\underset{MN}{\rightarrow}$=k $\underset{MP}{\rightarrow}$ $\underset{MP}{\rightarrow}$ với k=1/2 nên ba điểm M, N, P thẳng hàng.

Bài 3.5 trang 102 sách bài tập (SBT) – Hình học 12

Trong không gian Oxyz, hãy tìm trên mặt phẳng (Oxz) một điểm M cách đều ba điểm A(1; 1; 1), B(-1; 1; 0), C(3; 1; -1).

Hướng dẫn làm bài:

Điểm M thuộc mặt phẳng (Oxz) có tọa độ là (x; 0; z), cần phải tìm x và z. Ta có:

MA² = (1 – x)² + 1 + (1 – z)²

MB² = (–1 – x)² + 1 + z²

MC² = (3 – x)² + 1 + (–1 – z)²

Theo giả thiết M cách đều ba điểm A, B, C nên ta có MA² = MB² = MC²

Từ đó ta tính được M(5/6;0;−7/6)

Bài 3.6 trang 102 sách bài tập (SBT) – Hình học 12

Cho hình tứ diện ABCD. Chứng minh rằng:

a) $\underset{AC}{\rightarrow}$ $\underset{AC}{\rightarrow}$+ $\underset{BD}{\rightarrow}$ $\underset{BD}{\rightarrow}$= $\underset{AD}{\rightarrow}$ $\underset{AD}{\rightarrow}$+ $\underset{BC}{\rightarrow}$ $\underset{BC}{\rightarrow}$

b) $\underset{AB}{\rightarrow}$ $\underset{AB}{\rightarrow}$=1/2 $\underset{AC}{\rightarrow}$ $\underset{AC}{\rightarrow}$+1/2 $\underset{AD}{\rightarrow}$ $\underset{AD}{\rightarrow}$+1/2 $\underset{DC}{\rightarrow}$ $\underset{DC}{\rightarrow}$+ $\underset{BD}{\rightarrow}$ $\underset{BD}{\rightarrow}$

Hướng dẫn làm bài:

a) Ta có:

$\underset{AC}{\rightarrow}$ $\underset{AC}{\rightarrow}$= $\underset{AD}{\rightarrow}$ $\underset{AD}{\rightarrow}$+ $\underset{DC}{\rightarrow}$ $\underset{DC}{\rightarrow}$

$\underset{BD}{\rightarrow}$ $\underset{BD}{\rightarrow}$= $\underset{BC}{\rightarrow}$ $\underset{BC}{\rightarrow}$+ $\underset{CD}{\rightarrow}$ $\underset{CD}{\rightarrow}$

Do đó: $\underset{AC}{\rightarrow}$ $\underset{AC}{\rightarrow}$+ $\underset{BD}{\rightarrow}$ $\underset{BD}{\rightarrow}$= $\underset{AD}{\rightarrow}$ $\underset{AD}{\rightarrow}$+ $\underset{BC}{\rightarrow}$ $\underset{BC}{\rightarrow}$ vì $\underset{DC}{\rightarrow}$ $\underset{DC}{\rightarrow}$=− $\underset{CD}{\rightarrow}$ $\underset{CD}{\rightarrow}$

b) Vì $\underset{AB}{\rightarrow}$ $\underset{AB}{\rightarrow}$= $\underset{AD}{\rightarrow}$ $\underset{AD}{\rightarrow}$+ $\underset{DB}{\rightarrow}$ $\underset{DB}{\rightarrow}$và $\underset{AD}{\rightarrow}$ $\underset{AD}{\rightarrow}$= $\underset{AC}{\rightarrow}$ $\underset{AC}{\rightarrow}$+ $\underset{CD}{\rightarrow}$ $\underset{CD}{\rightarrow}$ nên $\underset{AB}{\rightarrow}$ $\underset{AB}{\rightarrow}$= $\underset{AC}{\rightarrow}$ $\underset{AC}{\rightarrow}$+ $\underset{CD}{\rightarrow}$ $\underset{CD}{\rightarrow}$+ $\underset{BD}{\rightarrow}$ $\underset{BD}{\rightarrow}$

Do đó: 2 $\underset{AB}{\rightarrow}$ $\underset{AB}{\rightarrow}$= $\underset{AC}{\rightarrow}$ $\underset{AC}{\rightarrow}$+ $\underset{AD}{\rightarrow}$ $\underset{AD}{\rightarrow}$+ $\underset{CD}{\rightarrow}$ $\underset{CD}{\rightarrow}$+2 $\underset{DB}{\rightarrow}$ $\underset{DB}{\rightarrow}$

Vậy $\underset{AB}{\rightarrow}$ $\underset{AB}{\rightarrow}$=1/2 $\underset{AC}{\rightarrow}$ $\underset{AC}{\rightarrow}$+1/2 $\underset{AD}{\rightarrow}$ $\underset{AD}{\rightarrow}$+1/2 $\underset{CD}{\rightarrow}$ $\underset{CD}{\rightarrow}$+ $\underset{DB}{\rightarrow}$ $\underset{DB}{\rightarrow}$

Bài 3.7 trang 102 sách bài tập (SBT) – Hình học 12

ho hình tứ diện ABCD. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AC, BD, AD, BC. Chứng minh rằng:

a) $\underset{AB}{\rightarrow}$ $\underset{AB}{\rightarrow}$+ $\underset{CD}{\rightarrow}$ $\underset{CD}{\rightarrow}$= $\underset{AD}{\rightarrow}$ $\underset{AD}{\rightarrow}$+ $\underset{CB}{\rightarrow}$ $\underset{CB}{\rightarrow}$=2 $\underset{MN}{\rightarrow}$ $\underset{MN}{\rightarrow}$

b) $\underset{AB}{\rightarrow}$ $\underset{AB}{\rightarrow}$− $\underset{CD}{\rightarrow}$ $\underset{CD}{\rightarrow}$= $\underset{AC}{\rightarrow}$ $\underset{AC}{\rightarrow}$− $\underset{BD}{\rightarrow}$ $\underset{BD}{\rightarrow}$=2 $\underset{PQ}{\rightarrow}$ $\underset{PQ}{\rightarrow}$

Hướng dẫn làm bài:

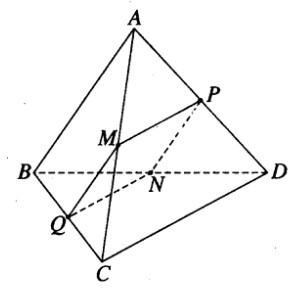
a) Ta có MPNQ là hình bình hành vì

$\underset{MP}{\rightarrow}$ $\underset{MP}{\rightarrow}$= $\underset{QN}{\rightarrow}$ $\underset{QN}{\rightarrow}$=1/2 $\underset{CD}{\rightarrow}$ $\underset{CD}{\rightarrow}$ và $\underset{QN}{\rightarrow}$ $\underset{QN}{\rightarrow}$=PN^→=1/2 $\underset{AB}{\rightarrow}$ $\underset{AB}{\rightarrow}$.

Do đó $\underset{MN}{\rightarrow}$ $\underset{MN}{\rightarrow}$=MQ^→+ $\underset{MP}{\rightarrow}$ $\underset{MP}{\rightarrow}$= $\underset{AB}{\rightarrow}$ $\underset{AB}{\rightarrow}$/2+ $\underset{CD}{\rightarrow}$ $\underset{CD}{\rightarrow}$/2 hay 2 $\underset{MN}{\rightarrow}$ $\underset{MN}{\rightarrow}$= $\underset{AB}{\rightarrow}$ $\underset{AB}{\rightarrow}$+ $\underset{CD}{\rightarrow}$ $\underset{CD}{\rightarrow}$ (1)

Mặt khác $\underset{AB}{\rightarrow}$ $\underset{AB}{\rightarrow}$= $\underset{AD}{\rightarrow}$ $\underset{AD}{\rightarrow}$+ $\underset{DB}{\rightarrow}$ $\underset{DB}{\rightarrow}$

$\underset{CD}{\rightarrow}$ $\underset{CD}{\rightarrow}$= $\underset{CB}{\rightarrow}$ $\underset{CB}{\rightarrow}$+ $\underset{BD}{\rightarrow}$ $\underset{BD}{\rightarrow}$

Nên $\underset{AB}{\rightarrow}$ $\underset{AB}{\rightarrow}$+ $\underset{CD}{\rightarrow}$ $\underset{CD}{\rightarrow}$= $\underset{AD}{\rightarrow}$ $\underset{AD}{\rightarrow}$+ $\underset{CB}{\rightarrow}$ $\underset{CB}{\rightarrow}$ (2)

Vì $\underset{BD}{\rightarrow}$ $\underset{BD}{\rightarrow}$= $\underset{BD}{\rightarrow}$ $\underset{BD}{\rightarrow}$

Từ (1) và (2) ta có: $\underset{AB}{\rightarrow}$ $\underset{AB}{\rightarrow}$+ $\underset{CD}{\rightarrow}$ $\underset{CD}{\rightarrow}$= $\underset{AD}{\rightarrow}$ $\underset{AD}{\rightarrow}$+ $\underset{CB}{\rightarrow}$ $\underset{CB}{\rightarrow}$=2 $\underset{MN}{\rightarrow}$ $\underset{MN}{\rightarrow}$ là đẳng thức cần chứng minh.

b) Ta có: $\underset{PQ}{\rightarrow}$ $\underset{PQ}{\rightarrow}$= $\underset{MQ}{\rightarrow}$ $\underset{MQ}{\rightarrow}$- $\underset{MP}{\rightarrow}$ $\underset{MP}{\rightarrow}$= $\underset{AB}{\rightarrow}$ $\underset{AB}{\rightarrow}$/2 - $\underset{CD}{\rightarrow}$ $\underset{CD}{\rightarrow}$/2

Do đó: 2 $\underset{PQ}{\rightarrow}$ $\underset{PQ}{\rightarrow}$= $\underset{AB}{\rightarrow}$ $\underset{AB}{\rightarrow}$− $\underset{CD}{\rightarrow}$ $\underset{CD}{\rightarrow}$ (3)

Mặt khác: $\underset{AB}{\rightarrow}$ $\underset{AB}{\rightarrow}$= $\underset{AC}{\rightarrow}$ $\underset{AC}{\rightarrow}$+ $\underset{CB}{\rightarrow}$ $\underset{CB}{\rightarrow}$

$\underset{CD}{\rightarrow}$ $\underset{CD}{\rightarrow}$= $\underset{BD}{\rightarrow}$ $\underset{BD}{\rightarrow}$− $\underset{BC}{\rightarrow}$ $\underset{BC}{\rightarrow}$

Nên $\underset{AB}{\rightarrow}$ $\underset{AB}{\rightarrow}$− $\underset{CD}{\rightarrow}$ $\underset{CD}{\rightarrow}$= $\underset{AC}{\rightarrow}$ $\underset{AC}{\rightarrow}$− $\underset{BD}{\rightarrow}$ $\underset{BD}{\rightarrow}$ (4)

Vì $\underset{CB}{\rightarrow}$ $\underset{CB}{\rightarrow}$− $\underset{(BC)}{\rightarrow}$ $\underset{(BC)}{\rightarrow}$= $\underset{0}{\rightarrow}$ $\underset{0}{\rightarrow}$

Từ (3) và (4) ta suy ra $\underset{AB}{\rightarrow}$ $\underset{AB}{\rightarrow}$− $\underset{CD}{\rightarrow}$ $\underset{CD}{\rightarrow}$= $\underset{AC}{\rightarrow}$ $\underset{AC}{\rightarrow}$− $\underset{BD}{\rightarrow}$ $\underset{BD}{\rightarrow}$=2 $\underset{PQ}{\rightarrow}$ $\underset{PQ}{\rightarrow}$ là đẳng thức cần chứng minh.

Bài 3.8 trang 102 sách bài tập (SBT) – Hình học 12

Trong không gian cho ba vecto tùy ý $\underset{a}{\rightarrow}$ $\underset{a}{\rightarrow}$, $\underset{b}{\rightarrow}$ $\underset{b}{\rightarrow}$, $\underset{c}{\rightarrow}$ $\underset{c}{\rightarrow}$. Gọi $\underset{u}{\rightarrow}$ $\underset{u}{\rightarrow}$= $\underset{a}{\rightarrow}$ $\underset{a}{\rightarrow}$−2 $\underset{b}{\rightarrow}$ $\underset{b}{\rightarrow}$, $\underset{v}{\rightarrow}$ $\underset{v}{\rightarrow}$=3 $\underset{b}{\rightarrow}$ $\underset{b}{\rightarrow}$− $\underset{c}{\rightarrow}$ $\underset{c}{\rightarrow}$, $\underset{w}{\rightarrow}$ $\underset{w}{\rightarrow}$=2 $\underset{c}{\rightarrow}$ $\underset{c}{\rightarrow}$−3 $\underset{a}{\rightarrow}$ $\underset{a}{\rightarrow}$.

Chứng tỏ rằng ba vecto $\underset{u}{\rightarrow}$ $\underset{u}{\rightarrow}$, $\underset{v}{\rightarrow}$ $\underset{v}{\rightarrow}$, $\underset{w}{\rightarrow}$ $\underset{w}{\rightarrow}$ đồng phẳng.

Hướng dẫn làm bài:

Muốn chứng tỏ rằng ba vecto $\underset{u}{\rightarrow}$ $\underset{u}{\rightarrow}$, $\underset{v}{\rightarrow}$ $\underset{v}{\rightarrow}$, $\underset{w}{\rightarrow}$ $\underset{w}{\rightarrow}$ đồng phẳng ta cần tìm hai số thực p và q sao cho $\underset{w}{\rightarrow}$ $\underset{w}{\rightarrow}$=p $\underset{u}{\rightarrow}$ $\underset{u}{\rightarrow}$+q $\underset{v}{\rightarrow}$ $\underset{v}{\rightarrow}$.

Giả sử có $\underset{w}{\rightarrow}$ $\underset{w}{\rightarrow}$=p $\underset{u}{\rightarrow}$ $\underset{u}{\rightarrow}$+q $\underset{v}{\rightarrow}$ $\underset{v}{\rightarrow}$

2c^→−3 $\underset{a}{\rightarrow}$ $\underset{a}{\rightarrow}$=p( $\underset{a}{\rightarrow}$ $\underset{a}{\rightarrow}$−2b^→)+q(3 $\underset{a}{\rightarrow}$ $\underset{a}{\rightarrow}$− $\underset{c}{\rightarrow}$ $\underset{c}{\rightarrow}$)

⇔ (3+p) $\underset{a}{\rightarrow}$ $\underset{a}{\rightarrow}$+(3q−2p) $\underset{b}{\rightarrow}$ $\underset{b}{\rightarrow}$−(q+2) $\underset{c}{\rightarrow}$ $\underset{c}{\rightarrow}$= $\underset{0}{\rightarrow}$ $\underset{0}{\rightarrow}$ (1)

Vì ba vecto lấy tùy ý $\underset{a}{\rightarrow}$ $\underset{a}{\rightarrow}$, $\underset{b}{\rightarrow}$ $\underset{b}{\rightarrow}$, $\underset{c}{\rightarrow}$ $\underset{c}{\rightarrow}$ nên đẳng thức (1) xảy ra khi và chỉ khi:

{3+p=0;3q−2p=0;q+2=0⇒p=−3;q=−2

Như vậy ta có: $\underset{w}{\rightarrow}$ $\underset{w}{\rightarrow}$=−3 $\underset{u}{\rightarrow}$ $\underset{u}{\rightarrow}$−2 $\underset{v}{\rightarrow}$ $\underset{v}{\rightarrow}$ nên ba vecto $\underset{u}{\rightarrow}$ $\underset{u}{\rightarrow}$, v^→, $\underset{w}{\rightarrow}$ $\underset{w}{\rightarrow}$ đồng phẳng.

Bài 3.9 trang 103 sách bài tập (SBT) – Hình học 12

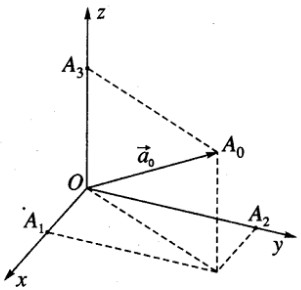
Trong không gian Oxyz cho một vecto $\underset{a}{\rightarrow}$ $\underset{a}{\rightarrow}$ tùy ý khác vecto $\underset{0}{\rightarrow}$ $\underset{0}{\rightarrow}$. Gọi α,β,γ là ba góc tạo bởi ba vecto đơn vị $\underset{i}{\rightarrow}$ $\underset{i}{\rightarrow}$, $\underset{j}{\rightarrow}$ $\underset{j}{\rightarrow}$, $\underset{k}{\rightarrow}$ $\underset{k}{\rightarrow}$ trên ba trục Ox, Oy, Oz và vecto $\underset{a}{\rightarrow}$ $\underset{a}{\rightarrow}$. Chứng minh rằng: cos²α+cos²β+cos²γ=1

Hướng dẫn làm bài:

Giải SBT Toán 12 bài 1: Hệ tọa độ trong không gian

Bài 3.10 trang 103 sách bài tập (SBT) – Hình học 12

Cho hình tứ diện ABCD.

a) Chứng minh hệ thức:

$\underset{AB}{\rightarrow}$ $\underset{AB}{\rightarrow}$. $\underset{CD}{\rightarrow}$ $\underset{CD}{\rightarrow}$+ $\underset{AC}{\rightarrow}$ $\underset{AC}{\rightarrow}$. $\underset{DB}{\rightarrow}$ $\underset{DB}{\rightarrow}$+ $\underset{AD}{\rightarrow}$ $\underset{AD}{\rightarrow}$. $\underset{BC}{\rightarrow}$ $\underset{BC}{\rightarrow}$=0

b) Từ hệ thức trên hãy suy ra định lí: “Nếu một hình tứ diện có hai cặp cạnh đối diện vuông góc với nhau thì cặp cạnh đối diện thứ ba cũng vuông góc với nhau.”

Hướng dẫn làm bài:

a) Ta có

$\underset{AB}{\rightarrow}$ $\underset{AB}{\rightarrow}$. $\underset{CD}{\rightarrow}$ $\underset{CD}{\rightarrow}$= $\underset{AB}{\rightarrow}$ $\underset{AB}{\rightarrow}$( $\underset{AD}{\rightarrow}$ $\underset{AD}{\rightarrow}$− $\underset{AC}{\rightarrow}$ $\underset{AC}{\rightarrow}$)= $\underset{AB}{\rightarrow}$ $\underset{AB}{\rightarrow}$. $\underset{AD}{\rightarrow}$ $\underset{AD}{\rightarrow}$− $\underset{AB}{\rightarrow}$ $\underset{AB}{\rightarrow}$. $\underset{AC}{\rightarrow}$ $\underset{AC}{\rightarrow}$ (1)

$\underset{AC}{\rightarrow}$ $\underset{AC}{\rightarrow}$. $\underset{DB}{\rightarrow}$ $\underset{DB}{\rightarrow}$= $\underset{AC}{\rightarrow}$ $\underset{AC}{\rightarrow}$( $\underset{AB}{\rightarrow}$ $\underset{AB}{\rightarrow}$− $\underset{AD}{\rightarrow}$ $\underset{AD}{\rightarrow}$)= $\underset{AC}{\rightarrow}$ $\underset{AC}{\rightarrow}$. $\underset{AB}{\rightarrow}$ $\underset{AB}{\rightarrow}$− $\underset{AC}{\rightarrow}$ $\underset{AC}{\rightarrow}$. $\underset{AD}{\rightarrow}$ $\underset{AD}{\rightarrow}$ (2)

$\underset{AD}{\rightarrow}$ $\underset{AD}{\rightarrow}$. $\underset{BC}{\rightarrow}$ $\underset{BC}{\rightarrow}$= $\underset{AD}{\rightarrow}$ $\underset{AD}{\rightarrow}$( $\underset{AC}{\rightarrow}$ $\underset{AC}{\rightarrow}$− $\underset{AB}{\rightarrow}$ $\underset{AB}{\rightarrow}$)= $\underset{AD}{\rightarrow}$ $\underset{AD}{\rightarrow}$. $\underset{AC}{\rightarrow}$ $\underset{AC}{\rightarrow}$− $\underset{AD}{\rightarrow}$ $\underset{AD}{\rightarrow}$. $\underset{AB}{\rightarrow}$ $\underset{AB}{\rightarrow}$ (3)

Lấy (1) + (2) + (3) ta có hệ thức cần chứng minh là:

$\underset{AB}{\rightarrow}$ $\underset{AB}{\rightarrow}$. $\underset{CD}{\rightarrow}$ $\underset{CD}{\rightarrow}$+ $\underset{AC}{\rightarrow}$ $\underset{AC}{\rightarrow}$. $\underset{DB}{\rightarrow}$ $\underset{DB}{\rightarrow}$+ $\underset{AD}{\rightarrow}$ $\underset{AD}{\rightarrow}$. $\underset{BC}{\rightarrow}$ $\underset{BC}{\rightarrow}$=0

b) Từ hệ thức trên ta suy ra định lí: “Nếu tứ diện ABCD có AB⊥CD,AC⊥DB, nghĩa là $\underset{AB}{\rightarrow}$ $\underset{AB}{\rightarrow}$. $\underset{CD}{\rightarrow}$ $\underset{CD}{\rightarrow}$=0 và $\underset{AC}{\rightarrow}$ $\underset{AC}{\rightarrow}$. $\underset{DB}{\rightarrow}$ $\underset{DB}{\rightarrow}$=0 thì $\underset{AD}{\rightarrow}$ $\underset{AD}{\rightarrow}$. $\underset{BC}{\rightarrow}$ $\underset{BC}{\rightarrow}$= 0 và do đó AD⊥BC.”

---------------------------------

Trên đây VnDoc.com đã giới thiệu tới bạn đọc tài liệu: Giải SBT Toán 12 bài 1: Hệ tọa độ trong không gian. Để có kết quả cao hơn trong học tập, VnDoc xin giới thiệu tới các bạn học sinh tài liệu Giải bài tập Toán lớp 12, Giải bài tập Hóa học lớp 12, Giải bài tập Vật Lí 12 mà VnDoc tổng hợp và đăng tải.

Chia sẻ, đánh giá bài viết

1

314

Bài trước

Bài sau