Bài tập nâng cao Toán lớp 5: Diện tích hình tam giác
Bài tập Toán lớp 5 nâng cao: Diện tích hình tam giác
Bài tập nâng cao Toán lớp 5: Diện tích hình tam giác được VnDoc biên soạn bao gồm đáp án chi tiết cho từng bài tập giúp các em học sinh luyện tập các dạng bài tập hình học - hình tam giác. Qua đó giúp các em học sinh ôn tập, củng cố và nâng cao thêm kiến thức đã học trong chương trình Toán lớp 5, Mời các em học sinh và quý thầy cô cùng tham khảo chi tiết.
Bài tập Toán lớp 5 nâng cao: Diện tích hình tam giác
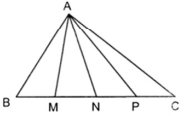
Bài 1: Cho hình tam giác ABC và BM = MN = NP = PC (như hình vẽ). Tính tỉ số diện tích của hình tam giác AMC và diện tích hình tam giác ABC.
Bài 2: Một hình tam giác có độ dài đáy gấp đôi chiều cao và có diện tích 4m2. Tính chiều cao của hình tam giác theo đơn vị đề-xi-mét.
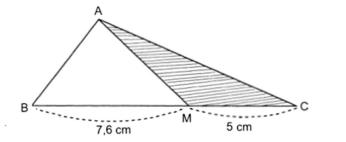
Bài 3: Tính diện tích hình tam giác ABM (như hình vẽ) biết diện tích hình tam giác AMC là 34cm².
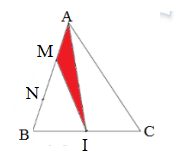
Bài 4: Trong tam giác ABC, cạnh AB chia thành 3 phần bằng nhau, cạnh BC chia thành 2 phần bằng nhau. Tính diện tích phần màu đỏ biết diện tích tam giác ABC bằng 72cm².
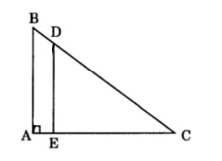
Bài 5: Một mảnh đất hình tam giác ABC vuông tại A, cạnh AB dài 40m, cạnh AC dài 80m. Để mở rộng giao thông người ta đắp con đường rộng 4m chạy dọc theo cạnh AB (như hình vẽ). Tính diện tích còn lại của mảnh đất.
Bài 6: Một mảnh đất hình tam giác MNP vuông tại M, cạnh MN dài 15m, cạnh MP dài 20m. Người ta đắp một con đường chạy dọc theo cạnh MN rộng 4m (như hình vẽ). Tính diện tích còn lại của mảnh đất.
Bài 7: Cho hình tam giác ABC có BM = MC, AD = DE = EM
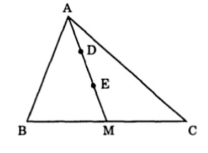
a, Ghi tên tất cả các hình tam giác có chung đỉnh A và tính diện tích của từng hình tam giác đó, biết rằng diện tích tam giác BEC = 420cm2.
b, Kéo dài đoạn BE cho cắt cạnh AC ở điểm N. Hỏi M có là điểm chính giữa cạnh AC không? Vì sao?
Bài 8: Cho hình vẽ dưới đây. Tính diện tích tam giác ABC.
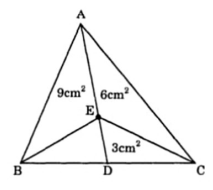
Bài 9: Một hình tam giác ABC có cạnh đáy 3,5m. Nếu kéo dài cạnh đáy BC thêm 2,2m thì diện tích tam giác tăng thêm 5,5 m2. Tính diện tích hình tam giác ABC đó?
Bài 10: Một tấm bảng quảng cáo hình tam giác có tổng cạnh đáy và chiều cao là 28m, cạnh đáy hơn chiều cao 14m. Tính diện tích tấm bảng quảng cáo đó?
Bài 11: Cho tam giác ABC vuông góc tại A, chu vi là 93cm. Cạnh AB bằng 
\(\frac{4}{3}\) cạnh AC, cạnh BC bằng \(\frac{5}{3}\) cạnh AC. Tính diện tích hình tam giác ABC ?
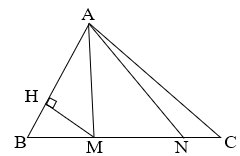
Bài 12: Tính diện tích tam giác ABC biết MH = 24 cm, AB = 50 cm.
Đoạn thẳng BM = \(\frac{2}{3}\)đoạn thẳng MN, đoạn thẳng NC = \(\frac{1}{2}\) đoạn thẳng MN.
Hướng dẫn giải bài tập
Bài 1:
Gọi AH là chiều cao của tam giác ABC. Suy ra AH cũng là chiều cao của các tam giác AMC
Có BC = BM + MN + NP + PC = PC + PC + PC + PC = 4xPC (vì BM = MN = NP = PC)
Có MC = MN + NP + PC = PC + PC + PC = 3 x PC (vì MN = NP = PC)
Diện tích tam giác ABC là: (AH x BC) / 2 = (AH x 4 x PC) / 2
Diện tích tam giác AMC là: (AH x MC) / 2 = (AH x 3 x PC) / 2
Tỉ số diện tích tam giác AMC và tam giác ABC là:
\(\frac{{{S_{AMC}}}}{{{S_{ABC}}}} = \frac{{AH \times PC \times 3}}{2}:\frac{{AH \times PC \times 4}}{2} = \frac{{AH \times PC \times 3}}{2} \times \frac{2}{{AH \times PC \times 4}} = \frac{3}{4}\)
Mời các bạn tải về để xem tiếp nội dung cùng đáp án.
-----------
Tham khảo:
