Giải SBT Toán 12 bài tập ôn tập cuối năm - Giải Tích 12

Bài tập ôn tập cuối năm - Giải Tích 12

VnDoc xin giới thiệu tới bạn đọc tài liệu Giải SBT Toán 12 bài tập ôn tập cuối năm - Giải Tích 12, chắc chắn nội dung tài liệu sẽ là nguồn thông tin hay để giúp các bạn học sinh có kết quả cao hơn trong học tập. Mời các bạn học sinh tham khảo.

Giải SBT Toán 12 bài tập ôn tập cuối năm

Bài 5.1 trang 219 sách bài tập (SBT) - Giải tích 12

a) Xác định a, b, c, d để đồ thị của các hàm số:

y = x² + ax + b và y = cx + d

cùng đi qua hai điểm M(1; 1) và B(3; 3).

b) Vẽ đồ thị của các hàm số ứng với các giá trị a, b, c và d tìm được trên cùng một mặt phẳng tọa độ. Tính diện tích của hình phẳng giới hạn bởi hai đường cong trên.

c) Tính thể tích của vật thể tròn xoay sinh bởi hình phẳng trên quay quanh trục hoành.

Hướng dẫn làm bài

a) a và b thỏa mãn hệ phương trình:

\(\left\{\begin{matrix} 1 + a + b = 1 \\ 9 + 3 a + b = 3 \end{matrix}\right.\) ⇒ \(\left\{\begin{matrix} a + b = 0 \\ 3 a + b = - 6 \end{matrix}\right.\) ⇔ \(\left\{\begin{matrix} a = - 3 \\ b = 3 \end{matrix}\right.\)

c và d thỏa mãn hệ phương trình:

\(\left\{\begin{matrix} c + d = 1 \\ 3 c + d = 3 \end{matrix}\right.\) ⇒ \(\left\{\begin{matrix} c = 1 \\ d = 0 \end{matrix}\right.\)

b) (H.90) Ta có hai hàm số tương ứng là: y = x² – 3x + 3 và y = x

Vậy S=³∫₁(−x²+4x−3)dx=4/3 (đơn vị diện tích)

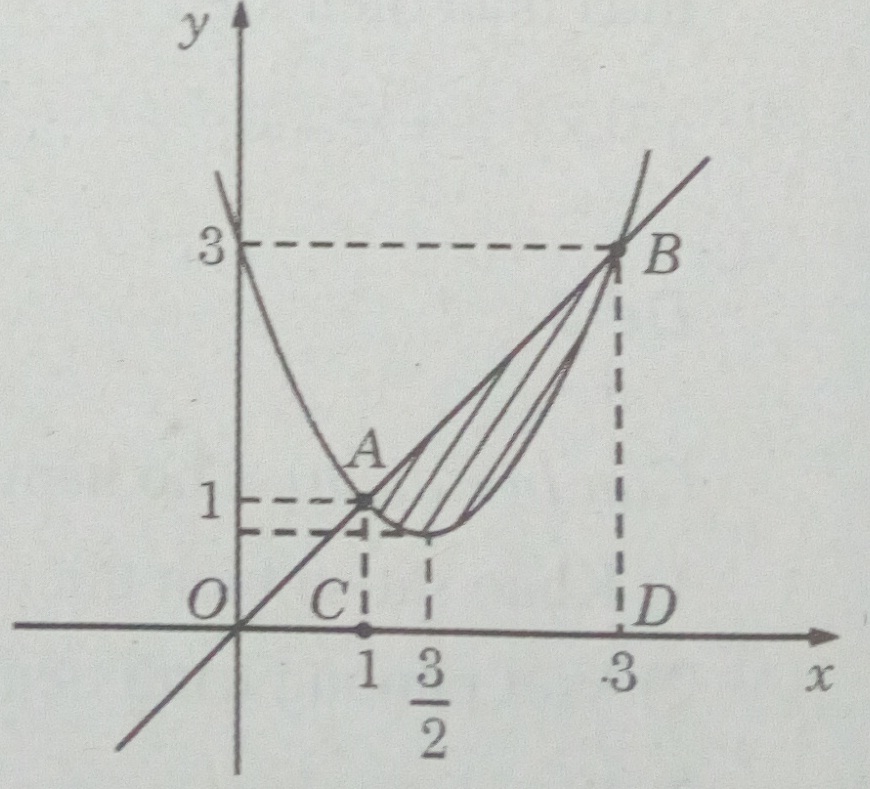
c) V = V₁ – V₂, trong đó V1 là thể tích vật thể tròn xoay sinh ra do quay hình thang ACDB quanh trục Ox, V₂ là thể tích vật thể tròn xoay sinh ra do quay hình thang cong ACDB quanh trục Ox.

Ta có V₁=π³∫₁x²dx=26/3π

V₂=π³∫₁(x²−3x+3)²dx=22/5π

Vậy V=26/3π−22/5π=64/15π (đơn vị thể tích)

Bài 5.2 trang 219 sách bài tập (SBT) - Giải tích 12

a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số: y=−x+2/x+2

b) Viết phương trình tiếp tuyến của (C), biết nó vuông góc với đường thẳng y=1/4x−42

Hướng dẫn làm bài

a) y=−x+2/x+2

+) Tập xác định: D = R\{-2}

+) Ta có: y′=−4/(x+2)²

Bảng biến thiên:

Hàm số nghịch biến trên các khoảng (−∞;−2),(−2;+∞)

+) Tiệm cận đứng x = -2 vì lim_x→−2+y=+∞,lim_x→−2−y=−∞

Tiệm cận ngang y = -1 vì lim_x→±∞y=−1

Giao với các trục tọa độ: (0; 1); (2; 0)

Đồ thị

b) Tiếp tuyến của đồ thị có hệ số góc k = -4 (vì vuông góc với đường thẳng y=1/4x−42)

Hoành độ tiếp điểm thỏa mãn phương trình:

−4/(x+2)²=−4=>[x₁=−3;x₂=−1

Ứng với x₁=−3, ta có tiếp tuyến y = - 4x – 17

Ứng với x₂=−1, ta có tiếp tuyến y = - 4x – 1.

Bài 5.3 trang 219 sách bài tập (SBT) - Giải tích 12

a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số: y=4x−5/x−1

b) Tính diện tích hình phẳng giới hạn bởi (C), tiếp tuyến của (C) tại A(2; 3) và đường thẳng x = 4.

Hướng dẫn làm bài

a) Tập xác định: D = R\{1}

Đạo hàm: y′=1/(x−1)²

Bảng biến thiên:

Các khoảng đồng biến là (−∞;1) và (1;+∞):

Tiệm cận đứng x = 1 vì lim_x→1+y=−∞;lim_x→1−y=+∞

Tiệm cận ngang y = 4 vì lim_x→±∞y=4

Giao với các trục tọa độ: (0; 5) và (5/4;0)

Đồ thị

b) Ta có: y’(2) = 1. Phương trình tiếp tuyến là y = x + 1

Diện tích của miền cần tìm là:

S=⁴∫₂(x+1−4+1/x−1)dx=⁴∫₂(x−3+1/x−1)dx=ln3

Bài 5.4 trang 219 sách bài tập (SBT) - Giải tích 12

Tìm các đường tiệm cận của đồ thị các hàm số sau:

a) y=5x+3/−x+2

b) y=−6x+2/x−1

c) y=2x²+8x−9/3x²+x−4

d) y=x+2/−2x+5

Hướng dẫn làm bài

a) Tiệm cận đứng: x = 2; Tiệm cận ngang: y = -5

b) Tiệm cận đứng: x = 1; Tiệm cận ngang: y = -6

c) Ta có: lim_x→±∞2x²+8x−9/3x²+x−4=lim_x→±∞x²(2+8/x−9/x²)/x²(3+1/x−4/x²)=2/3

Vậy đồ thị có đường tiệm cận ngang y=2/3

Ta có y=2x²+8x+9/(x−1)(3x+4)

Từ đó đồ thị có hai tiệm cận đứng là x = 1 và x=−4/3

d) Tiệm cận đứng: x=5/2. Tiệm cận ngang: y=−1/2

Bài 5.5 trang 219 sách bài tập (SBT) - Giải tích 12

Tìm các điểm cực trị của các hàm số sau:

a) y=−x³−6x²+15x+1

b) y=x²√x²+2

c) y=x+ln(x+1)

d) y=x−1+1/x+1

Hướng dẫn làm bài

a) y′=−3x²−12x+15;y′′=−6x−12

y′=0⇔3x²+12x−15=0⇔[x=1;x=−5

y′′(1)=−18<0;y′′(−5)=18>0

Vậy với x = -5 hàm số đạt cực tiểu và y_CT = -99

Với x = 1 hàm số đạt cực đại và y_CĐ = 9

b) Tập xác định D = R. Hàm số có cực tiểu khi x = 0, yCT = 0

c) Tập xác định: x>−1;y′=1+1/x+1;y′>0,∀x>−1;

Hàm số luôn đồng biến nên không có cực trị.

d) Tập xác định: R\{-1};

y′=1−/1(x+1)²;y′=0⇔[x=0/x=−2

y′′=2/(x+1)³;y′′(0)=2>0′y′′(−2)=−2<0

Hàm số đạt cực đại tại x = -2 và y_CĐ = - 4

Hàm số đạt cực tiểu tại x = 0 và y_CT = 0

Bài 5.6 trang 219 sách bài tập (SBT) - Giải tích 12

Tìm a∈(0;2π) để hàm số y=1/3x³−1/2(1+2cosa)x²+2xcosa+1 đồng biến trên khoảng (1;+∞)(1;+∞).

Hướng dẫn làm bài

Tập xác định: D = R; y′=x²−(1+2cosa)x+2cosa

y′=0⇔[x=1;x=2cosa

Vì y’ > 0 ở ngoài khoảng nghiệm nên để hàm số đồng biến với mọi x > 1 thì 2cosa≤1⇔cosa≤1/2⇒π/3≤a≤5π/3 (vì a∈(0;2π).

Bài 5.7 trang 220 sách bài tập (SBT) - Giải tích 12

Chứng minh các bất đẳng thức sau:

a) e^x+cosx≥2+x−x²/2,∀x∈R

b) e^x−e^−x≥2ln(x+√1+x²),∀x≥0

c) 8sin²x/2+sin2x>2x,∀x∈(0;π]

Hướng dẫn làm bài

a) Xét hàm số f(x)=e^x+cosx−2−x+x²/2, có tập xác định là R.

f′(x)=e^x−sinx−1+x;f′(x)=0⇔x=0

Ta lại có f′′(x)=e^x+1−cosx>0,∀x vì 1−cosx≥0 và e^x>0

Như vậy, f’(x) đồng biến trên R. Từ đó: f′(x)<f′(0)=0,∀x<0;f′(x)>f′(0)=0,∀x>0

Ta có bảng biến thiên

Hàm số f(x)=e^x+cosx−2−x+x²/2≥f_CT=f(0)=0,∀x∈R

Từ đó suy ra điều phải chứng minh.

b) ∀x≥0∀x≥0 xét hàm số f(x)=e^x−e^−x−2ln(x+√1+x²), ta có

f′(x)=e^x+e^−x−2/√1+x²

Từ đó f ‘(x) > 0 với mọi x > 0 (vì e^x+e^−x>2 và 2/√1+x²<2 và f‘(x)=0⇔x=0

Vậy f(x) đồng biến trên [0;+∞), tức là:

f(x)≥f(0)=e⁰−e⁰−2ln1=0

Từ đó suy ra điều cần chứng minh

c) Xét hàm số f(x)=8sin²x/2+sin2x−2x,∀x∈(0;π]

f′(x)=4sinx+2cos2x−2=4sinx(1−sinx)

f′(x)=0⇔[x=π/2;x=π

Với x∈(0;π] ta có f′(x)≥0 và dấu bằng chỉ xảy ra tại hai điểm.

Vậy f(x) đồng biến trên nửa (0;π]. Mặt khác, f(0) = 0 nên f(x) > 0.

Từ đó suy ra điều phải chứng minh.

Bài 5.8 trang 220 sách bài tập (SBT) - Giải tích 12

Tìm giá trị lớn nhất và nhỏ nhất của các hàm số sau trên các khoảng, đoạn tương ứng:

a) g(x) = |x³ + 3x² – 72x + 90| trên đoạn [-5; 5]

b) f(x) = x⁴ – 4x² + 1 trên đoạn [-1; 2]

c) f(x) = x – ln x + 3 trên khoảng (0;+∞)

Hướng dẫn làm bài

a) Xét hàm số f(x)=x³+3x²−72x+90 trên đoạn [-5; 5]

f′(x)=3x²+6x−72;f′(x)=0⇔[x=4;x=−6∉[−5;5]

f(−5)=400;f(5)=−70;f(4)=−86

Ngoài ra, f(x) liên tục trên đoạn [-5; 5] và f(−5).f(5)<0 nên tồn tại x₀∈(−5;5) sao cho f(x0)=0

Ta có g(x)=|f(x)|≥0 và g(x₀)=|f(x₀)|=0;g(−5)=|400|=400

g(5)=|−70|=70;g(4)=|f(4)|=|−86|=86

Vậy ming(x)_[−5;5]=g(x₀)=0;maxg(x)_[−5;5]=g(−5)=400

b) minf(x)_[−1;2]=f(√2)=−3;maxf(x)_[−1;2]=f(2)=f(0)=1

c) minf(x)_(0;+∞)=f(1)=4. Không có giá trị lớn nhất.

Bài 5.9 trang 220 sách bài tập (SBT) - Giải tích 12

Cho hàm số y=1/3x³−(m−1)x²+(m−3)x+4.1/2 (m là tham số) (1)

a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số (1) khi m = 0.

b) Viết phương trình của tiếp tuyến với đồ thị (C) tại điểm A(0;4.1/2)

c) Tính diện tích hình phẳng giới hạn bởi (C), trục hoành và các đường thẳng x = 0 và x = 2.

d) Xác định m để đồ thị của (1) cắt đường thẳng y=−3x+4.1/2 tại ba điểm phân biệt.

Hướng dẫn làm bài:

a) y=1/3x³+x²−3x+4.1/2

+) Tập xác định: D = R

+) Sự biến thiên: y’ = x² + 2x – 3

y′=0⇔[x=1;x=−3

Bảng biến thiên:

Hàm số đồng biến trên các khoảng (-∞; -3) và (1; +∞), nghịch biến trên khoảng (-3; 1).

Hàm số đạt cực đại tại x=−3;y_CD=13.1/2;y_CT=2.5/6x=−3; khi x = 1

Đồ thị cắt trục tung tại điểm (0;4.1/2) và có dạng như hình dưới đây.

y′′=2x+2;y′′=0⇔x=−1. Vậy là tâm đối xứng của đồ thị.

b) Tiếp tuyến với (C) đi qua A(0;4.1/2) có phương trình là:y=f′(0)x+4.1/2, trong đó f(x)=1/3x³+x²−3x+4.1/2

Ta có f ’(0) = -3.

Vậy phương trình tiếp tuyến là y=−3x+4.1/2

c) S=²∫₀(1/3x³+x²−3x+4.1/2)dx=7 (đơn vị diện tích).

d) Hoành độ giao điểm của đường thẳng y=−3x+4.1/2 với đồ thị của (1) thỏa mãn phương trình

1/3x³−(m−1)x²+(m−3)x+4.1/2=−3x+4.1/2 (2)

Ta có (2)⇔1/3x³−(m−1)x²+mx=0

⇔x[x²−3(m−1)x+3m]=0

Để (2) có ba nghiệm phân biệt thì phương trình f(x) = x²– 3(m – 1)x + 3m = 0 phải có hai nghiệm phân biệt khác 0, tức là:

Bài 5.10 trang 220 sách bài tập (SBT) - Giải tích 12

a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số y=4x+4/2x+1

b) Từ (C) suy ra đồ thị của hàm số y=|4x+4/2x+1|

c) Viết phương trình tiếp tuyến với (C) , biết rằng tiếp tuyến đó song song với đường thẳng y=−1/4x−3

Hướng dẫn làm bài:

a) y=4x+4/2x+1

Tập xác định: D=R∖{−1/2}

Ta có y′=−4/(2x+1)²

Bảng biến thiên:

Hàm số nghịch biến trên các khoảng (−∞;−12) và (−12;+∞)

Tiệm cận đứng: x=−1/2; Tiệm cận ngang: y = 2

Giao với các trục tọa độ: (0; 4) và (-1; 0)

Đồ thị:

b) Đồ thị của hàm số được suy ra từ (C) bằng cách giữ nguyên phần đồ thị nằm phía trên trục hoành và lấy đối xứng qua trục hoành phần đồ thị nằm phía dưới trục hoành.

c) Tiếp tuyến có hệ số góc bằng −1/4

Hoành độ tiếp điểm phải thỏa mãn phương trình −4/(2x+1)²=−1/4

⇔(2x+1)²=16⇔ x=−5/2;x=3/2

Hai tiếp tuyến cần tìm là y=−1/4x+7/8 và y=−1/4x+23/8

---------------------------------

Trên đây VnDoc.com đã giới thiệu tới bạn đọc tài liệu: Giải SBT Toán 12 bài tập ôn tập cuối năm - Giải Tích 12. Để có kết quả cao hơn trong học tập, VnDoc xin giới thiệu tới các bạn học sinh tài liệu Giải bài tập Toán lớp 12, Giải bài tập Hóa học lớp 12, Giải bài tập Vật Lí 12 mà VnDoc tổng hợp và đăng tải.