Đề thi giữa học kì 2 lớp 6 môn Toán - Đề số 3

Đề thi giữa học kì 2 môn Toán lớp 6

Đề thi giữa học kì 2 môn Toán lớp 6 - Đề số 3

A. Đề ôn thi giữa học kì 2 môn Toán lớp 6
B. Lời giải đề ôn thi giữa học kì 2 môn Toán lớp 6

Đề thi giữa học kì 2 môn Toán lớp 6 - Đề 3 được đội ngũ giáo viên của VnDoc biên soạn sẽ giúp cho các em học sinh ôn tập, củng cố kiến thức trọng tâm chuẩn bị cho các bài thi kiểm tra giữa học kì 2 lớp 6. Mời các thầy cô cùng các em học sinh tham khảo chi tiết.

Đề thi giữa học kì 2 môn Toán lớp 6 - Đề 3 bao gồm các bài tập tự luận với các câu hỏi với mức độ từ cơ bản tới nâng cao, có đáp án chi tiết cho từng dạng bài tập, các em học sinh tham khảo ôn tập, rèn luyện kỹ năng giải Toán chuẩn bị cho bài thi giữa học kì lớp 6.

Đề ôn thi giữa học kì 2 môn Toán lớp 6 - Đề 3

A. Đề ôn thi giữa học kì 2 môn Toán lớp 6

Bài 1: Thực hiện các phép tính sau:

a, $\frac{{{2^5}.9 - {2^6}}}{{32.5 + {2^5}{{.3}^2}}}$ $\frac{{{2^5}.9 - {2^6}}}{{32.5 + {2^5}{{.3}^2}}}$ b, $56 - 6.\left( {\left| { - 17} \right| + 9} \right)$ $56 - 6.\left( {\left| { - 17} \right| + 9} \right)$

c, $\frac{{50.22 + 11.50}}{{50.11}}$ $\frac{{50.22 + 11.50}}{{50.11}}$ d, $\frac{7}{9}.\frac{9}{{16}} + \frac{7}{9}.\frac{{11}}{{16}} - \frac{7}{9}.\frac{1}{4}$ $\frac{7}{9}.\frac{9}{{16}} + \frac{7}{9}.\frac{{11}}{{16}} - \frac{7}{9}.\frac{1}{4}$

Bài 2: Tìm x, biết:

a, $\frac{1}{3}x + \frac{5}{6}x = \frac{{49}}{6}$ $\frac{1}{3}x + \frac{5}{6}x = \frac{{49}}{6}$ b, $20:\left( {24 + 2x} \right) = \frac{2}{3}$ $20:\left( {24 + 2x} \right) = \frac{2}{3}$

c, $\frac{x}{2} + \frac{x}{5} = \frac{{17}}{{10}} - \frac{2}{5} + \frac{5}{6}$ $\frac{x}{2} + \frac{x}{5} = \frac{{17}}{{10}} - \frac{2}{5} + \frac{5}{6}$

Bài 3: Tìm các số nguyên x, y, z thỏa mãn $\frac{x}{{ - 10}} = \frac{{ - 7}}{y} = \frac{z}{{ - 24}} = \frac{{ - 4}}{8}$ $\frac{x}{{ - 10}} = \frac{{ - 7}}{y} = \frac{z}{{ - 24}} = \frac{{ - 4}}{8}$

Bài 4: Trên cùng một nửa mặt phẳng bờ chứa tia Ox, vẽ hai góc $\widehat {xOy} = {128^0}$ $\widehat {xOy} = {128^0}$ và $\widehat {xOz} = {64^0}$ $\widehat {xOz} = {64^0}$

a, Trong 3 tia Ox, Oy, Oz, tia nào nằm giữa hai tia còn lại? Vì sao?

b, Tính số đo góc $\widehat {yOz}$ $\widehat {yOz}$

c, Tia Oz có là tia phân giác của góc xOy không? Vì sao?

d, Gọi Ot là tia đối của tia Oy. Tính số đo góc $\widehat {xOt}$ $\widehat {xOt}$

Bài 5: Chứng minh rằng $A > \frac{7}{{12}}$ $A > \frac{7}{{12}}$, biết

$A = \frac{1}{{31}} + \frac{1}{{32}} + \frac{1}{{33}} + ... + \frac{1}{{60}}$ $A = \frac{1}{{31}} + \frac{1}{{32}} + \frac{1}{{33}} + ... + \frac{1}{{60}}$

B. Lời giải đề ôn thi giữa học kì 2 môn Toán lớp 6

Bài 1:

a, $\frac{1}{2}$ $\frac{1}{2}$ b, -100 c, 3 d, $\frac{7}{9}$ $\frac{7}{9}$

Bài 2:

a, x = 7 b, x = 3 c, $x = \frac{{64}}{{21}}$ $x = \frac{{64}}{{21}}$

Bài 3: x = 5, y = 14, z = 12

Bài 4:

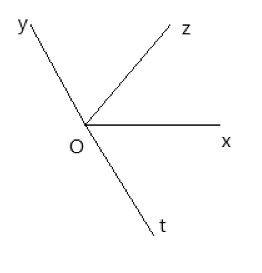
đề thi giữa học kì 2 môn toán lớp 6 đề số 3 ảnh số 1

a, Trên cùng một nửa mặt phẳng bờ chứa tia Ox, có $\widehat {xOy} > \widehat {xOz}\left( {12{8^0} > 6{4^0}} \right)$ $\widehat {xOy} > \widehat {xOz}\left( {12{8^0} > 6{4^0}} \right)$nên tia Oz nằm giữa hai tia Oy và Ox

b, Trên cùng một nửa mặt phẳng bờ chứa tia Ox, có tia Oz nằm giữa hai tia Oy và Ox nên ta có:

$\begin{array}{l} \widehat {xOz} + \widehat {zOy} = \widehat {xOy}\\ {64^0} + \widehat {zOy} = {128^0}\\ \Rightarrow \widehat {zOy} = 12{8^0} - 6{4^0} = 6{4^0} \end{array}$ $\begin{array}{l} \widehat {xOz} + \widehat {zOy} = \widehat {xOy}\\ {64^0} + \widehat {zOy} = {128^0}\\ \Rightarrow \widehat {zOy} = 12{8^0} - 6{4^0} = 6{4^0} \end{array}$

c, Trên cùng một nửa mặt phẳng bờ chứa tia Ox, có tia Oz nằm giữa hai tia Oy và Ox và $\widehat {zOy} = \widehat {zOx}\left( { = 6{4^0}} \right)$ $\widehat {zOy} = \widehat {zOx}\left( { = 6{4^0}} \right)$ nên tia Oz là tia phân giác của góc xOy

d, Vì Ot và Oy là hai tia đối nhau nên $\widehat {yOt} = {180^0}$ $\widehat {yOt} = {180^0}$

Có góc $\widehat {xOt}$ $\widehat {xOt}$ và $\widehat {x{\mathop{\rm Oy}\nolimits} }$ $\widehat {x{\mathop{\rm Oy}\nolimits} }$ là hai góc kề bù nên

$\begin{array}{l} \widehat {xOt} + \widehat {xOy} = 18{0^0}\\ \widehat {xOt} + 12{8^0} = 18{0^0}\\ \Rightarrow \widehat {xOt} = 18{0^0} - 12{8^0} = {52^0} \end{array}$ $\begin{array}{l} \widehat {xOt} + \widehat {xOy} = 18{0^0}\\ \widehat {xOt} + 12{8^0} = 18{0^0}\\ \Rightarrow \widehat {xOt} = 18{0^0} - 12{8^0} = {52^0} \end{array}$

Bài 5:

$\begin{array}{l} A = \frac{1}{{31}} + \frac{1}{{32}} + \frac{1}{{33}} + ... + \frac{1}{{60}}\\ = \left( {\frac{1}{{31}} + \frac{1}{{32}} + ... + \frac{1}{{44}} + \frac{1}{{45}}} \right) + \left( {\frac{1}{{46}} + \frac{1}{{47}} + ... + \frac{1}{{60}}} \right) \end{array}$ $\begin{array}{l} A = \frac{1}{{31}} + \frac{1}{{32}} + \frac{1}{{33}} + ... + \frac{1}{{60}}\\ = \left( {\frac{1}{{31}} + \frac{1}{{32}} + ... + \frac{1}{{44}} + \frac{1}{{45}}} \right) + \left( {\frac{1}{{46}} + \frac{1}{{47}} + ... + \frac{1}{{60}}} \right) \end{array}$

Xét $\frac{1}{{31}} + \frac{1}{{32}} + ... + \frac{1}{{44}} + \frac{1}{{45}}$ $\frac{1}{{31}} + \frac{1}{{32}} + ... + \frac{1}{{44}} + \frac{1}{{45}}$

Nhận thấy $\frac{1}{{31}} > \frac{1}{{45}};\frac{1}{{32}} > \frac{1}{{45}};...;\frac{1}{{44}} > \frac{1}{{45}}$ $\frac{1}{{31}} > \frac{1}{{45}};\frac{1}{{32}} > \frac{1}{{45}};...;\frac{1}{{44}} > \frac{1}{{45}}$và từ 31 đến 45 có 15 số

$\Rightarrow \frac{1}{{31}} + \frac{1}{{32}} + ... + \frac{1}{{44}} + \frac{1}{{45}} > \frac{1}{{45}} + \frac{1}{{45}} + \frac{1}{{45}} + ... + \frac{1}{{45}} = \frac{{15}}{{45}} = \frac{1}{3}$ $\Rightarrow \frac{1}{{31}} + \frac{1}{{32}} + ... + \frac{1}{{44}} + \frac{1}{{45}} > \frac{1}{{45}} + \frac{1}{{45}} + \frac{1}{{45}} + ... + \frac{1}{{45}} = \frac{{15}}{{45}} = \frac{1}{3}$(1)

Nhận thấy $\frac{1}{{46}} > \frac{1}{{60}};\frac{1}{{47}} > \frac{1}{{60}};...;\frac{1}{{59}} > \frac{1}{{60}}$ $\frac{1}{{46}} > \frac{1}{{60}};\frac{1}{{47}} > \frac{1}{{60}};...;\frac{1}{{59}} > \frac{1}{{60}}$ và từ 46 đến 60 có 15 số

$\Rightarrow \frac{1}{{46}} + \frac{1}{{47}} + ... + \frac{1}{{59}} + \frac{1}{{60}} > \frac{1}{{60}} + \frac{1}{{60}} + \frac{1}{{60}} + ... + \frac{1}{{60}} = \frac{{15}}{{60}} = \frac{1}{4}$ $\Rightarrow \frac{1}{{46}} + \frac{1}{{47}} + ... + \frac{1}{{59}} + \frac{1}{{60}} > \frac{1}{{60}} + \frac{1}{{60}} + \frac{1}{{60}} + ... + \frac{1}{{60}} = \frac{{15}}{{60}} = \frac{1}{4}$(2)

Từ (1) và (2) suy ra

$A = \left( {\frac{1}{{31}} + \frac{1}{{32}} + ... + \frac{1}{{44}} + \frac{1}{{45}}} \right) + \left( {\frac{1}{{46}} + \frac{1}{{47}} + ... + \frac{1}{{60}}} \right) > \frac{1}{3} + \frac{1}{4} = \frac{7}{{12}}$ $A = \left( {\frac{1}{{31}} + \frac{1}{{32}} + ... + \frac{1}{{44}} + \frac{1}{{45}}} \right) + \left( {\frac{1}{{46}} + \frac{1}{{47}} + ... + \frac{1}{{60}}} \right) > \frac{1}{3} + \frac{1}{4} = \frac{7}{{12}}$

-------

Ngoài Đề ôn tập giữa học kì 2 lớp 6 trên, các bạn luyện giải bài tập SGK Ngữ Văn 6 hay SGK môn Toán lớp 6 được VnDoc sưu tầm, chọn lọc. Đồng thời các dạng đề thi học kì 1 lớp 6, đề thi học kì 2 lớp 6 mới nhất được cập nhật. Mời các em học sinh, các thầy cô cùng các bậc phụ huynh tham khảo đề thi, bài tập mới nhất.

Chia sẻ, đánh giá bài viết

24

2.325

Bài trước

Bài sau