Bài tập Khi nào thì xOy + yOz = xOz? nâng cao
Bài tập nâng cao Toán lớp 6: Khi nào thì xOy + yOz = xOz?
Bài tập nâng cao Toán lớp 6: Khi nào thì xOy + yOz = xOz do VnDoc biên soạn bao gồm 2 phần Trắc nghiệm và Tự luận có đáp án chi tiết cho từng phần giúp các em học sinh ôn tập, củng cố kỹ năng giải Toán lớp 6 Chương 2 Hình học, chuẩn bị cho các bài thi môn Toán lớp 6 trong năm học. Mời các em học sinh tham khảo chi tiết.
Lý thuyết và Bài tập Khi nào thì xOy + yOz = xOz lớp 6:
- Giải bài tập SBT Toán 6 bài 4: Khi nào thì xOy + yOz = xOz
- Giải bài tập SGK Toán lớp 6 - Hình học Chương 2: xOy + yOz = xOz
- Lý thuyết Toán lớp 6: Khi nào thì xOy + yOz = xOz
Bài tập nâng cao Toán lớp 6: Khi nào thì xOy + yOz = xOz?
A. Lý thuyết cần nhớ về điều kiện để xOy + yOz = xOz
1. Tính chất cộng số đo hai góc
+ Nếu tia Oy nằm giữa tia Ox và tia Oz thì 
\(\widehat {xOy} + \widehat {yOz} = \widehat {xOz}\)
+ Ngược lại nếu \(\widehat {xOy} + \widehat {yOz} = \widehat {xOz}\) thì tia Oy nằm giữa hai tia Ox và Oz
+ Lưu ý: Nếu tia Oy nằm giữa hai tia Ox và Ot; tia Oz nằm giữa hai tia Oy và Ot thì \(\widehat {xOy} + \widehat {yOz} + \widehat {zOt} = \widehat {xOt}\)
2. Hai góc kề nhau, phụ nhau, bù nhau
+ Hai góc kề nhau là hai góc có một cạnh chung và hai cạnh còn lại nằm trên hai nửa mặt phẳng đối nhau có bờ chứa cạnh chung
+ Hai góc phụ nhau là hai góc có tổng số đo bằng 90º
+ Hai góc bù nhau là hai góc có tổng số đo bằng 180º
+ Hai góc kề bù là hai góc vừa kề nhau vừa bù nhau
+ Hai góc cùng phụ (hoặc cùng bù) với một góc thứ ba thì bằng nhau
B. Bài tập vận dụng về khi nào thì xOy + yOz = xOz
I. Bài tập trắc nghiệm
Câu 1: Chọn phát biểu đúng trong các phát biểu sau:
A. Với Ox, Oy, Oz là ba tia chung gốc thì \(\widehat {xOy} + \widehat {yOz} = \widehat {xOz}\)
B. Hai góc tù là hai góc kề nhau
C. Nếu \(\widehat A;\widehat B\)là hai góc bù nhau thì \(\widehat A + \widehat B = {90^0}\)
D. Nếu tia Op nằm giữa hai tia Om và On thì ta có \(\widehat {mOp} + \widehat {pOn} = \widehat {mOn}\)
Câu 2: Cho góc \(\widehat {xOm}\) và \(\widehat {mOn}\) là hai góc phụ nhau. Nếu \(\widehat {xOm} = {45^0}\)thì góc \(\widehat {mOn}\) có số đo bằng:
A. 53º B. 65º C. 45º D. 35º
Câu 3: Cho ba tia chung gốc OA, OB, OC với \(\widehat {AOB} = {100^0};\widehat {BOC} = {40^0};\widehat {AOC} = {140^0}\). Chọn phát biểu đúng trong các phát biểu sau:
A. Tia OB nằm giữa hai tia OA và OC
B. Tia OA nằm giữa hai tia OB và OC
C. Tia OC nằm giữa hai tia OA và OB
D. Ba điểm A, B, C thẳng hàng
Câu 4: Cho \(\widehat A;\widehat B\) là hai góc phụ nhau và \(\widehat A - \widehat B = {14^0}\). Số đo góc \(\widehat B\) là:
A. 38º B.52º C. 16º D. 54º
Câu 5: Cho hình vẽ dưới đây. Số đo của góc là:
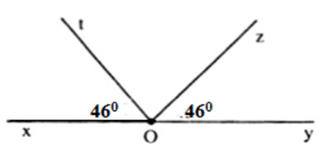
A. 98º B. 88º C. 78º D.108º
II. Bài tập tự luận
Bài 1: Chứng tỏ rằng nếu hai tia Ox, Oy thuộc hai nửa mặt phẳng đối nhau bờ chứa tia Oz và thì Ox và Oy là hai tia đối nhau
Bài 2: Cho điểm B nằm giữa hai điểm A và C, điểm D nằm giữa hai điểm B và C, điểm O nằm ngoài đường thẳng AC, biết rằng \(\widehat {AOD} = {80^0};\widehat {BOD} = {40^0}\). Tính \(\widehat {AOB}\)
Bài 3: Cho góc vuông AOB, tia OC nằm giữa hai tia OA và OB, biết \(\widehat {AOC} - 2.\widehat {COB} = {30^0}\). Tính số đo các góc \(\widehat {AOC};\widehat {BOC}\)
Bài 4: Gọi O là giao điểm của ba đường thẳng xy, uv, zt. Tính số đo góc tOv, biết rằng \(\widehat {xOz} = {65^0};\widehat {vOy} = {35^0}\)
C. Lời giải bài tập về khi nào thì xOy + yOz = xOz
I. Bài tập trắc nghiệm
| Câu 1 | Câu 2 | Câu 3 | Câu 4 | Câu 5 |
| D | C | A | A | B |
II. Bài tập tự luận
Bài 1:
Gọi Oy’ là tia đối của tia Ox suy ra hai tia Ox và Oy’ thuộc hai nửa mặt phẳng đối nhau có bờ chứa tia Oz. Do đó hai tia Oy và Oy’ cùng thuộc một nửa mặt phẳng có bờ chứa tia Oz
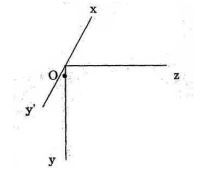
a, Ta có \(\widehat {zOx} + \widehat {zOy'} = {180^0}\)(kề bù)
Nên \(\widehat {zOy'} = {180^0} - \widehat {zOx}\)
Mà \(\widehat {zOy} = {180^0} - \widehat {zOx}\)(vì \(\widehat {zOx} + \widehat {zOy} = {180^0}\))
Suy ra
Trên cùng một nửa mặt phẳng bời chứa tia Oz, có hai tia Oy và Oy’ mà \(\widehat {zOy} = \widehat {zOy'}\)nên hai tia Oy và Oy’ phải trùng nhau
Do vậy hai tia Ox và Oy là hai tia đối nhau
Bài 2:
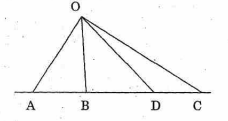
Vì điểm B nằm giữa A và C, điểm D nằm giữa B và C nên điểm B nằm giữa A và D. Ta có tia OB nằm giữa hai tia OA và OD. Do đó:
\(\begin{array}{l}
\widehat {AOB} + \widehat {BOD} = \widehat {AOD}\\
\widehat {AOB} + {40^0} = {80^0}\\
\widehat {AOB} = {80^0} - {40^0} = {40^0}
\end{array}\)
Bài 3:
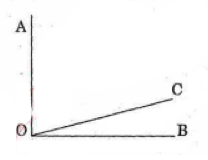
Ta có \(\widehat {AOB} = {90^0}\), tia Oc nằm giữa hai tia OA, OB nên
\(\begin{array}{l}
\widehat {AOC} + \widehat {COB} = {90^0}\\
\widehat {AOC} = {90^0} - \widehat {COB}
\end{array}\)
Lại có \(\widehat {AOC} - 2.\widehat {COB} = {30^0}\)
Suy ra \(90^0-\widehat{COB} -2.\widehat{COB} = 30^0\)
\(\begin{array}{l}
{90^0} - 3.\widehat {COB} = {30^0}\\
3.\widehat {COB} = {90^0} - {30^0} = {60^0}\\
\Rightarrow \widehat {COB} = {20^0}\\
\Rightarrow \widehat {AOC} = {90^0} - {20^0} = {70^0}
\end{array}\)
Bài 4:
TH1: Nếu hai tia Ov và Oz nằm trên hai nửa mặt phẳng đối nhau bờ xy
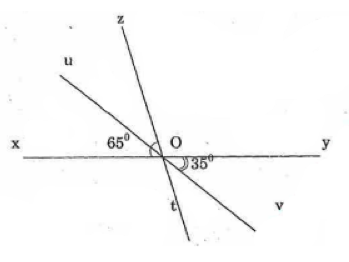
Ta có
\(\begin{array}{l}
\widehat {xOz} + \widehat {zOy} = {180^0}\\
\widehat {tOy} + \widehat {zOy} = {180^0}\\
\Rightarrow \widehat {tOy} = \widehat {xOz} = {65^0}
\end{array}\)
Tia Ov nằm giữa hai tia Ot và Oy (do \(\widehat {yOv} < \widehat {yOt}\)) nên:
\(\begin{array}{l}
\widehat {tOv} + \widehat {vOy} = \widehat {tOy}\\
\widehat {tOv} + {35^0} = {65^0}\\
\widehat {tOv} = {65^0} - {35^0} = {30^0}
\end{array}\)
TH2: Nếu hai tia Ox và Oz cùng nằm trong một nửa mặt phẳng bờ xy, ta có \(\widehat {zOx} + \widehat {yOz} = {180^0};\widehat {tOy} + \widehat {yOz} = {180^0}\)
Suy ra \(\widehat {tOy} = \widehat {zOx} = {65^0}\)
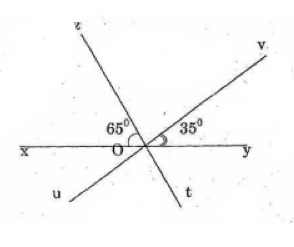
Vì tia Oy nằm giữa hai tia Ov và Ot nên \(\widehat {tOv} = \widehat {tOy} + \widehat {yOv} = {65^0} + {35^0} = {100^0}\)
---------
Trên đây VnDoc tổng hợp các kiến thức Bài tập Toán lớp 6: Khi nào thì xOy + yOz = xOz, ngoài ra các em học sinh có thể tham khảo các bài giải SGK môn Toán lớp 6, Môn Ngữ văn 6, Môn Vật lý 6, môn Sinh Học 6, Lịch sử 6, Địa lý 6....và các đề thi học kì 1 lớp 6 và đề thi học kì 2 lớp 6 để chuẩn bị cho các bài thi đề thi học kì đạt kết quả cao.
