Giải bài tập SBT Toán 6 bài 4: Khi nào thì xOy + yOz = xOz

Bài tập môn Toán lớp 6

Giải bài tập SBT Toán hình 6 bài 4: Khi nào thì xOy + yOz = xOz được VnDoc sưu tầm và đăng tải, tổng hợp lý thuyết. Đây là lời giải hay cho các câu hỏi trong sách bài tập nằm trong chương trình giảng dạy môn Toán lớp 6. Hi vọng rằng đây sẽ là những tài liệu hữu ích trong công tác giảng dạy và học tập của quý thầy cô và các em học sinh.

Giải bài tập SBT Toán Hình 6 bài 2: Góc

Giải bài tập SBT Toán 6 bài 3: Số đo góc

Giải bài tập SBT Toán hình 6 bài 1: Nửa mặt phẳng

Câu 1: Gọi Oz là tia nằm giữa hai tia Ox, Oy.

Biết ∠(xOy) = a^o, ∠(zOx) = b^o. Tính (yOz)

Lời giải:

Vì tia Oz nằm giữa hai tia Ox, Oy nên:

∠(xOy) = ∠(yOz) + ∠(xOz) ⇒ ∠(yOz) = ∠(xOy) - ∠(xOz) = a^o – b^o

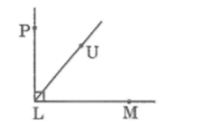
Câu 2: Cho biết ∠(LPM) = 90^o. Vẽ tia PU để ∠(LPM) = ∠(LPU) + ∠(UPM)

Lời giải:

Lấy điểm U nằm trong góc LPM, Vẽ tia PU. Vì tia PU nằm giữa hai tia PL và PM nên: ∠(LPM) = ∠(LPU) + ∠(UPM)

Như hình vẽ bên:

Câu 3: Ở hình dưới, hai tia OI , OK đối nhau. Tia OI cắt đoạn thẳng AB tại I. Biết ∠(KOA) = 120^o, ∠(BOI) = 45^o

Tính ∠(KOB), ∠(AOI), ∠(BOA)

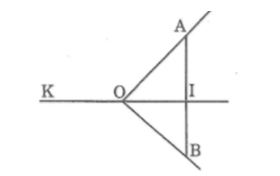
Lời giải:

Vì ∠(KOB) và ∠(BOI) kề bù nên ∠(KOB) + ∠(BOI) = 180^o

Suy ra: ∠(KOB) = 180o - ∠(BOI) = 180^o – 45o = 135^o

Vì ∠(KOA) và ∠(AOI) kề bù nên ∠(KOA) + ∠(AOI) = 180^o

Suy ra: ∠(AOI) = 180 - ∠(KOA) = 180^o – 120^o = 60^o

Vì tia OI nằm giữa hai tia OA và OB nề:

∠(AOI) + ∠(BOI) = ∠(AOB)

Suy ra : ∠(AOB) = 60^o + 45^o = 105^o

Câu 4: Xem hình dưới, làm thế nào để chỉ đo hai góc mà biết được số đo của cả ba góc xOy, xOz, yOz

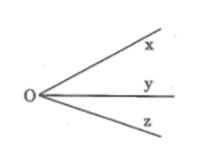
Lời giải:

Trong hình vẽ, tia Oy nằm giữa hai tia Ox và Oz nên:

∠(xOz) = ∠(xOy) + ∠(yOz)

Do vậy, ta chỉ cần đo hai góc (xOy) và (yOz) rồi suy ra góc (xOz) hoặc đo hai góc (xOy) và (xOz) rồi suy ra góc (yOz)

Câu 5: Xem hình dưới. Hỏi ∠(tOv) có phải là góc vuông hay không? Vì sao?

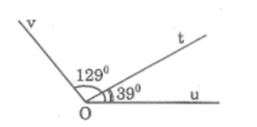
Lời giải:

Vì tia Ot nằm giữa hai tia Ou và Ov nên:

∠(uOt) = ∠(tOv) + ∠(uOv)

Suy ra: ∠(tOv) = ∠(uOv) - ∠(uOt) = 129^o – 39^o = 90^o

Vậy ∠(tOv) là góc vuông

Câu 6: Tia Oy nằm giữa hai tia Ox và Oz. Biết ∠(xOy) = 40^o. Hỏi góc xOz là nhọn, vuông, tù hay bẹt nếu số đo của góc yOz lần lượt bằng 30^o, 50^o, 70^o, 140^o

Lời giải:

Vì tia Oy nằm giữa hai tia Ox và Oz nên:

∠(xOz) = ∠(xOy) + ∠(yOz)

Ta có: ∠(xOy) = 40^o, nếu số đo của ∠(yOz) lần lượt bằng 30^o, 50^o, 70^o, 140^o

Thì:

∠(yOz) = 30^o; ∠(xOz) = 40^o + 30^o = 70^o; ∠(xOz) là góc nhọn

∠(yOz) = 50^o; ∠(xOz) = 40^o + 50^o = 90^o; ∠(xOz) là góc vuông

∠(yOz) = 70^o; ∠(xOz) = 40^o + 70^o = 110^o; ∠(xOz) là góc tù

∠(yOz) = 140^o; ∠(xOz) = 40^o + 140^o = 180^o; ∠(xOz) là góc bẹt

Câu 7: Trên đường thẳng d từ trái sang phải ta lấy các điểm A, D, C, B và lấy điểm O nằm ngoài đường thẳng d.

Biết: ∠(AOD) = 30^o , ∠(DOC) = 40^o; ∠(AOB) = 90^o. Tính ∠(AOC), ∠(COB), ∠(DOB)

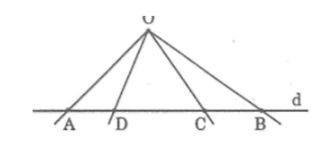
Lời giải:

Vì D nằm giữa A và C nên tia OD nằm giữa hai tia OA và OC.

Suy ra: ∠(AOC) = ∠(AOD) + ∠(DOC) = 30^o + 40^o = 70^o

Vì C nằm giữa A và B nên tia OB nằm giữa hai tia OA và OB.

Suy ra: ∠(AOB) = ∠(AOC) + ∠(COB)

⇒∠(COB) = ∠(AOB) - ∠(AOC) = 90^o - 70^o = 20^o

Vì D nằm giữa A và B nên tia OD nằm giữa hai tia OA và OB.

Suy ra: ∠(AOB) = ∠(AOD) + ∠(DOB)

⇒∠(DOB) = ∠(AOB) - ∠(AOD) = 90^o - 30^o = 60^o