Giải bài tập SBT Toán 6 bài 6: Tia phân giác của góc

Bài tập môn Toán lớp 6

Giải bài tập SBT Toán hình 6 bài 6: Tia phân giác của góc được VnDoc sưu tầm và đăng tải, tổng hợp lý thuyết. Đây là lời giải hay cho các câu hỏi trong sách bài tập nằm trong chương trình giảng dạy môn Toán lớp 6. Hi vọng rằng đây sẽ là những tài liệu hữu ích trong công tác giảng dạy và học tập của quý thầy cô và các em học sinh.

Giải bài tập SBT Toán 6 bài 4: Khi nào thì xOy + yOz = xOz

Giải bài tập SBT Toán 6 bài 5: Vẽ góc cho biết số đo

Giải bài tập SBT Toán 6 bài 7: Thực hành đo góc trên mặt đất

Câu 1: a) Vẽ góc (xOy) = 440

b) Vẽ tia phân giác Oz của góc ấy

Hướng dẫn: Cách 1: Dùng thước đo góc

Cách 2: Gấp giấy

Lời giải:

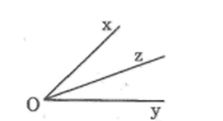
Thực hiện theo hướng dẫn ta có hình vẽ bên

Câu 2: a) Vẽ góc bẹt xOy.

b) Vẽ tia Ot sao cho ∠(xOt) = 30^o

c) Vẽ tia Oz sao cho ∠(yOz) =30^o (Ot và Oz cùng nằm trên một nửa mặt phẳng bờ xy)

d) Vẽ tia phân giác Om của góc tOz;

e) Vì sao tia Om cũng là tia phân giác của xOy?

Lời giải:

a, b, c, d Hình vẽ:

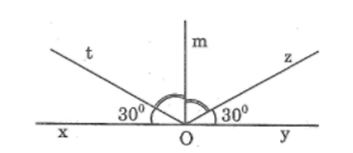
e) Vì ∠(xOt) và ∠(tOy) kề bù nên: ∠(xOt) +∠(tOy) = 180^o

suy ra: ∠(tOy) = 180^o - ∠(xOt) = 180^o – 30^o = 150^o

vì tia Oz nằm giữa Oy và Ot nên ∠(yOt) = ∠(yOz) + ∠(zOt)

suy ra: ∠(zOt) = ∠(yOt) - ∠(yOz) = 150^o – 30^o = 120^o

vì Om là tia phân giác của ∠(tOy) nên:

∠(tOm) = ∠(mOz) = ∠(tOz) /2 = 120/2 = 60^o

Vì tia Ot nằm giữa Ox và Om nên:

∠(xOm) = ∠(xOt) + ∠(tOm) = 30^o + 60^o = 90^o

Vì ∠(xOm) = 90o nên ∠(yOm) = 180^o – 90^o = 90^o

Do ∠(xOm) = ∠(yOm) = 90^o nên Om là tia phân giác của ∠(xOy)

Câu 3: a) Cắt hai góc vuông rồi đặt lên nhau như hình dưới

b) Vì sao có ∠(xOz) = ∠(yOt)

c) Vì sao tia phân giác của yOz cũng là tia phân giác của góc xOt?

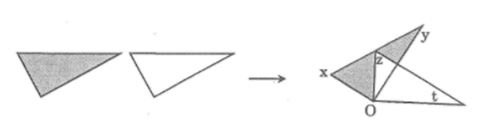
Lời giải:

a) Hình vẽ như hình trên

b) Theo đề bài: ∠(xOy) = ∠(zOt) = 90^o

ta có: ∠(xOz) = ∠(xOy) - ∠(zOy) = 90^o - ∠(tOy) (1)

∠(yOt) = ∠(zOt) - ∠(zOy) = 900 - ∠(tOy) (2)

Từ (1), (2) suy ra: (xOz) = (yOt)

c) Gọi Om là tia phân giác của ∠(zOy), ta có: ∠(zOm) = ∠(mOy)

vì ∠(xOz) = ∠(yOt) nên (xOz) + ∠(zOm) = (yOt) + ∠(mOy)

hay ∠(xOm) = ∠(yOt)

Vậy Om là tia phân giác của (tOy)

Câu 4: Cho hai tia Oy, Oz cùng nằm trong nửa mặt phẳng có bờ chứa tia Ox sao cho ∠(xOy) = 80^o, ∠(xOz) = 30^o. Gọi Om là tia phân giác của góc yOz. Tính ∠(xOm)

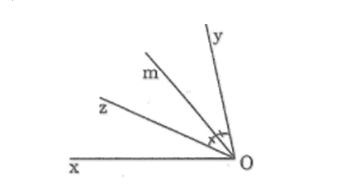
Lời giải:

Vì Oy và Oz cùng nằm trên một nửa mặt phẳng bờ chứa tia Ox, và ∠(xOy) > ∠(xOz)

nên tia Oz nằm giữa hai tia Ox; Oy

suy ra: ∠(xOy) = ∠(xOz) + ∠(zOy)

⇒∠(zOy) = ∠(xOy) - ∠(xOz) = 80^o – 30^o = 50^o

Vì Om là tia phân giác của (yOz) nên:

∠(zOm) = ∠(mOy) = ∠(yOz) /2 = 50/2 = 25^o

Vì Oz nằm giữa Ox và Om: nên ∠(xOm) = ∠(xOz) + ∠(zOm)

Suy ra: ∠(xOm) = 30^o + 25^o = 55^o

Câu 5: Trong trò chơi bi-a, các đấu thủ thường áp dụng kinh nghiệm sau: Muốn đẩy quả cầu A vào điểm O (trên cạnh bàn) để khi bắn ra trúng quả cầu B (Hình bên trái) thì cần xác định điểm O sao cho tia Ot (tia vuông góc với mặt bàn tại O) phải là tia phân giác của góc AOB.

Em hãy xem hình bên phải rồi dùng các dụng cụ đo (thước thẳng, êke, thước đo góc) kiểm tra xem quả cầu C sau khi đập vào cạnh bàn có đập trúng vào quả cầu D không?

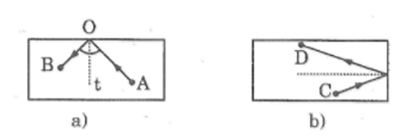
Lời giải:

Thực hành theo hướng dẫn, ta thấy quả cầu C sau khi đập vào cạnh bàn sẽ đập trúng vào quả cầu D