Bài tập Vẽ góc cho biết số đo nâng cao

Bài tập Toán lớp 6 nâng cao

Bài tập Vẽ góc cho biết số đo nâng cao

A. Lý thuyết cần nhớ về cách vẽ góc khi biết số đo
B. Bài tập vận dụng về vẽ góc khi biết số đo
C. Lời giải bài tập về vẽ góc khi biết số đo

Bài tập nâng cao Toán lớp 6: Vẽ góc cho biết số đo do VnDoc sưu tầm bao gồm các bài tập Tự luận có đáp án chi tiết cho từng phần giúp các em học sinh ôn tập, củng cố kỹ năng giải Toán lớp 6 Chương 2 Hình học, chuẩn bị cho các bài thi môn Toán lớp 6 trong năm học. Mời các em học sinh tham khảo chi tiết.

Lý thuyết và Bài tập Vẽ góc cho biết số đo lớp 6:

Bài tập nâng cao Toán lớp 6: Vẽ góc cho biết số đo

A. Lý thuyết cần nhớ về cách vẽ góc khi biết số đo

1. Cách vẽ góc khi biết số đo

+ Cho tia Ox, vẽ góc xOy sao cho $\widehat {xOy} = {m^0}\left( {0 < m < 180} \right)$ $\widehat {xOy} = {m^0}\left( {0 < m < 180} \right)$. Cách vẽ như sau:

- Đặt thước đo góc sao cho tâm thước trùng với gốc O của tia Ox và tia Ox đi qua vạch 0º

- Kẻ tia Oy qua vạch mº của thước đo góc

2. Dấu hiệu nhận biết tia nằm giữa hai tia

+ Trên cùng nửa mặt phẳng bờ chứa tia Ox có hai tia Oy, Oz sao cho $\widehat {xOy} < \widehat {xOz}$ $\widehat {xOy} < \widehat {xOz}$ thì tia Oy nằm giữa hai tia Oz và Ox

B. Bài tập vận dụng về vẽ góc khi biết số đo

Bài 1: Trên cùng một nửa mặt phẳng bờ chứa tia Ox, xác định hai tia Oy và Oz sao cho $\widehat {xOy} = {135^0};\widehat {xOz} = {45^0}$ $\widehat {xOy} = {135^0};\widehat {xOz} = {45^0}$. Chứng tỏ rằng $\widehat {yOz} = {90^0}$ $\widehat {yOz} = {90^0}$

Bài 2: Cho ba tia Ox, Oy, Oz biết $\widehat {xOy} = {60^0}$ $\widehat {xOy} = {60^0}$và $\widehat {xOz} = {30^0}$ $\widehat {xOz} = {30^0}$. Tính số đo góc yOz

Bài 3: Trên mặt phẳng cho tia Ox. Có thể xác định được bao nhiêu tia Oy sao cho $\widehat {xOy} = {60^0}$ $\widehat {xOy} = {60^0}$

Bài 4: Cho 5 điểm A, B, C, D, E theo thứ tự đó trên đường thẳng a và điểm O nằm ngoài đường thẳng a sao cho: $4\widehat {AOB} = 3\widehat {BOC};5\widehat {COD} = 4\widehat {BOC}$ $4\widehat {AOB} = 3\widehat {BOC};5\widehat {COD} = 4\widehat {BOC}$; $6\widehat {DOE} = 5\widehat {BOC}$ $6\widehat {DOE} = 5\widehat {BOC}$và $\widehat {DOE} - \widehat {AOB} = {5^0}$ $\widehat {DOE} - \widehat {AOB} = {5^0}$. Tính số đo các góc $\widehat {AOB};\widehat {BOC};\widehat {COD};\widehat {DOE}$ $\widehat {AOB};\widehat {BOC};\widehat {COD};\widehat {DOE}$

C. Lời giải bài tập về vẽ góc khi biết số đo

Bài 1:

Học sinh tự vẽ hình

Trên cùng một nửa mặt phẳng bờ chứa tia Ox vì $\widehat {xOy} > \widehat {xOz}\left( {{{135}^0} > {{45}^0}} \right)$ $\widehat {xOy} > \widehat {xOz}\left( {{{135}^0} > {{45}^0}} \right)$nên tia Oz nằm giữa hai tia Ox và Oy

Ta có

$\begin{array}{l} \widehat {xOz} + \widehat {zOy} = \widehat {xOy}\\ {45^0} + \widehat {zOy} = {135^0}\\ \widehat {zOy} = {135^0} - {45^0} = {90^0} \end{array}$ $\begin{array}{l} \widehat {xOz} + \widehat {zOy} = \widehat {xOy}\\ {45^0} + \widehat {zOy} = {135^0}\\ \widehat {zOy} = {135^0} - {45^0} = {90^0} \end{array}$

Bài 2:

Bài toán có hai trường hợp

TH1: Tia Oz nằm giữa hai tia Ox và Oy (học sinh tự vẽ hình)

Ta có

$\begin{array}{l} \widehat {xOz} + \widehat {yOz} = \widehat {xOy}\\ {30^0} + \widehat {yOz} = {60^0}\\ \widehat {yOz} = {60^0} - {30^0} = {30^0} \end{array}$ $\begin{array}{l} \widehat {xOz} + \widehat {yOz} = \widehat {xOy}\\ {30^0} + \widehat {yOz} = {60^0}\\ \widehat {yOz} = {60^0} - {30^0} = {30^0} \end{array}$

TH2: Tia Ox nằm giữa hai tia Oy và Oz (học sinh tự vẽ hình)

Ta có

$\begin{array}{l} \widehat {xOy} + \widehat {xOz} = \widehat {yOz}\\ {60^0} + {30^0} = {90^0} = \widehat {yOz} \end{array}$ $\begin{array}{l} \widehat {xOy} + \widehat {xOz} = \widehat {yOz}\\ {60^0} + {30^0} = {90^0} = \widehat {yOz} \end{array}$

Bài 3:

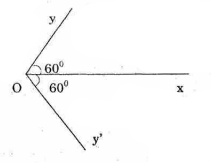
bài tập nâng cao toán lớp 6 vẽ góc cho biết số đo ảnh số 1

Đường thẳng chứa tia Ox chia mặt phẳng thành hai nửa mặt phẳng đối nhau bờ chứa tia Ox. Trên mỗi nửa mặt phẳng có một và chỉ một tia Oy sao cho $\widehat {xOy} = {60^0}$ $\widehat {xOy} = {60^0}$

Vậy trên mặt phẳng chứa tia Ox có hai tia Oy và Oy’ sao cho $\widehat {xOy} = {60^0};\widehat {xOy$ $\widehat {xOy} = {60^0};\widehat {xOy'} = {60^0}$

Bài 4:

Vì $\widehat {DOE} - \widehat {AOB} = {5^0}$ $\widehat {DOE} - \widehat {AOB} = {5^0}$

Nên $12\left( {\widehat {DOE} - \widehat {AOB}} \right) = {60^0}$ $12\left( {\widehat {DOE} - \widehat {AOB}} \right) = {60^0}$

Hay $12\widehat {DOE} - 12\widehat {AOB} = {60^0}$ $12\widehat {DOE} - 12\widehat {AOB} = {60^0}$

Vì $4\widehat {AOB} = 3\widehat {BOC}$ $4\widehat {AOB} = 3\widehat {BOC}$nên $12\widehat {AOB} = 9\widehat {BOC}$ $12\widehat {AOB} = 9\widehat {BOC}$

$6\widehat {DOE} = 5\widehat {BOC}$ $6\widehat {DOE} = 5\widehat {BOC}$ nên $12\widehat {DOE} = 10\widehat {BOC}$ $12\widehat {DOE} = 10\widehat {BOC}$

$\begin{array}{l} \Rightarrow 12\widehat {DOE} - 12\widehat {AOB} = 10\widehat {BOC} - 9\widehat {BOC}\\ 12\widehat {DOE} - 12\widehat {AOB} = \widehat {BOC} \end{array}$ $\begin{array}{l} \Rightarrow 12\widehat {DOE} - 12\widehat {AOB} = 10\widehat {BOC} - 9\widehat {BOC}\\ 12\widehat {DOE} - 12\widehat {AOB} = \widehat {BOC} \end{array}$

Vậy $\widehat {BOC} = {60^0}$ $\widehat {BOC} = {60^0}$

Do đó:

$\begin{array}{l} \widehat {AOB} = {3.60^0}:4 = {45^0}\\ \widehat {COD} = {4.60^0}:5 = {48^0}\\ \widehat {DOE} = {5^0} + {45^0} = {50^0} \end{array}$ $\begin{array}{l} \widehat {AOB} = {3.60^0}:4 = {45^0}\\ \widehat {COD} = {4.60^0}:5 = {48^0}\\ \widehat {DOE} = {5^0} + {45^0} = {50^0} \end{array}$

---------

Trên đây VnDoc tổng hợp các kiến thức Bài tập Toán lớp 6: Vẽ góc cho biết số đo, ngoài ra các em học sinh có thể tham khảo các bài giải SGK môn Toán lớp 6, Môn Ngữ văn 6, Môn Vật lý 6, môn Sinh Học 6, Lịch sử 6, Địa lý 6....và các đề thi học kì 1 lớp 6 và đề thi học kì 2 lớp 6 để chuẩn bị cho các bài thi đề thi học kì đạt kết quả cao.

Chia sẻ, đánh giá bài viết

4

753

Bài trước

Bài sau