Bất phương trình tích: Cách giải nhanh và bài tập minh họa đầy đủ
Cách giải bất phương trình tích Toán 10 - Có đáp án
Bạn đang tìm một phương pháp giải bất phương trình tích nhanh và dễ hiểu? Trong chương trình Bất phương trình Toán 10, dạng toán này thường xuất hiện trong các đề kiểm tra, đề thi, đòi hỏi bạn phải nắm chắc quy tắc xét dấu và xác định điều kiện xác định của biểu thức. Bài viết “Bất phương trình tích: Cách giải nhanh và bài tập minh họa đầy đủ” sẽ giúp bạn hệ thống hóa kiến thức, hướng dẫn chi tiết từng bước, đồng thời cung cấp bài tập bất phương trình Toán 10 có đáp án để bạn luyện tập và nâng cao kỹ năng giải toán hiệu quả.
A. Cách giải bất phương trình tích
Xét biểu thức 
\(P(x)\) có dạng tích các đa thức:
Cách 1: Xét dấu \(P(x)\) bằng phương pháp lập bảng xét dấu (độc giả đọc trong Sách giáo khoa Đại số 10).
Cách 2: Xét dấu \(P(x)\) bằng phương pháp khoảng.
- Bước 1: Giải phương trình \(P(x) =
0\) được các nghiệm \(x_{1} < x_{2}
< ... < x_{n}\).
- Bước 2: Đặt các điểm \(x_{1};x_{2};...;x_{n}\) lên trục số. Các điểm này chia trục số thành n + 1 khoảng.
- Bước 3: Xác định dấu của \(P(x)\) trên một trong các khoảng nói trên (dấu của \(P(x)\) trùng với dấu của \(P(x)\) với a là một điểm tùy ý thuộc khoảng đó).
Ở bước 3, ta thường chọn khoảng chứa số 0 (nếu 0 không phải là một trong các điểm \(x_{1};x_{2};...;x_{n}\)) rồi chọn \(a = 0\).
- Bước 4: Suy ra dấu của \(P(x)\) trên các khoảng còn lại theo quy tắc: “qua” nghiệm bội lẻ thì \(P(x)\) đổi dấu, “qua” nghiệm bội chẵn thì \(P(x)\) không đổi dấu.
B. Bài tập giải bất phương trình tích chi tiết
Ví dụ 1: Xét dấu biểu thức \(P(x) = (x -
1)(x - 2)^{2}(x - 3)^{3}\).
Hướng dẫn giải
Ta có:
\(P(x) = 0 \Leftrightarrow (x - 1)(x -
2)^{2}(x - 3)^{3} = 0\)
\(\Leftrightarrow \left\lbrack
\begin{matrix}
x = 1;x = 2 \\
x = 3 \\
\end{matrix} \right.\)
Trong đó \(x = 1\) và \(x = 3\) là các nghiệm bội lẻ, \(x = 2\) là nghiệm bội chẵn.
Ta có \(P(0) = ( - 1).( - 2)^{2}.( - 3)^{3}
> 0\). Từ đó ta có kết quả xét dấu \(P(x)\):
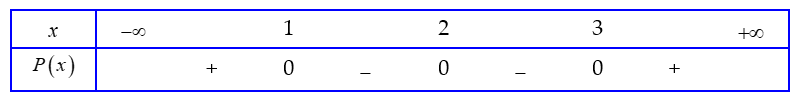
Ví dụ 2: Cho phương trình \((4x - 1)(x + 2)(5 - 3x) \leq 0\). Số nghiệm nguyên trong đoạn [0; 2018] của bất phương trình là:
A. 1 B. 2018 C. 2019 D. 0
Hướng dẫn giải
Ta có:
\((4x - 1)(x + 2)(5 - 3x) = 0\)
\(\Leftrightarrow \left\lbrack
\begin{matrix}
x = \frac{1}{4};x = - 2 \\
x = \frac{5}{3} \\
\end{matrix} \right.\)
Kết quả xét dấu của biểu thức \(P(x) = (4x
- 1)(x + 2)(5 - 3x)\):
Vậy \(P(x) \leq 0 \Leftrightarrow x \in
\left\lbrack - 2;\frac{1}{4} \right\rbrack \cup \left\lbrack
\frac{5}{3}; + \infty \right)\).
Do đó các nghiệm nguyên của bất phương trình \(P(x) \leq 0\) trong đoạn \(\lbrack 0;2018\rbrack\) là 0; 2; 3; …; 2018 có 2018 số.
Với bất phương trình chứa ẩn ở mẫu, không được tùy tiện quy đồng khử mẫu khi chưa xác định được dấu của các biểu thức trong bất phương trình.
-------------------------------------------------
Qua bài viết, bạn đã được trang bị cách giải nhanh bất phương trình tích cùng những bài tập minh họa đầy đủ giúp bạn tự tin xử lý nhiều dạng đề khác nhau. Việc luyện tập đều đặn với những bài tập bất phương trình Toán 10 có đáp án không chỉ giúp bạn rèn kỹ năng xét dấu, tìm nghiệm chính xác mà còn nâng cao tốc độ làm bài trong các kỳ kiểm tra và kỳ thi.
Hãy lưu bài viết này để ôn tập thường xuyên, chia sẻ cho bạn bè để cùng nhau tiến bộ, và đừng quên khám phá thêm các chuyên đề Toán 10 khác như bất phương trình chứa ẩn ở mẫu, bất phương trình chứa tham số hay tam thức bậc hai. Chúc bạn học tốt, giải nhanh – làm đúng mọi bài toán!
