Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm

Đóng

Điểm danh hàng ngày

Hôm nay +3
Ngày 2 +3
Ngày 3 +3
Ngày 4 +3
Ngày 5 +3
Ngày 6 +3
Ngày 7 +5

Bạn đã điểm danh Hôm nay và nhận 3 điểm! Đăng nhập ngay để nhận điểm

Nhắn tin Zalo VNDOC để nhận tư vấn mua gói Thành viên hoặc tải tài liệu Hotline hỗ trợ: 0936 120 169

VnDoc.com

Tìm giá trị lớn nhất, nhỏ nhất của biểu thức F=ax+by trên một miền đa giác

Giải hệ bất phương trình bậc nhất hai ẩn

Bài trước

Tải về

Bài sau

Lớp: Lớp 10

Môn: Toán

Dạng tài liệu: Chuyên đề

Mức độ: Khó

Loại File: Word + PDF

Phân loại: Tài liệu Tính phí

Cách tìm miền nghiệm của hệ bất phương trình bậc nhất hai ẩn

A. Cách giải hệ bất phương trình bậc nhất hai ẩn
B. Bài tập ví dụ minh họa tìm GTLN, GTNN của biểu thức F
C. Bài tập tự rèn luyện có hướng dẫn đáp án

Dạng toán tìm giá trị lớn nhất, nhỏ nhất của biểu thức F trên miền xác định là một đa giác phẳng là nội dung quan trọng trong chương trình Toán lớp 10 (Đại số). Đây là ứng dụng thực tế của việc giải hệ bất phương trình bậc nhất hai ẩn, giúp học sinh rèn luyện kỹ năng tư duy hình học kết hợp đại số. Trong bài viết này, chúng ta sẽ cùng ôn tập cách giải dạng bài này thông qua ví dụ minh họa, phân tích từng bước, kết hợp các kỹ thuật như biểu diễn miền nghiệm, xác định đỉnh đa giác và thay tọa độ vào biểu thức F = ax + by để tìm giá trị lớn nhất và nhỏ nhất. Bài viết phù hợp để ôn tập, luyện thi và củng cố kiến thức nền tảng.

A. Cách giải hệ bất phương trình bậc nhất hai ẩn

Để giải hệ bất phương trình bậc nhất hai ẩn ta thực hiện biểu diễn miền nghiệm của hệ bất phương trình đó:

Bước 1: Trên cùng một mặt phẳng tọa độ, xác định miền nghiệm của mỗi bất phương trình bậc nhất hai ẩn trong hệ:

+ Vẽ đường thẳng d: ax + by = c trên mặt phẳng Oxy

+ Lấy một điểm M₀(x₀; y₀) không thuộc d.

+ Tính ax₀ + by₀ và so sánh với c

+ Nếu ax₀ + by₀ < c thì nửa mặt phẳng bờ d chưa M₀ là miền nghiệm của bất phương trình. Nếu ax₀ + by₀ > c thì nửa mặt phẳng bờ d chứa M₀ là miền nghiệm của bất phương trình.

Bước 2. Gạch bỏ các miền không thỏa mãn.

Bước 3. Kết luận miền không bị gạch là miền nghiệm của hệ bất phương trình đã cho.

B. Bài tập ví dụ minh họa tìm GTLN, GTNN của biểu thức F

Bài tập 1. Tìm giá trị nhỏ nhất của biết thức $F = y - x$ trên miền xác định bởi hệ: $\left\{ \begin{matrix} y - 2x \leq 2 \\ 2y - x \geq 4 \\ x + y \leq 5 \end{matrix} \right.$ $\left\{ \begin{matrix} y - 2x \leq 2 \\ 2y - x \geq 4 \\ x + y \leq 5 \end{matrix} \right.$ ?

Hướng dẫn giải

Ta tìm giao điểm của các cặp đường thẳng trong miền xác định của hệ $\left\{ \begin{matrix} y - 2x \leq 2 \\ 2y - x \geq 4 \\ x + y \leq 5 \end{matrix} \right.$ $\left\{ \begin{matrix} y - 2x \leq 2 \\ 2y - x \geq 4 \\ x + y \leq 5 \end{matrix} \right.$

$\left\{ \begin{matrix} - 2x + y = 2 \\ - x + 2y = 4 \end{matrix} \right.\ \Leftrightarrow \left\{ \begin{matrix} x = 0 \\ y = 2 \end{matrix} \right.\ \Rightarrow A(0;2)$ $\left\{ \begin{matrix} - 2x + y = 2 \\ - x + 2y = 4 \end{matrix} \right.\ \Leftrightarrow \left\{ \begin{matrix} x = 0 \\ y = 2 \end{matrix} \right.\ \Rightarrow A(0;2)$.

$\left\{ \begin{matrix} - 2x + y = 2 \\ x + y = 5 \end{matrix} \right.\ \Leftrightarrow \left\{ \begin{matrix} x = \frac{3}{2} \\ y = \frac{7}{2} \end{matrix} \right.\ \ \Rightarrow B\left( \frac{3}{2};\frac{7}{2} \right)$ $\left\{ \begin{matrix} - 2x + y = 2 \\ x + y = 5 \end{matrix} \right.\ \Leftrightarrow \left\{ \begin{matrix} x = \frac{3}{2} \\ y = \frac{7}{2} \end{matrix} \right.\ \ \Rightarrow B\left( \frac{3}{2};\frac{7}{2} \right)$.

$\left\{ \begin{matrix} x + y = 5 \\ - x + 2y = 4 \end{matrix} \right.\ \Leftrightarrow \left\{ \begin{matrix} x = 2 \\ y = 3 \end{matrix} \right.\ \ \Rightarrow C(2;3)$ $\left\{ \begin{matrix} x + y = 5 \\ - x + 2y = 4 \end{matrix} \right.\ \Leftrightarrow \left\{ \begin{matrix} x = 2 \\ y = 3 \end{matrix} \right.\ \ \Rightarrow C(2;3)$.

Ta tính giá trị của $F = y - x$ tại các giao điểm:

Tại $A(0;2) \Rightarrow F = 2 - 0 = 2$ $A(0;2) \Rightarrow F = 2 - 0 = 2$.

Tại $B\left( \frac{3}{2};\frac{7}{2} \right) \Rightarrow F = \frac{7}{2} - \frac{3}{2} = 2$ $B\left( \frac{3}{2};\frac{7}{2} \right) \Rightarrow F = \frac{7}{2} - \frac{3}{2} = 2$.

Tại $C(2;3) \Rightarrow F = 3 - 2 = 1$ $C(2;3) \Rightarrow F = 3 - 2 = 1$.

Vậy $\min F = 1\ khi\ x = 2,\ \ y = 3$ $\min F = 1\ khi\ x = 2,\ \ y = 3$.

Bài tập 2: Tìm giá trị nhỏ nhất của biết thức $F = x - y$ biết $x;y$ thỏa mãn điều kiện $\left\{ \begin{matrix} 0 \leq y \leq 4 \\ x \geq 0 \\ x - y - 1 \leq 0 \\ x + 2y - 10 \leq 0 \end{matrix} \right.$ $\left\{ \begin{matrix} 0 \leq y \leq 4 \\ x \geq 0 \\ x - y - 1 \leq 0 \\ x + 2y - 10 \leq 0 \end{matrix} \right.$, và biết hệ $\left\{ \begin{matrix} 0 \leq y \leq 4 \\ x \geq 0 \\ x - y - 1 \leq 0 \\ x + 2y - 10 \leq 0 \end{matrix} \right.$ $\left\{ \begin{matrix} 0 \leq y \leq 4 \\ x \geq 0 \\ x - y - 1 \leq 0 \\ x + 2y - 10 \leq 0 \end{matrix} \right.$ có miền nghiệm là phần tô đậm trong hình vẽ bên dưới.

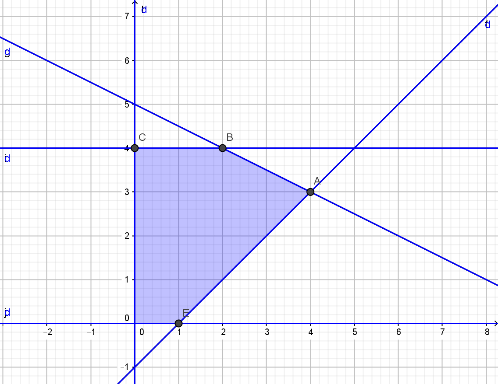
Hướng dẫn giải

Miền nghiệm là ngũ giác $ABCOE$ với $A(4\ ;\ 3),\ B(2\ ;\ 4),\ C(0\ ;\ 4),\ E(1\ ;\ 0),O(0\ ;\ 0)$ $A(4\ ;\ 3),\ B(2\ ;\ 4),\ C(0\ ;\ 4),\ E(1\ ;\ 0),O(0\ ;\ 0)$.

Tại $A(4\ ;\ 3)$ $A(4\ ;\ 3)$ thì $F = 1.$

Tại $B(2\ ;\ 4)$ $B(2\ ;\ 4)$ thì $F = - 2.$

Tại $C(0\ ;\ 4)$ $C(0\ ;\ 4)$thì $F = - 4.$

Tại $E(1;\ 0)$ $E(1;\ 0)$thì $F = 1.$

Tại $O(0\ ;\ 0)$ $O(0\ ;\ 0)$thì $F = 0.$

Vậy $\min F = - 4$ $\min F = - 4$

Bài tập 3: Tìm giá trị nhỏ nhất của biểu thức $F(x;y) = x - y$ với điều kiện $\left\{ \begin{matrix} x \geq 0 \\ y \geq 0 \\ x + y - 3 \leq 0 \end{matrix} \right.$ $\left\{ \begin{matrix} x \geq 0 \\ y \geq 0 \\ x + y - 3 \leq 0 \end{matrix} \right.$.

Hướng dẫn giải

Tìm giá trị nhỏ nhất của biểu thức $F(x;y) = x - y$ với điều kiện $\left\{ \begin{matrix} x \geq 0 \\ y \geq 0 \\ x + y - 3 \leq 0 \end{matrix} \right.$ $\left\{ \begin{matrix} x \geq 0 \\ y \geq 0 \\ x + y - 3 \leq 0 \end{matrix} \right.$.

Vẽ đường thẳng $d_{1}:x = 0$ $d_{1}:x = 0$ đi qua hai điểm $(0;0)$ và$(0;1)$.

Vẽ đường thẳng $d_{2}:y = 0$ $d_{2}:y = 0$ đi qua hai điểm $(0;0)$ và $(1;0)$.

Vẽ đường thẳng $d_{3}:x + y - 3 = 0$ $d_{3}:x + y - 3 = 0$ đi qua hai điểm $(0;3)$ và $(3;0)$.

Xét điểm$M(1;1)$. Ta thấy tọa độ M thỏa mãn tất cả các bất phương trình trong hệ.

Do đó, miền nghiệm của hệ bất phương trình $\left\{ \begin{matrix} x \geq 0 \\ y \geq 0 \\ x + y - 3 \leq 0 \end{matrix} \right.$ $\left\{ \begin{matrix} x \geq 0 \\ y \geq 0 \\ x + y - 3 \leq 0 \end{matrix} \right.$ là miền không bị tô đậm

Tìm tọa độ các điểm O; A; B.

Điểm $O = d_{1} \cap d_{2}$ $O = d_{1} \cap d_{2}$ nên tọa độ điểm O là nghiệm của hệ $\left\{ \begin{matrix} x = 0 \\ y = 0 \end{matrix} \right.$ $\left\{ \begin{matrix} x = 0 \\ y = 0 \end{matrix} \right.$. Vậy O(0; 0).

Điểm $A = d_{1} \cap d_{3}$ $A = d_{1} \cap d_{3}$ nên tọa độ điểm A là

nghiệm của hệ $\left\{ \begin{matrix} x = 0 \\ x + y - 3 = 0 \end{matrix} \right.\ \Leftrightarrow \left\{ \begin{matrix} x = 0 \\ y = 3 \end{matrix} \right.$ $\left\{ \begin{matrix} x = 0 \\ x + y - 3 = 0 \end{matrix} \right.\ \Leftrightarrow \left\{ \begin{matrix} x = 0 \\ y = 3 \end{matrix} \right.$. Vậy $A(0;3)$.

Điểm $B = d_{2} \cap d_{3}$ $B = d_{2} \cap d_{3}$ nên tọa độ điểm B là nghiệm của hệ $\left\{ \begin{matrix} y = 0 \\ x + y - 3 = 0 \end{matrix} \right.\ \Leftrightarrow \left\{ \begin{matrix} x = 3 \\ y = 0 \end{matrix} \right.$ $\left\{ \begin{matrix} y = 0 \\ x + y - 3 = 0 \end{matrix} \right.\ \Leftrightarrow \left\{ \begin{matrix} x = 3 \\ y = 0 \end{matrix} \right.$.

Vậy $B(3;0)$.

Ta thấy $F(x;y) = x - y$ đạt giá trị nhỏ nhất chỉ có thể tại các điểm O; A; B.

Tại O(0; 0). Thì. $F = 0$

Tại $A(0;3)$ thì $F = - 3$

Tại $B(3;0)$ thì $F = 3$

Vậy giá trị nhỏ nhất của biểu thức $F(x;y) = x - y$ trên miền xác định bởi hệ $\left\{ \begin{matrix} x \geq 0 \\ y \geq 0 \\ x + y - 3 \leq 0 \end{matrix} \right.$ $\left\{ \begin{matrix} x \geq 0 \\ y \geq 0 \\ x + y - 3 \leq 0 \end{matrix} \right.$ là -3

Bài tập 4. Cho các giá trị $x,y$ thỏa mãn điều kiện $\left\{ \begin{matrix} x - y + 2 \geq 0 \\ 2x - y - 1 \leq 0 \\ 3x - y - 2 \geq 0 \end{matrix} \right.$ $\left\{ \begin{matrix} x - y + 2 \geq 0 \\ 2x - y - 1 \leq 0 \\ 3x - y - 2 \geq 0 \end{matrix} \right.$. Tìm giá trị lớn nhất của biểu thức $T = 3x + 2y$.

Hướng dẫn giải

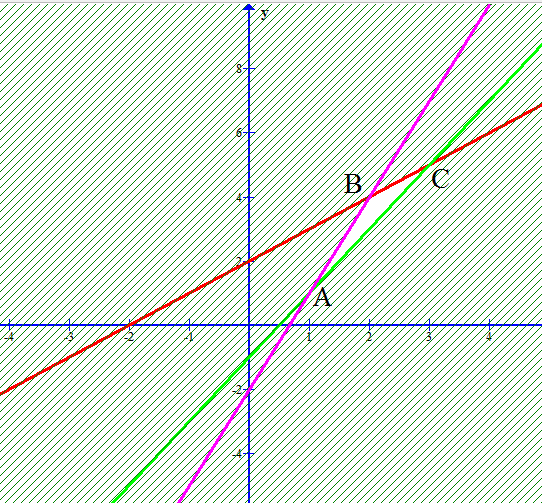
Miền nghiệm của hệ đã cho là miền trong tam giác $ABC$(Kể cả đường biên) trong đó $A(1;1)$, $B(2;4)$,$C(3;5)$.

Giá trị lớn nhất của $T = 3x + 2y$ đạt được tại các đỉnh của tam giác $ABC$.

Do $T_{A} = T(1;1) = 3.1 + 2.1 = 5$ $T_{A} = T(1;1) = 3.1 + 2.1 = 5$, $T_{B} = T(2;4) = 3.2 + 2.4 = 14$ $T_{B} = T(2;4) = 3.2 + 2.4 = 14$ và $T_{C} = T(3;5) = 3.3 + 2.5 = 25$ $T_{C} = T(3;5) = 3.3 + 2.5 = 25$ nên giá trị lớn nhất của $T = 3x + 2y$ là $25$ đạt được khi $x = 3$ và $y = 5$.

C. Bài tập tự rèn luyện có hướng dẫn đáp án

Bài 1. Tìm giá trị nhỏ nhất của biểu thức $F = 3y - 2x$ trên miền xác định bởi hệ $\left\{ \begin{gathered} x - y \leqslant 6 \hfill \\ y - 2x \geqslant 2 \hfill \\ x + y \leqslant 4 \hfill \\ \end{gathered} \right.$ $\left\{ \begin{gathered} x - y \leqslant 6 \hfill \\ y - 2x \geqslant 2 \hfill \\ x + y \leqslant 4 \hfill \\ \end{gathered} \right.$.

Bài 2. Một người dùng ba loại nguyên liệu $A,B,C$ để sản xuất ra hai loại sản phẩm $P$ và $Q$. Để sản xuất $1\ kg$ $1\ kg$ mỗi loại sản phẩm $P$ hoặc $Q$ phải dùng một số kilôgam nguyên liệu khác nhau. Tổng số kilôgam nguyên liệu mỗi loại mà người đó có và số kilôgam từng loại nguyên liệu cần thiết để sản xuất ra 1 kg sản phẩm mỗi loại được cho trong bảng sau:

Biết $1\ kg$ $1\ kg$ sản phẩm $P$ có lợi nhuận 3 triệu đồng và $1\ kg$ $1\ kg$ sản phẩm $Q$ có lợi nhuận 5 triệu đồng. Người đó đã lập được phương án sản xuất hai loại sản phẩm trên sao cho có lãi cao nhất. Hỏi lãi cao nhất bằng bao nhiêu?

Bài 3: Giá trị lớn nhất của biểu thức$F(x;y) = x + 2y$, với điều kiện $\left\{ \begin{matrix} 0 \leq y \leq 4 \\ x \geq 0 \\ x - y - 1 \leq 0 \\ x + 2y - 10 \leq 0 \end{matrix} \right.$ $\left\{ \begin{matrix} 0 \leq y \leq 4 \\ x \geq 0 \\ x - y - 1 \leq 0 \\ x + 2y - 10 \leq 0 \end{matrix} \right.$ là bao nhiêu?

Tài liệu quá dài để hiển thị hết — hãy nhấn Tải về để xem trọn bộ!

------------------------------------------------

FAQ?

1. Cách tìm giá trị lớn nhất, nhỏ nhất của F = a x + b y trên miền đa giác?
Xác định miền nghiệm của hệ bất phương trình, tìm các đỉnh của đa giác rồi tính F = a x + b y tại từng đỉnh. Giá trị lớn nhất và nhỏ nhất trong các kết quả thu được chính là đáp án.

2. Vì sao phải tìm các đỉnh của miền đa giác?
Với hàm mục tiêu dạng F = a x + b y , giá trị lớn nhất hoặc nhỏ nhất trên một miền đa giác thường đạt tại một đỉnh của miền đó.

3. Các bước giải bài toán tối ưu tuyến tính Toán 10 là gì?
Gồm: biểu diễn miền nghiệm của hệ bất phương trình trên mặt phẳng tọa độ, xác định các đỉnh, tính giá trị biểu thức tại từng đỉnh và kết luận giá trị lớn nhất, giá trị nhỏ nhất.

4. Miền đa giác được xác định như thế nào?
Miền đa giác là phần giao của các nửa mặt phẳng nghiệm tương ứng với những bất phương trình bậc nhất hai ẩn trong hệ đã cho.

5. Có cần giải hệ phương trình để tìm các đỉnh không?
Có. Khi hai đường thẳng biên cắt nhau, tọa độ giao điểm được tìm bằng cách giải hệ hai phương trình bậc nhất hai ẩn tương ứng.

6. Giá trị lớn nhất, nhỏ nhất của F = a x + b y có nhất thiết tồn tại không?
Không phải lúc nào cũng có. Nếu miền nghiệm không bị chặn hoặc điều kiện bài toán không đảm bảo, giá trị lớn nhất hoặc giá trị nhỏ nhất có thể không tồn tại.

7. Bài toán tìm GTLN, GTNN trên miền đa giác thuộc chuyên đề nào?
Đây là dạng toán thuộc chuyên đề hệ bất phương trình bậc nhất hai ẩn, thường được sử dụng để rèn luyện kỹ năng biểu diễn miền nghiệm và giải bài toán tối ưu trong Toán 10.

-------------------------------

Hy vọng qua bài viết “Tìm giá trị lớn nhất, nhỏ nhất của biểu thức F = ax + by trên một miền đa giác”, bạn đã nắm vững được phương pháp giải hệ bất phương trình bậc nhất hai ẩn và cách xác định miền nghiệm đa giác để tìm giá trị tối ưu của biểu thức tuyến tính. Đây là kỹ năng quan trọng không chỉ giúp bạn làm tốt các bài toán trong chương trình Toán lớp 10 mà còn là nền tảng cho những bài toán tối ưu phức tạp hơn trong các kỳ thi.

Nếu bạn thấy bài viết hữu ích, đừng quên chia sẻ và theo dõi thêm các bài viết khác về Toán để nâng cao kỹ năng giải toán và ôn luyện hiệu quả. Chúc bạn học tập tốt và thành công trong mọi bài thi!

Tải về

Chọn file muốn tải về: