Tính độ dài vectơ Toán 10
Bài tập tính độ dài vectơ lớp 10
Trong Toán học, đặc biệt là trong chương trình Toán lớp 10, việc tính độ dài vectơ là một khái niệm quan trọng và cần thiết để giải quyết các bài toán hình học không gian, động học và nhiều lĩnh vực khác. Tính độ dài vectơ không chỉ giúp học sinh hiểu rõ hơn về mối quan hệ giữa các điểm trong không gian mà còn là bước đầu tiên để giải quyết các bài toán phức tạp hơn liên quan đến vectơ. Trong bài viết này, chúng ta sẽ tìm hiểu chi tiết về cách tính độ dài vectơ, các công thức liên quan và cách áp dụng chúng vào các bài toán thực tế.
A. Độ dài vectơ
- Độ dài của vectơ là khoảng cách giữa điểm đầu và điểm cuối của vectơ đó.
- Độ dài của vectơ
\(\overrightarrow{AB};\overrightarrow{a}\) tương ứng kí hiệu là \(\left|
\overrightarrow{AB} \right|;\left| \overrightarrow{a}
\right|\).
B. Bài tập ví dụ minh họa tính độ dài vectơ
Bài tập 1: Cho hình chữ nhật \(ABCD\) có \(AB =
4a\) và \(AD = 3a\). Tính độ dài của vecto \(\overrightarrow{BA} +
\overrightarrow{DA}\)?
A. \(5a\). B. \(6a\). C. \(7a\). D. \(2a\sqrt{3}\).
Hướng dẫn giải
Từ \(B\) kẻ \(\overrightarrow{BE} =
\overrightarrow{DA}\)
Áp dụng quy tắc hình hình hành: \(\overrightarrow{BA} + \overrightarrow{DA} =
\overrightarrow{BA} + \overrightarrow{BE} =
\overrightarrow{BF}\)(Với \(F\) là đỉnh thứ tư của hình chữ nhật \(ABEF\)
\(\Rightarrow \left| \overrightarrow{BF}
\right| = \sqrt{(4a)^{2} + (3a)^{2}} = 5a\).
Bài tập 2: Cho tam giác \(ABC\) đều cạnh bằng \(1\). Tính độ dài của vectơ tổng \(\overrightarrow{u} =
\overrightarrow{AB} + \overrightarrow{AC}\)?
Hướng dẫn giải
Hình vẽ minh họa
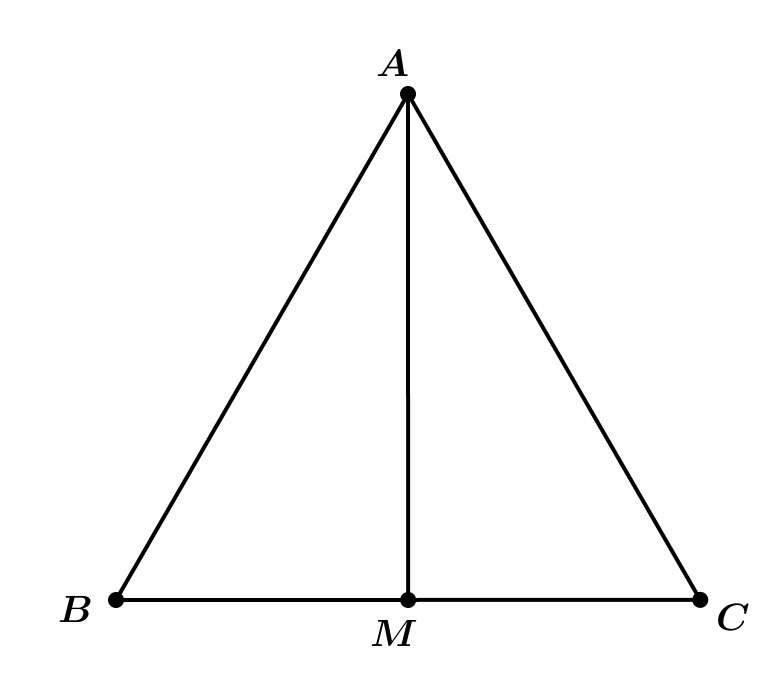
Gọi \(M\) là trung điểm của \(BC\). Tam giác \(ABC\) đều nên \(AM = \frac{\sqrt{3}}{2}\).
Ta có: \(\overrightarrow{u} =
\overrightarrow{AB} + \overrightarrow{AC} =
2\overrightarrow{AM}\)
\(\Rightarrow \left| \overrightarrow{u}
\right| = 2\left| \overrightarrow{AM} \right| = 2.AM =
2.\frac{\sqrt{3}}{2} = \sqrt{3}\)
Bài tập 3: Cho tam giác \(ABC(AB <
AC),AD\) là phân giác trong của góc \(A\). Qua trung điểm \(M\) của cạnh \(BC\), ta kẻ đường thẳng song song với \(AD\), cắt cạnh \(AC\) tại \(E\) và cắt tia \(BA\) tại \(F\). Biết rằng \(AB = 6\) và \(4BD
= 3BM\). Tính: \(|\overrightarrow{CM} -
\overrightarrow{EM}|?\)
Hướng dẫn giải
Hình vẽ minh họa
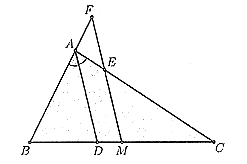
Ta có: \(\overrightarrow{CM} -
\overrightarrow{EM} = \overrightarrow{CM} + \overrightarrow{ME} =
\overrightarrow{CE}\)
Ta có: \(ME//AD \Rightarrow \frac{CE}{CA} =
\frac{CM}{CD}(1)\); \(AD//MF
\Rightarrow \frac{BA}{BF} = \frac{BD}{BM}(2)\)
Nhân theo vế (1), (2) với \(BM =
CM\), ta được: \(\frac{CE}{BF} \cdot
\frac{AB}{AC} = \frac{BD}{CD}\ \ \ (3)\).
Theo giả thiết, \(AD\) là phân giác của góc \(A\) nên \(\frac{BD}{CD} = \frac{AB}{AC}\) (4).
Từ (3) và (4) suy ra \(\frac{CE}{BF} = 1
\Rightarrow CE = BF\) (5).
Từ (2): \(\frac{BA}{BF} = \frac{BD}{BM} =
\frac{3}{4} \Rightarrow BF = \frac{4}{3}BA = \frac{4}{3} \cdot 6 =
8\) (6).
Từ (5) và (6) suy ra \(CE = BF =
8\).
Vậy \(|\overrightarrow{CM} -
\overrightarrow{EM}| = |\overrightarrow{CE}| = CE = 8\).
C. Bài tập tự rèn luyện tính độ dài vectơ có hướng dẫn chi tiết
Bài 1. Cho tam giác \(ABC\) đều cạnh \(a\), \(M\) là trung điểm của \(BC\). Tính \(\left| \overrightarrow{CA} - \overrightarrow{MC}
\right|\)?
A. \(\left| \overrightarrow{CA} -
\overrightarrow{MC} \right| = \frac{2\sqrt{3}a}{3}\). B. \(\left| \overrightarrow{CA} - \overrightarrow{MC}
\right| = \frac{a\sqrt{7}}{2}\).
C. \(\left| \overrightarrow{CA} -
\overrightarrow{MC} \right| = \frac{a}{2}\). D. \(\left| \overrightarrow{CA} - \overrightarrow{MC}
\right| = \frac{3a}{2}\).
Bài 2: Gọi \(G\) là trọng tâm tam giác vuông \(ABC\) với cạnh huyền \(BC = 12\). Vectơ \(\overrightarrow{GB} - \overrightarrow{CG}\) có độ dài bằng bao nhiêu?
A. \(8\). B. \(4\). C. \(2\). D. \(2\sqrt{3}\).
Bài 3: Cho tam giác \(ABC\) vuông cân tại \(A\), cạnh \(AB = a\). Khi đó \(\left| 2\overrightarrow{AB} - \overrightarrow{AC}
\right|\) bằng
A. \(a\sqrt{5}\). B. \(a\sqrt{2}\). C. \(a\sqrt{3}\). D. \(a\).
Bài 4: Cho M là một điểm nằm trên đường tròn ngoại tiếp tam giác \(\Delta ABC\) đều cạnh \(2a\). Tìm độ dài của véc tơ \(\overrightarrow{u} = \overrightarrow{MA} +
\overrightarrow{MB} + \overrightarrow{MC}.\)
Toàn bộ nội dung đã sẵn sàng! Nhấn Tải về để tải đầy đủ tài liệu.
-----------------------------------------------------
Như vậy, việc hiểu và áp dụng cách tính độ dài vectơ trong Toán học không chỉ giúp bạn giải quyết các bài toán lớp 10 mà còn mở ra nhiều ứng dụng trong các lĩnh vực khoa học và kỹ thuật. Việc thành thạo kỹ năng này sẽ là nền tảng vững chắc để bạn tiếp tục học các kiến thức nâng cao hơn về vectơ trong các lớp học sau này. Hãy luyện tập thật nhiều với các bài toán thực tế để nắm vững công thức và phương pháp tính độ dài vectơ. Đừng quên rằng sự thành công trong học tập phụ thuộc vào sự kiên trì và sáng tạo trong việc giải quyết vấn đề!
