Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm
Đóng
Điểm danh hàng ngày
  • Hôm nay +3
  • Ngày 2 +3
  • Ngày 3 +3
  • Ngày 4 +3
  • Ngày 5 +3
  • Ngày 6 +3
  • Ngày 7 +5
Bạn đã điểm danh Hôm nay và nhận 3 điểm!
Nhắn tin Zalo VNDOC để nhận tư vấn mua gói Thành viên hoặc tải tài liệu Hotline hỗ trợ: 0936 120 169
VnDoc.com Lớp 10 Toán lớp 10 Chuyên đề Toán 10
Đóng
Bạn đã dùng hết 1 lần làm bài Trắc nghiệm miễn phí. Mời bạn mua tài khoản VnDoc PRO để tiếp tục! Tìm hiểu thêm
Mua VnDoc PRO chỉ từ 79.000đ

Trắc nghiệm Bài tập thực tế ứng dụng hệ thức lượng trong tam giác

Bài tập Toán 10 có đáp án

Bài toán thực tế tam giác toán 10 - Có đáp án

Trong chương trình Toán 10, chủ đề Tam giác và hệ thức lượng là nội dung quan trọng giúp học sinh hiểu mối quan hệ giữa các cạnh, góc và ứng dụng vào các tình huống thực tế. Bài viết này tổng hợp trắc nghiệm Bài tập thực tế ứng dụng hệ thức lượng trong tam giác kèm đáp án chi tiết, giúp bạn vận dụng linh hoạt công thức và rèn luyện khả năng tư duy logic. Đây là tài liệu nằm trong chuyên mục Bài tập Toán 10 Tam giác có đáp án, được biên soạn bám sát chương trình học, hỗ trợ học sinh ôn tập hiệu quả và làm quen với các dạng bài ứng dụng thực tế trong tam giác.

Nhận biết Thông hiểu Vận dụng Vận dụng cao
  • Bài kiểm tra này bao gồm 13 câu
  • Điểm số bài kiểm tra: 13 điểm
  • Xem lại kỹ lý thuyết trước khi làm bài
  • Chuẩn bị giấy và bút để nháp trước khi bắt đầu
Bắt đầu!!
00:00:00
  • Câu 1: Thông hiểu
    Tính khoảng cách AB

    Khoảng cách từ A đến B không thể đo trực tiếp được vì phải qua một đầm lầy. Người ta xác định được một điểm C mà từ đó có thể nhìn được A và B dưới một góc 78^{o}24'. Biết CA = 250m,CB = 120m. Khoảng cách AB bằng bao nhiêu?

    Hướng dẫn:

    Ta có:

    AB^{2} = CA^{2} + CB^{2} -2CB.CA.\cos C

    = 250^{2} + 120^{2} -2.250.120.\cos78^{o}24' \simeq 64835

    \Rightarrow AB \simeq 255.

  • Câu 2: Thông hiểu
    Tính khoảng cách AB

    Khoảng cách từ A đến B không thể đo trực tiếp được vì phải qua một đầm lầy. Người ta xác định được một điểm C mà từ đó có thể nhìn được A và B dưới một góc 56^{0}16'. Biết CA = 200m;CB = 180m. Khoảng cách AB bằng bao nhiêu?

    Hướng dẫn:

    Ta có:

    AB^{2} = CA^{2} + CB^{2} -2CB.CA.\cos\widehat{C}

    = 200^{2} + 180^{2} -2.200.180.\cos56^{0}16' \approx 32416

    \Rightarrow AB = 180m

  • Câu 3: Vận dụng
    Tính chiều cao tòa nhà

    Trên nóc một tòa nhà có một cột ăng-ten cao 5\ m . Từ vị trí quan sát A cao 7\ m so với mặt đất, có thể nhìn thấy đỉnh B và chân C của cột ăng-ten dưới góc 50^{0} và 40^{0} so với phương nằm ngang.

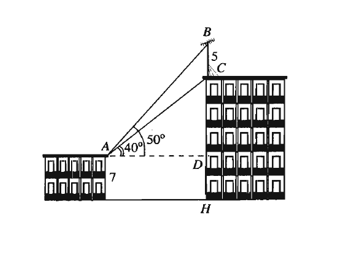
    Chiều cao của tòa nhà gần nhất với giá trị nào sau đây?

    Hướng dẫn:

    Từ hình vẽ, suy ra \widehat{BAC} = 10^{0} và

    \widehat{ABD} = 180^{0} - \left( \widehat{BAD} + \widehat{ADB} \right) = 180^{0} - \left( 50^{0} + 90^{0} \right) = 40^{0}.

    Áp dụng định lí sin trong tam giác ABC, ta có

    \frac{BC}{\sin\widehat{BAC}} = \frac{AC}{\sin\widehat{ABC}}

    \Rightarrow AC =\frac{BC.\sin\widehat{ABC}}{\sin\widehat{BAC}} =\frac{5.\sin40^{0}}{\sin10^{0}} \approx 18,5 m.

    Trong tam giác vuông ADC, ta có \sin\widehat{CAD} = \frac{CD}{AC}

    \Rightarrow CD = AC.\sin\widehat{CAD} =11,9\ m.

    Vậy CH = CD + DH = 11,9 + 7 = 18,9\ m.

  • Câu 4: Vận dụng
    Chọn đáp án thích hợp

    Để đo khoảng cách từ một điểm A trên bờ sông đến gốc cây C trên cù lao giữa sông, người ta chọn một điểm B cùng ở trên bờ với A sao cho từ A và B có thể nhìn thấy điểm C. Ta đo được khoảng cách AB = 40m, \widehat{CAB} = 45^{0} và \widehat{CBA} = 70^{0}.

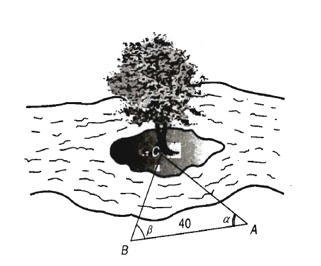
    Vậy sau khi đo đạc và tính toán được khoảng cách AC gần nhất với giá trị nào sau đây?

    Hướng dẫn:

    Áp dụng định lí sin vào tam giác ABC, ta có \frac{AC}{\sin B} = \frac{AB}{\sin C}

    Vì \sin C = \sin(\alpha + \beta) nên AC = \frac{AB.\sin\beta}{\sin(\alpha +\beta)} = \frac{40.\sin70^{0}}{\sin115^{0}} \approx 41,47\ m.

  • Câu 5: Vận dụng
    Tính bán kính chiếc đĩa

    Trong khi khai quật một ngôi mộ cổ, các nhà khảo cổ học đã tìm được một chiếc đĩa cổ hình tròn bị vỡ, các nhà khảo cổ muốn khôi phục lại hình dạng chiếc đĩa này. Để xác định bán kính của chiếc đĩa, các nhà khảo cổ lấy 3 điểm trên chiếc đĩa và tiến hành đo đạc thu được kết quả như hình vẽ (AB = 4,3cm,BC = 3,7cm, CA = 7,5cm). Bán kính của chiếc đĩa này bằng.

    Hướng dẫn:

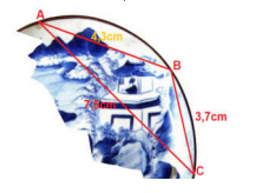
    Bán kính R của chiếc đĩa bằng bán kính đường tròn ngoại tiếp tam giác ABC.

    Nửa chu vi của tam giác là:

    p = \frac{AB + AC + BC}{2} = \frac{4,3 + 3,7 + 7,5}{2} = \frac{31}{4}(cm)

    Diện tích tam giác là:

    S = \sqrt{p(p - a)(p - b)(p - c)} = 5,2\left( cm^{2} \right).

    Mà S = \frac{AB.BC.CA}{4R} \Rightarrow R = \frac{AB.BC.CA}{4S} = 5,73(cm).

  • Câu 6: Thông hiểu
    Tính khoảng cách AB

    Từ một đỉnh tháp chiều cao CD = 80m, người ta nhìn hai điểm A và B trên mặt đất dưới các góc nhìn là 72^{0}12' và 34^{0}26'. Ba điểm A; B; D thẳng hàng. Tính khoảng cách AB?

    Hướng dẫn:

    Ta có: Trong tam giác vuông :

    \tan72^{0}12' =\frac{CD}{AD}\Rightarrow AD =\frac{CD}{\tan72^{0}12'} \approx 25,7

    Trong tam giác vuông :

    \tan34^{0}12' =\frac{CD}{BD}\Rightarrow BD =\frac{CD}{\tan34^{0}12'} \approx 116,7

    Suy ra: khoảng cách AB = 116,7 - 25,7 = 91(m)

  • Câu 7: Vận dụng
    Tính khoảng cách hai tàu sau 2 giờ

    Hai chiếc tàu thuỷ cùng xuất phát từ vị trí A, đi thẳng theo hai hướng tạo với nhau một góc 60^{0}. Tàu thứ nhất chạy với tốc độ 30\ km/h, tàu thứ hai chạy với tốc độ 40\ km/h. Hỏi sau 2 giờ hai tàu cách nhau bao nhiêu km?

    Hướng dẫn:

    Sau 2h quãng đường tàu thứ nhất chạy được là: S_{1} = 30.2 = 60\ km.

    Sau 2h quãng đường tàu thứ hai chạy được là: S_{2} = 40.2 = 80\ km.

    Vậy sau 2h hai tàu cách nhau là:

    S = \sqrt{{S_{1}}^{2} + {S_{2}}^{2} -2S_{1}.S_{2}.\cos60^{0}} = 20\sqrt{13}.

  • Câu 8: Vận dụng
    Chọn đáp án gần nhất với kết quả đúng

    Hai chiếc tàu thủy cùng xuất phát từ một vị trí A, đi thẳng theo hai hướng tạo với nhau góc 60^{0}. Tàu B chạy với tốc độ 20 hải lí một giờ. Tàu C chạy với tốc độ 15 hải lí một giờ. Sau hai giờ, hai tàu cách nhau bao nhiêu hải lí?

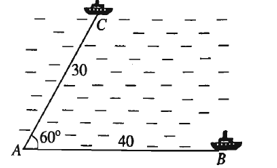
    Kết quả gần nhất với số nào sau đây?

    Hướng dẫn:

    Sau 2 giờ tàu B đi được 40 hải lí, tàu C đi được 30 hải lí.

    Vậy tam giác ABC có AB = 40,\ \ \ AC = 30 và \widehat{A} = 60^{0}.

    Áp dụng định lí côsin vào tam giác ABC, ta có

    a^{2} = b^{2} + c^{2} - 2bc\cos A =30^{2} + 40^{2} - 2.30.40.\cos60^{0}

    = 900 + 1600 - 1200 = 1300.

    Vậy BC = \sqrt{1300} \approx 36 (hải lí).

    Sau 2 giờ, hai tàu cách nhau khoảng 36 hải lí.

  • Câu 9: Vận dụng cao
    Câu 12: Chọn đáp án đúng

    Từ hai vị trí A và B của một tòa nhà, người ta quan sát đỉnh C của ngọn núi. Biết rằng độ cao AB = 70m, phương nhìn AC tạo với phương nằm ngang góc 30^{0}, phương nhìn BC tạo với phương nằm ngang góc 15^{0}30'.

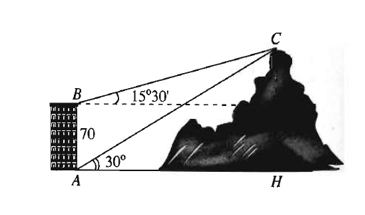
    Ngọn núi đó có độ cao so với mặt đất gần nhất với giá trị nào sau đây?

    Hướng dẫn:

    Từ giả thiết, ta suy ra tam giác ABC có \widehat{CAB} = 60^{0},\ \ \widehat{ABC} = 105^{0}30' và c = 70.

    Khi đó \widehat{A} + \widehat{B} + \widehat{C} = 180^{0}

    \Leftrightarrow \widehat{C} = 180^{0} - \left( \widehat{A} + \widehat{B} \right) = 180^{0} - 165^{0}30' = 14^{0}30'.

    Theo định lí sin, ta có \frac{b}{\sin B} = \frac{c}{\sin C} hay \frac{b}{sin105^{0}30'} = \frac{70}{sin14^{0}30'}

    Do đó AC = b = \frac{70.sin105^{0}30'}{sin14^{0}30'} \approx 269,4\ m

    Gọi CH là khoảng cách từ C đến mặt đất.

    Tam giác vuông ACH có cạnh CH đối diện với góc 30^{0} nên CH = \frac{AC}{2} = \frac{269,4}{2} = 134,7\ \ m.

    Vậy ngọn núi cao khoảng 135\ m.

  • Câu 10: Thông hiểu
    Tính khoảng cách AB

    Khoảng cách từ A đến B không thể đo trực tiếp được vì phải qua một đầm lầy. Người ta xác định được một điểm Cmà từ đó có thể nhìn được A và Bdưới một góc 56^{0}16'. Biết CA = 200\ m, CB = 180\ m. Khoảng cách AB bằng bao nhiêu?

    Hướng dẫn:

    Ta có:

    AB^{2} = CA^{2} + CB^{2} -2CB.CA.\cos C

    = 200^{2} + 180^{2} -2.200.180.\cos56^{0}16' \simeq 32416

    \Rightarrow AB \simeq 180.

  • Câu 11: Thông hiểu
    Chọn đáp án đúng

    Xác định chiều cao của một tháp mà không cần lên đỉnh của tháp. Đặt kế giác thẳng đứng cách chân tháp một khoảng CD = 60m, giả sử chiều cao của giác kế là OC = 1m.

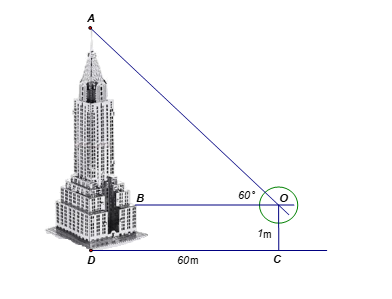
    Quay thanh giác kế sao cho khi ngắm theo thanh ta nhìn thấy đỉnh A của tháp. Đọc trên giác kế số đo của góc \widehat{AOB} = 60^{0}. Chiều cao của ngọn tháp gần với giá trị nào sau đây:

    Hướng dẫn:

    Tam giác OAB vuông tại B, có:

    \tan\widehat{AOB} = \frac{AB}{OB}\Rightarrow AB = \tan60^{0}.OB =60\sqrt{3}m.

    Vậy chiếu cao của ngọn tháp là: h = AB + OC = \left( 60\sqrt{3} + 1 \right)\ m.

  • Câu 12: Vận dụng
    Tính chiều cao của cây

    Từ vị trí A người ta quan sát một cây cao (hình vẽ).

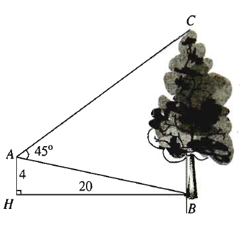
    Biết AH = 4m,\ HB = 20m,\ \widehat{BAC} = 45^{0}. Chiều cao của cây gần nhất với giá trị nào sau đây?

    Hướng dẫn:

    Trong tam giác AHB, ta có:

    \tan\widehat{ABH} = \frac{AH}{BH} = \frac{4}{20} = \frac{1}{5}

    \Rightarrow \widehat{ABH} \approx 11^{0}19'.

    Suy ra \widehat{ABC} = 90^{0} - \widehat{ABH} = 78^{0}41'.

    Suy ra \widehat{ACB} = 180^{0} - \left( \widehat{BAC} + \widehat{ABC} \right) = 56^{0}19'.

    Áp dụng định lý sin trong tam giác ABC, ta được

    \frac{AB}{\sin\widehat{ACB}} = \frac{CB}{\sin\widehat{BAC}}\Rightarrow CB =\frac{AB.\sin\widehat{BAC}}{\sin\widehat{ACB}} \approx 17m.

  • Câu 13: Thông hiểu
    Tính chiều cao ngọn tháp

    Giả sử CD = h là chiều cao của tháp trong đó C là chân tháp. Chọn hai điểm A,\ B trên mặt đất sao cho ba điểm A,\ B và C thẳng hàng. Ta đo được AB = 24\ m, \widehat{CAD} = 63^{0},\ \widehat{CBD} = 48^{0}.

    Chiều cao h của tháp gần với giá trị nào sau đây?

    Hướng dẫn:

    Áp dụng định lí sin vào tam giác ABD, ta có:

    \frac{AD}{\sin\beta} = \frac{AB}{\sin D}.

    Ta có \alpha = \widehat{D} + \beta nên \widehat{D} = \alpha - \beta = 63^{0} - 48^{0} = 15^{0}.

    Do đó AD = \frac{AB.\sin\beta}{\sin(\alpha- \beta)} = \frac{24.\sin48^{0}}{\sin15^{0}} \approx 68,91m.

    Trong tam giác vuông ACD, có h = CD = AD.\sin\alpha \approx 61,4m

0/13
13 câu:
Kiểm tra Kiểm tra lại Bỏ qua Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Kết quả làm bài:
  • Nhận biết (46%):
    2/3
  • Thông hiểu (46%):
    2/3
  • Vận dụng (8%):
    2/3
  • Thời gian làm bài: 00:00:00
  • Số câu làm đúng: 0
  • Số câu làm sai: 0
  • Điểm số: 0
  • Điểm thưởng: 0
Làm lại
Bạn còn 1 lượt làm bài tập miễn phí. Hãy mua tài khoản VnDoc PRO để học không giới hạn nhé! Bạn đã HẾT lượt làm bài tập miễn phí! Hãy mua tài khoản VnDoc PRO để làm Trắc nghiệm không giới hạn và tải tài liệu nhanh nhé! Mua ngay
1
3 Bài viết đã được lưu
Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!
Số điện thoại này đã được xác thực!
Bạn có thể dùng Sđt này đăng nhập tại đây!
Lỗi gửi SMS, liên hệ Admin
Sắp xếp theo
Xóa Đăng nhập để Gửi
Tìm bài trong mục này
🖼️

Chuyên đề Toán 10
Xem thêm