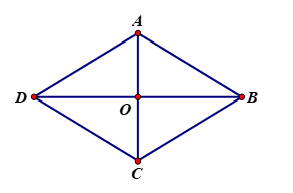
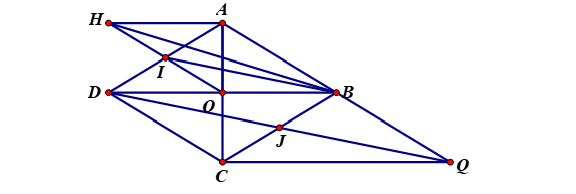
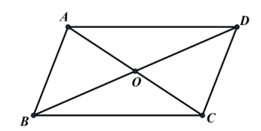
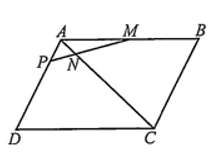
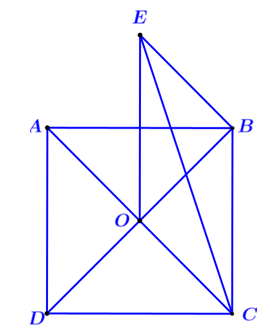
Cho hình bình hành có tâm
.
lần lượt là trung điểm của các cạnh
. Xét tính đúng, sai của các phát biểu sau.
a) . Sai||Đúng
b) . Sai||Đúng
c) . Đúng||Sai
d) với
là trung điểm của
. Sai||Đúng
Cho hình bình hành có tâm
.
lần lượt là trung điểm của các cạnh
. Xét tính đúng, sai của các phát biểu sau.
a) . Sai||Đúng
b) . Sai||Đúng
c) . Đúng||Sai
d) với
là trung điểm của
. Sai||Đúng
Tổng quan đáp án:
a) Saib) Saic) Đúngd) Sai
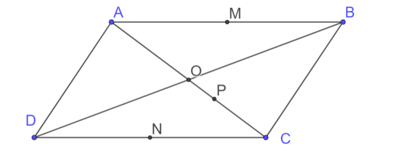
Hình vẽ minh họa:
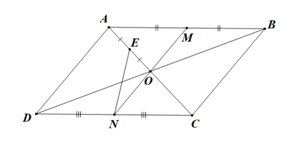
a) Vì là trung điểm của
nên
và hai vectơ
ngược hướng nên
.
b) Theo quy tắc hình bình hành: .
c) .
d) Ta có:
.