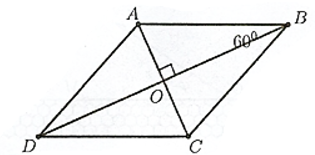
Trong mặt phẳng tọa độ cho tam giác
có
,
và
a) Tích vô hướng của hai véc tơ là một số. Đúng||Sai
b) . Sai||Đúng
c) vuông góc với trục
. Đúng||Sai
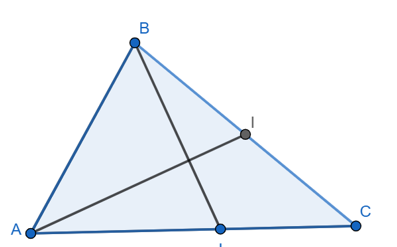
d) Gọi là trực tâm của tam giác đã cho. Tính được giá trị biểu thức
. Sai||Đúng
Trong mặt phẳng tọa độ cho tam giác
có
,
và
a) Tích vô hướng của hai véc tơ là một số. Đúng||Sai
b) . Sai||Đúng
c) vuông góc với trục
. Đúng||Sai
d) Gọi là trực tâm của tam giác đã cho. Tính được giá trị biểu thức
. Sai||Đúng
|
a) Đúng |
b) Sai |
c) Đúng |
d) Sai |
a) Tích vô hướng của hai vectơ là một số.
b) Ta có:
c) .
Vậy vuông góc với trục
.
d) Gọi là trực tâm của tam giác đã cho.
Ta có:
Vì là trực tâm tam giác
nên:
Suy ra .