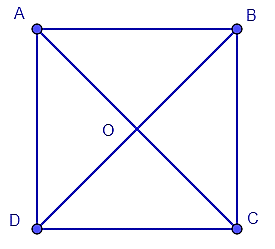
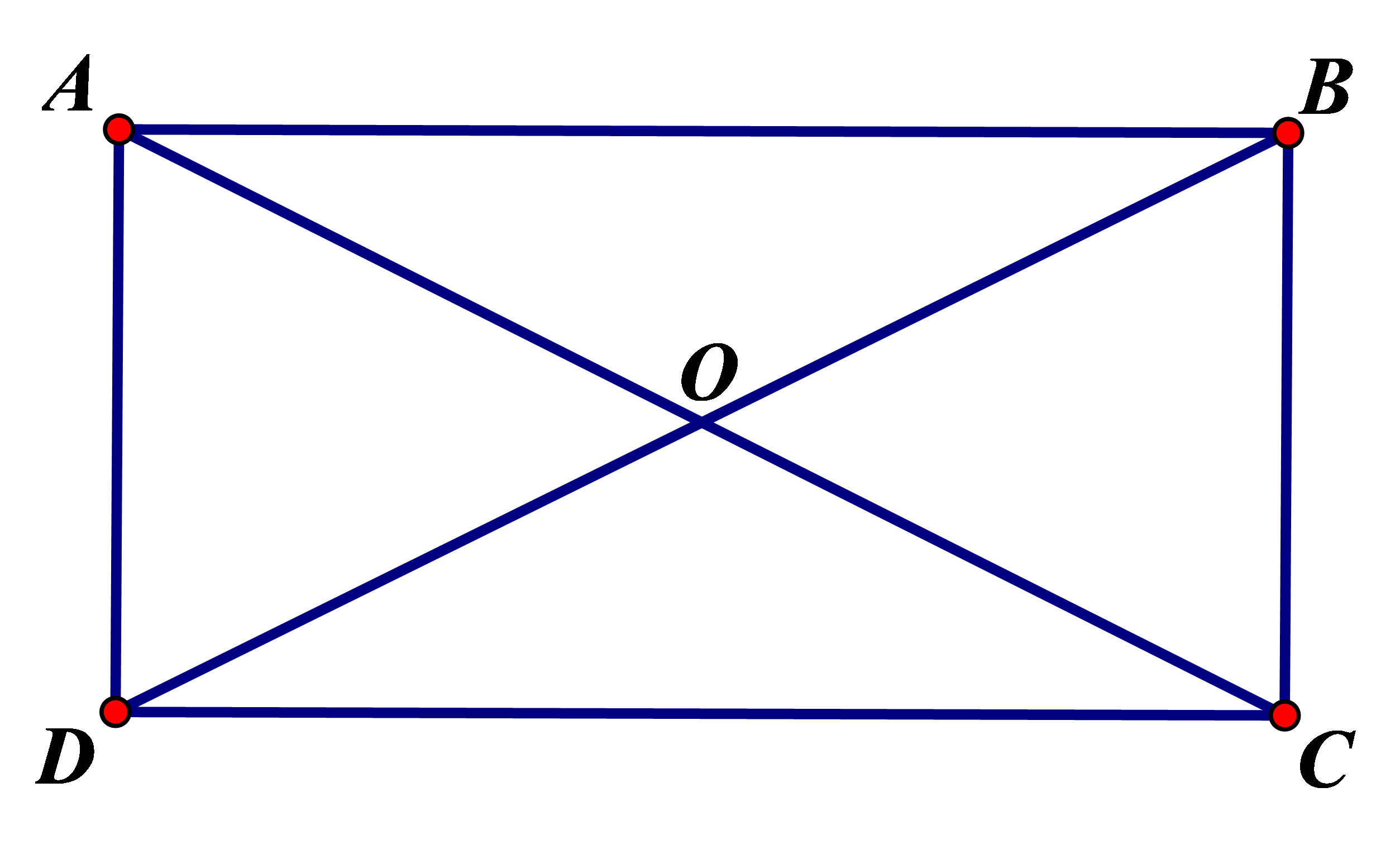
Cho là hình vuông tâm
.
a) . Đúng||Sai
b) . Đúng||Sai
c) . Đúng||Sai
d) Tập hợp điểm thỏa mãn đẳng thức:
là một điểm. Sai||Đúng
Cho là hình vuông tâm
.
a) . Đúng||Sai
b) . Đúng||Sai
c) . Đúng||Sai
d) Tập hợp điểm thỏa mãn đẳng thức:
là một điểm. Sai||Đúng
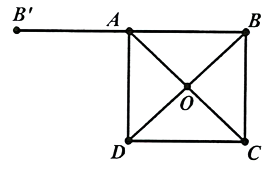
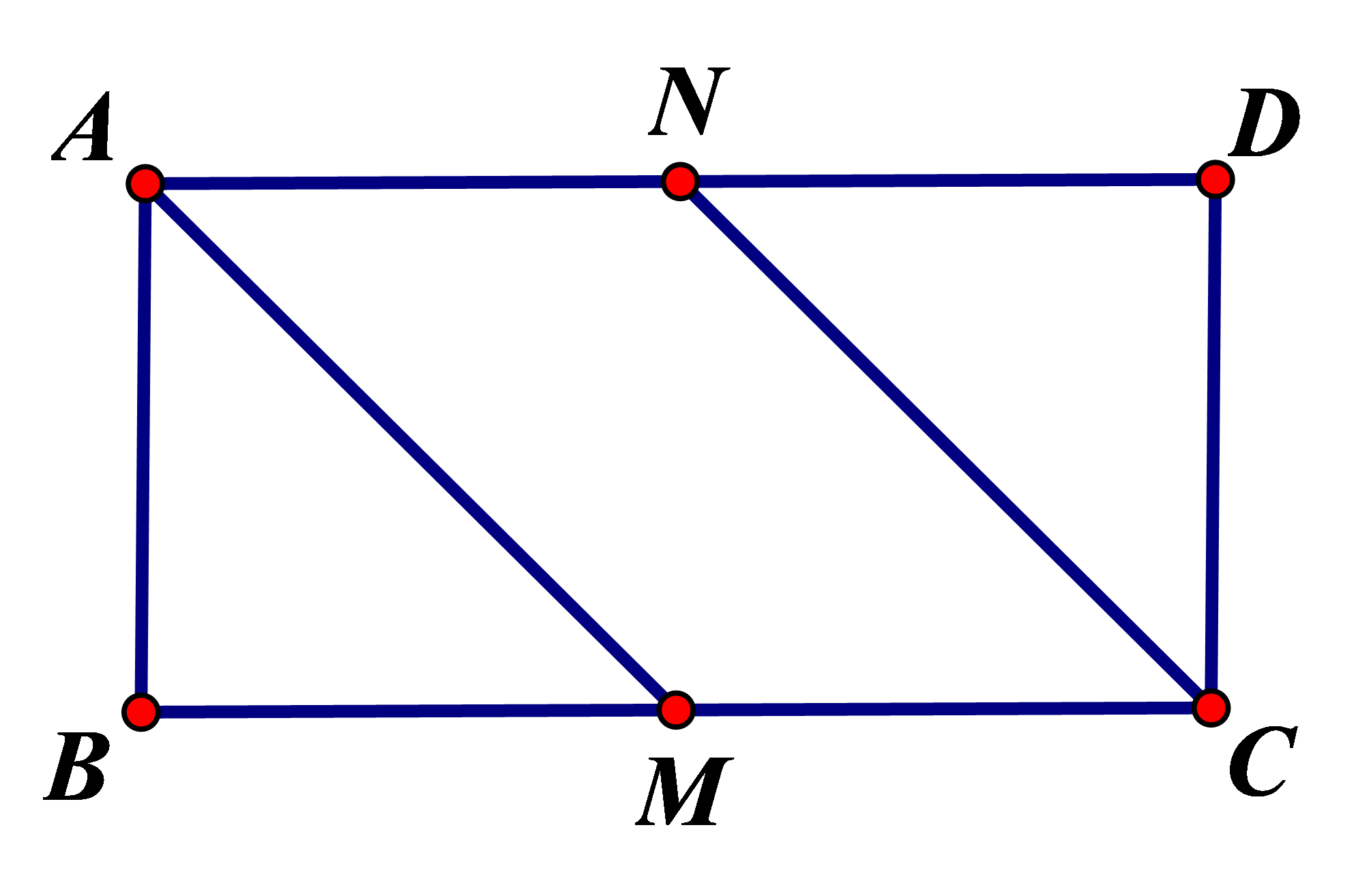
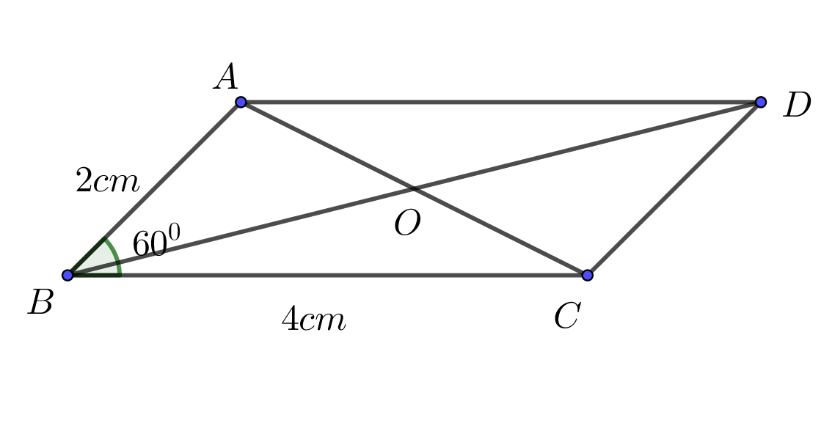
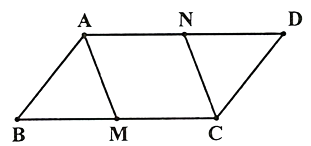
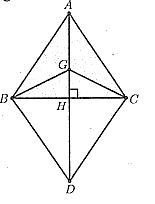
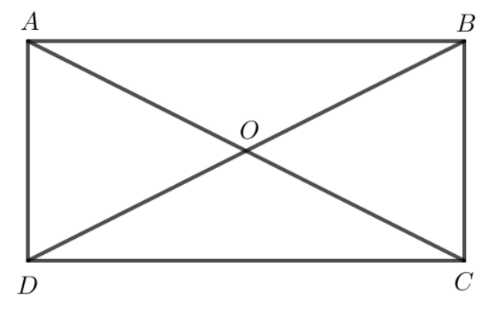
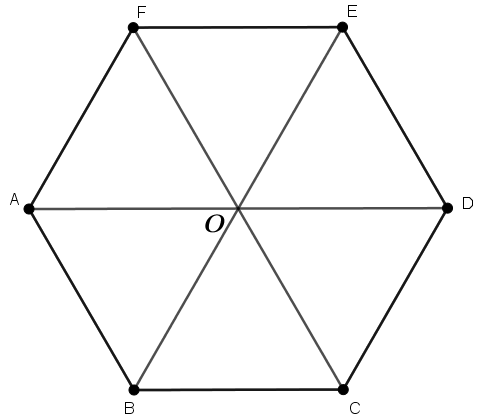
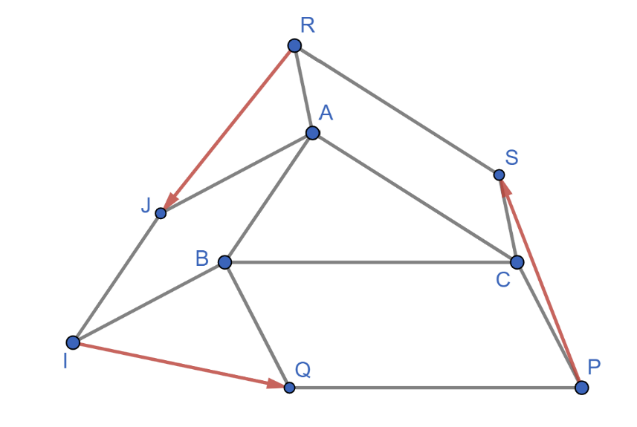
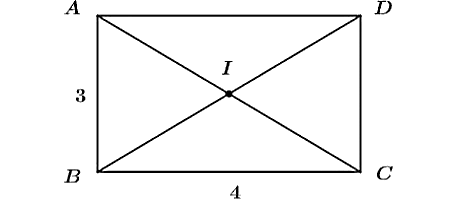
Hình vẽ minh họa
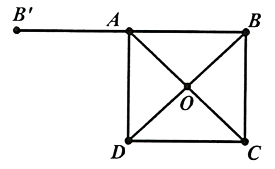
Ta có là hình vuông tâm
suy ra
. Đúng
Ta có , khi đó
. Đúng
Ta có suy ra
Đúng.
.
Khi đó, .
Vậy tập hợp điểm là đường tròn tâm
bán kính
. Sai.