Tam giác vuông ở
và có
Tính
Hình vẽ minh họa:
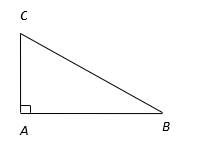
Xác định được
Ta có
Vậy
Trong chương trình Toán 10, chuyên đề Vectơ là nền tảng quan trọng giúp học sinh nắm vững các kiến thức hình học không gian. Bài viết này tổng hợp trắc nghiệm Góc giữa hai vectơ Toán 10 có đáp án chi tiết, giúp bạn củng cố kiến thức, luyện tập kỹ năng tính toán và làm quen với các dạng bài thường gặp trong đề kiểm tra, đề thi học kỳ. Cùng ôn tập hiệu quả với bộ bài tập trắc nghiệm Vectơ Toán 10 được biên soạn bám sát chương trình học nhé!
Tam giác vuông ở
và có
Tính
Hình vẽ minh họa:

Xác định được
Ta có
Vậy
Cho tam giác đều Tính
?
Ta có:
Cho hai vectơ và
có
,
và
. Khi đó cosin của góc giữa hai vectơ
và
bằng:
Hình vẽ minh họa:
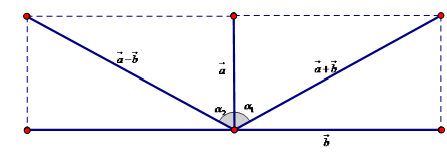
Nhận thấy suy ra
Mặt khác: .
Do đó góc giữa hai vectơ và
bằng
Vậy
Cho hai vectơ và
khác
. Xác định góc
giữa hai vectơ
và
khi
Ta có .
Mà theo giả thiết , suy ra
Tính biết
, (
;
)
Ta có:
Cho tam giác đều Tính
Hình vẽ minh họa:
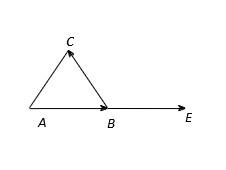
Vẽ .
Khi đó
.
Tương tự, ta cũng có
.
Vậy .
Cho hình vuông . Tính
.
Hình vẽ minh họa:
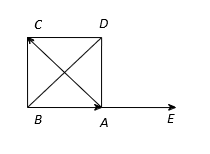
Vẽ .
Khi đó
Cho hai vectơ và
thỏa mãn
và
Xác định góc
giữa hai vectơ
và
Ta có:
Tam giác vuông ở
và có góc
. Hệ thức nào sau đây sai?
Ta có:
Cho hình vuông tâm
Tính tổng
?
Hình vẽ minh họa:
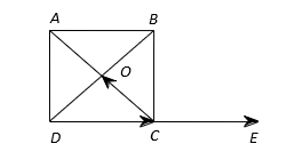
Ta có cùng hướng nên
.
Ta có ngược hướng nên
Vẽ , khi đó
Vậy
Cho hai vectơ và
thỏa mãn
và hai vectơ
và
vuông góc với nhau. Xác định góc
giữa hai vectơ
và
Ta có:
Suy ra
Cho là tâm đường tròn ngoại tiếp tam giác đều
. Góc nào sau đây bằng
?
Hình vẽ minh họa:
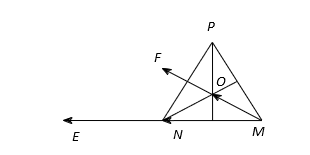
Vẽ .
Khi đó
.
Vẽ . Khi đó
Vì .
Ta có .
Cho tam giác . Tính tổng
Ta có
Cho tam giác đều có đường cao
. Tính
Hình vẽ minh họa
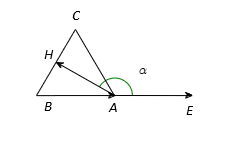
Vẽ .
Khi đó (hình vẽ)
.
Cho tam giác với
. Tính tổng
.
Ta có
Tam giác có góc
bằng
và có trực tâm
Tính tổng
.
Hình vẽ minh họa:
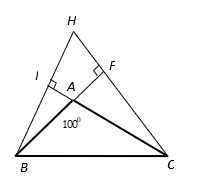
Ta có
.(do tứ giác
nội tiếp)
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây: