Cho là tam giác đều. Mệnh đề nào sau đây đúng?
Phương án : Do
nên loại.
Phương án :
nên loại.
Phương án : Do
và
không cùng phương nên loại.
Phương án :
,
nên chọn.
Trong chuyên đề Vectơ Toán 10, phần tích vô hướng giữa hai vectơ là nội dung quan trọng giúp học sinh vận dụng linh hoạt kiến thức vào giải bài tập hình học và đại số. Bài viết này cung cấp trắc nghiệm tích vô hướng giữa hai vectơ (mức độ thông hiểu – vận dụng) kèm đáp án chi tiết, giúp bạn rèn luyện kỹ năng tính toán, phân tích và ứng dụng công thức tích vô hướng vào các bài toán thực tế. Đây là bộ bài tập Toán 10 tích vô hướng có đáp án giúp học sinh chuẩn bị tốt cho các kỳ kiểm tra và ôn thi học kỳ.
Cho là tam giác đều. Mệnh đề nào sau đây đúng?
Phương án : Do
nên loại.
Phương án :
nên loại.
Phương án : Do
và
không cùng phương nên loại.
Phương án :
,
nên chọn.
Cho tam giác đều cạnh bằng
. Tập hợp các điểm
thỏa mãn đẳng thức
nằm trên một đường tròn
có bán kính
. Tính
.
Hình vẽ minh họa:
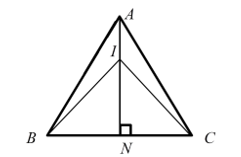
Gọi là trung điểm đoạn
.
Gọi là điểm thỏa:
, nên điểm
thuộc đoạn thẳng
sao cho
.
Khi đó: , và
.
.
Ta có:
.
.
Cho tam giác có cạnh
và đường cao
,
ở trên cạnh
sao cho
. Tính
Ta có:
.
Cho ba điểm không thẳng hàng. Điều kiện cần và đủ để tích vô hướng
là:
Ta có :
Cho hai điểm cố định có khoảng cách bằng
. Tập hợp các điểm
thỏa mãn
là:
Gọi là điểm đối xứng của
qua
. Khi đó
Suy ra
Kết hợp với giả thiết, ta có:
.
Vậy tập hợp các điểm là đường thẳng qua
và vuông góc với
Cho hình chữ nhật có
Đẳng thức nào sau đây đúng?
Giả thiết không cho góc, ta phân tích các vectơ theo các vectơ có giá vuông góc với nhau.
Ta có:
.
Cho tam giác . Tập hợp các điểm
thỏa mãn
là:
Ta có:
Vậy tập hợp các điểm là đường thẳng đi qua
và vuông góc với
Cho hai điểm cố định và
. Tập hợp các điểm
thỏa mãn
là:
Gọi là trung điểm của
, ta có:
.
Theo bài ra ta có:
.
Vậy điểm .
Kết luận: Tập hợp các điểm thỏa mãn
là một điểm.
Cho tam giác đều cạnh
. Tập hợp các điểm
thỏa mãn đẳng thức
là:
Hình vẽ minh họa
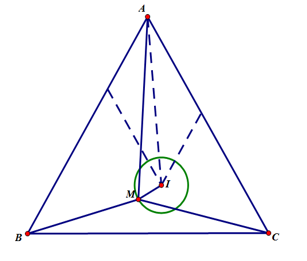
Ta có .
Dựng điểm thỏa mãn
.
Khi đó:
.
Do đó tập hợp các điểm là đường tròn cố định có bán kính
.
Cho hai vectơ và
. Đẳng thức nào sau đây sai?
Nhận thấy và
chỉ khác nhau về hệ số
và
nên thử kiểm tra đáp án
và
.
Ta có :
Chọn
Đáp án đúng, vì
Đáp án đúng, vì
Tìm tập các hợp điểm thỏa mãn
với
là ba đỉnh của tam giác.
Gọi là trọng tâm tam giác
Suy ra
Ta có:
Biểu thức chứng tỏ
hay
nhìn đoạn
dưới một góc vuông nên tập hợp các điểm
là đường tròn đường kính
Cho tam giác có
Gọi
là trung điểm cạnh
Đẳng thức nào sau đây đúng?
Vì là trung điểm của
suy ra
Khi đó:
Cho tam giác đều cạnh
, với các đường cao
vẽ
Cho các khẳng định sau:
a) .
b) .
c) .
Có bao nhiêu câu nào sau đây đúng?
Khẳng định a):
nên đẳng thức ở phương án A là đúng.
Khẳng định b):
nên đẳng thức ở phương án B là đúng.
Khẳng định c):
nên đẳng đúng
Vậy cả 3 khẳng định đều đúng.
Cho hai điểm phân biệt. Tập hợp những điểm
thỏa mãn
là:
Ta có:
.
Tập hợp điểm là đường tròn đường kính
.
Cho hình vuông cạnh
Đẳng thức nào sau đây đúng?
Ta có nên
Cho hình thang vuông có đáy lớn
, đáy nhỏ
, đường cao
;
là trung điểm của
. Câu nào sau đây sai?
Phương án :
nên loại.
Phương án :
suy ra
nên loại.
Phương án :
suy ra
nên loại.
Phương án :
không vuông góc với
suy ra
nên chọn.
Cho hình vuông cạnh
Mệnh đề nào sau đây sai?
Ta đi tính tích vô hướng ở vế trái của 4 phương án.
Phương án :
nên loại.
Phương án :
nên loại.
Phương án :
nên chọn.
Cho hình thoi có
và
. Đẳng thức nào sau đây đúng?
Hình vẽ minh họa:
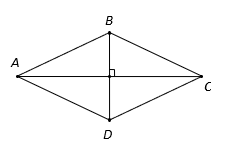
Gọi , giả thiết không cho góc, ta phân tích các vectơ
theo các vectơ có giá vuông góc với nhau.
Ta có:
.
Cho hình thang vuông có đáy lớn
, đáy nhỏ
, đường cao
;
là trung điểm của
. Khi đó
bằng:
Ta có:
.
Cho hình vuông cạnh
. Gọi
là điểm đối xứng của
qua
Đẳng thức nào sau đây đúng?
Hình vẽ minh họa:
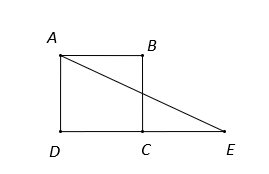
Ta có là trung điểm của
nên
Khi đó:
Cho hình vuông cạnh
. Hỏi mệnh đề nào sau đây sai?
Phương án :
Do nên loại.
Phương án :
Do nên chọn.
Cho ba điểm phân biệt. Tập hợp những điểm
mà
là:
Ta có:
.
Tập hợp điểm là đường thẳng đi qua
và vuông góc với
.
Cho hai điểm cố định và
Tập hợp các điểm
thỏa mãn
là:
Gọi là trung điểm của đoạn thẳng
Ta có:
Theo giả thiết, ta có
Tam giác vuông ở
và có góc
. Hệ thức nào sau đây là sai?
Phương án :
nên loại.
Phương án :
nên loại.
Phương án :
nên loại .
Phương án :
nên chọn.
Cho tam giác đều cạnh
, với các đường cao
vẽ
Câu nào sau đây đúng?
Phương án :
Do nên loại
Phương án :
Do nên loại
Phương án :
Do nên chọn.
Cho hình chữ nhật có
và
. Gọi
là trung điểm của cạnh
. Đẳng thức nào sau đây đúng?
Hình vẽ minh họa :
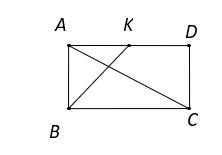
Ta có:
Ta có:
(vì
nhọn).
Mặt khác góc giữa hai vectơ là góc ngoài của góc
Suy ra
Cho hình vuông tâm
. Hỏi mệnh đề nào sau đây sai?
Phương án :
suy ra
nên loại.
Phương án :
và
suy ra
nên loại.
Phương án :
.
nên chọn.
Cho là bốn điểm tùy ý. Trong các hệ thức sau, hệ thức nào sai?
Đáp án đúng theo tính chất phân phối.
Đáp án sai. Sửa lại cho đúng
.
Đáp án đúng theo tính chất giao hoán.
Đáp án đúng theo tính chất phân phối.
Cho hình vuông cạnh bằng
Điểm
nằm trên đoạn thẳng
sao cho
. Gọi
là trung điểm của đoạn thẳng
Đẳng thức nào sau đây đúng?
Hình vẽ minh họa:
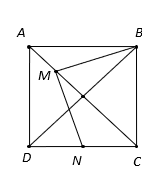
Giả thiết không cho góc, ta phân tích các vectơ theo các vectơ có giá vuông góc với nhau.
Suy ra:
.
Cho tam giác . Tập hợp các điểm
thỏa mãn
là:
Gọi là trung điểm
Ta có
.
Biểu thức chứng tỏ
hay
nhìn đoạn
dưới một góc vuông nên tập hợp các điểm
là đường tròn đường kính
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây: