Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm
Đóng
Điểm danh hàng ngày
  • Hôm nay +3
  • Ngày 2 +3
  • Ngày 3 +3
  • Ngày 4 +3
  • Ngày 5 +3
  • Ngày 6 +3
  • Ngày 7 +5
Bạn đã điểm danh Hôm nay và nhận 3 điểm!
Nhắn tin Zalo VNDOC để nhận tư vấn mua gói Thành viên hoặc tải tài liệu Hotline hỗ trợ: 0936 120 169
VnDoc.com Lớp 10 Toán lớp 10 Chuyên đề Toán 10
Đóng
Bạn đã dùng hết 1 lần làm bài Trắc nghiệm miễn phí. Mời bạn mua tài khoản VnDoc PRO để tiếp tục! Tìm hiểu thêm
Mua VnDoc PRO chỉ từ 79.000đ

Trắc nghiệm tích vô hướng giữa hai vectơ Toán 10 (mức độ nhận biết)

Bài tập Toán 10 Tích vô hướng có đáp án

Bài tập tích vô hướng giữa hai vectơ có đáp án

Trong chương trình Toán 10, chuyên đề tích vô hướng giữa hai vectơ đóng vai trò quan trọng giúp học sinh hiểu sâu hơn mối quan hệ giữa các vectơ trong hình học và đại số. Bài viết này tổng hợp trắc nghiệm tích vô hướng giữa hai vectơ Toán 10 (mức độ nhận biết) kèm đáp án chi tiết, giúp bạn củng cố kiến thức cơ bản, nắm vững công thức và cách vận dụng trong từng dạng bài. Đây là nguồn bài tập Toán 10 tích vô hướng có đáp án hữu ích cho quá trình ôn tập và kiểm tra.

Nhận biết Thông hiểu Vận dụng Vận dụng cao
  • Bài kiểm tra này bao gồm 24 câu
  • Điểm số bài kiểm tra: 24 điểm
  • Xem lại kỹ lý thuyết trước khi làm bài
  • Chuẩn bị giấy và bút để nháp trước khi bắt đầu
Bắt đầu!!
00:00:00
  • Câu 1: Nhận biết
    Chọn đáp án đúng

    Nếu hai điểm M, N thỏa mãn \overrightarrow{MN}.\ \overrightarrow{NM} = - 16 thì độ dài đoạn thẳng MN bằng bao nhiêu?

    Hướng dẫn:

    Ta có:

    \overrightarrow{MN}.\overrightarrow{NM} = \overrightarrow{MN}. ( - \overrightarrow{MN})= -MN^{2} = - 16 \Rightarrow MN = 4

  • Câu 2: Nhận biết
    Chọn đáp án đúng

    Cho tam giác ABC vuông cân tại A và có AB = AC = a. Tính \overrightarrow{AB}.\overrightarrow{BC}.

    Hướng dẫn:

    Xác định được góc \left( \overrightarrow{AB},\overrightarrow{BC} \right) là góc ngoài của góc \widehat{B} nên \left( \overrightarrow{AB},\overrightarrow{BC} \right) = 135^{0}

    Do đó \overrightarrow{AB}.\overrightarrow{BC} =AB.BC.\cos\left( \overrightarrow{AB},\overrightarrow{BC} \right)=a.a\sqrt{2}.\cos135^{0} = - a^{2}

  • Câu 3: Nhận biết
    Tìm biểu thức sai

    Cho M là trung điểm AB, tìm biểu thức sai?

    Hướng dẫn:

    Phương án \overrightarrow{MA}.\overrightarrow{AB} = - MA.AB: \overrightarrow{MA},\overrightarrow{AB} ngược hướng suy ra

    \overrightarrow{MA}.\overrightarrow{AB} =MA.AB.\cos180^{o} = - MA.AB nên loại \overrightarrow{MA}.\overrightarrow{AB} = - MA.AB.

    Phương án \overrightarrow{MA}.\overrightarrow{MB} = - MA.MB :\overrightarrow{MA},\overrightarrow{MB} ngược hướng suy ra

    \overrightarrow{MA}.\overrightarrow{MB} =MA.MB.\cos180^{o} = - MA.MB nên loại \overrightarrow{MA}.\overrightarrow{MB} = - MA.MB.

    Phương án \overrightarrow{AM}.\overrightarrow{AB} = AM.AB: \overrightarrow{AM},\overrightarrow{AB} cùng hướng suy ra

    \overrightarrow{AM}.\overrightarrow{AB} =AM.AB.\cos0^{o} = AM.AB nên loại \overrightarrow{AM}.\overrightarrow{AB} = AM.AB.

    Phương án \overrightarrow{MA}.\overrightarrow{MB} = MA.MB: \overrightarrow{MA},\overrightarrow{MB} ngược hướng suy ra

    \overrightarrow{MA}.\overrightarrow{MB} = MA.MB.\cos180^{o} = - MA.MB nên chọn \overrightarrow{MA}.\overrightarrow{MB} = MA.MB.

  • Câu 4: Nhận biết
    Tính tích vô hướng giữa hai vectơ

    Cho hình thang vuông ABCD có đáy lớn AB = 4a, đáy nhỏ CD = 2a, đường cao AD = 3a.Tính \overrightarrow{DA}.\overrightarrow{BC}  

    Hướng dẫn:

    Ta có:

    \overrightarrow{DA}.\overrightarrow{BC} = \overrightarrow{DA}.\left( \overrightarrow{BA} + \overrightarrow{AD} + \overrightarrow{DC} \right) = \overrightarrow{DA}.\overrightarrow{AD} = - 9a^{2}

  • Câu 5: Nhận biết
    Tìm mệnh đề sai

    Cho tam giác đều ABC có cạnh bằng a và chiều cao AH. Mệnh đề nào sau đây là sai?

    Hướng dẫn:

    Xác định được góc \left( \overrightarrow{AC},\overrightarrow{CB} \right) là góc ngoài của góc \widehat{A} nên \left( \overrightarrow{AC},\overrightarrow{CB} \right) = 120^{0}

    Do đó \overrightarrow{AC}.\overrightarrow{CB} =AC.CB.\cos\left( \overrightarrow{AC},\overrightarrow{CB} \right) =a.a.\cos120^{0} = - \frac{a^{2}}{2}

  • Câu 6: Nhận biết
    Tính tích vô hướng giữa hai vectơ

    Cho tam giác ABC vuông tại B, BC = a\sqrt{3}. Tính \overrightarrow{AC}.\overrightarrow{CB}?

    Hướng dẫn:

    Hình vẽ minh họa:

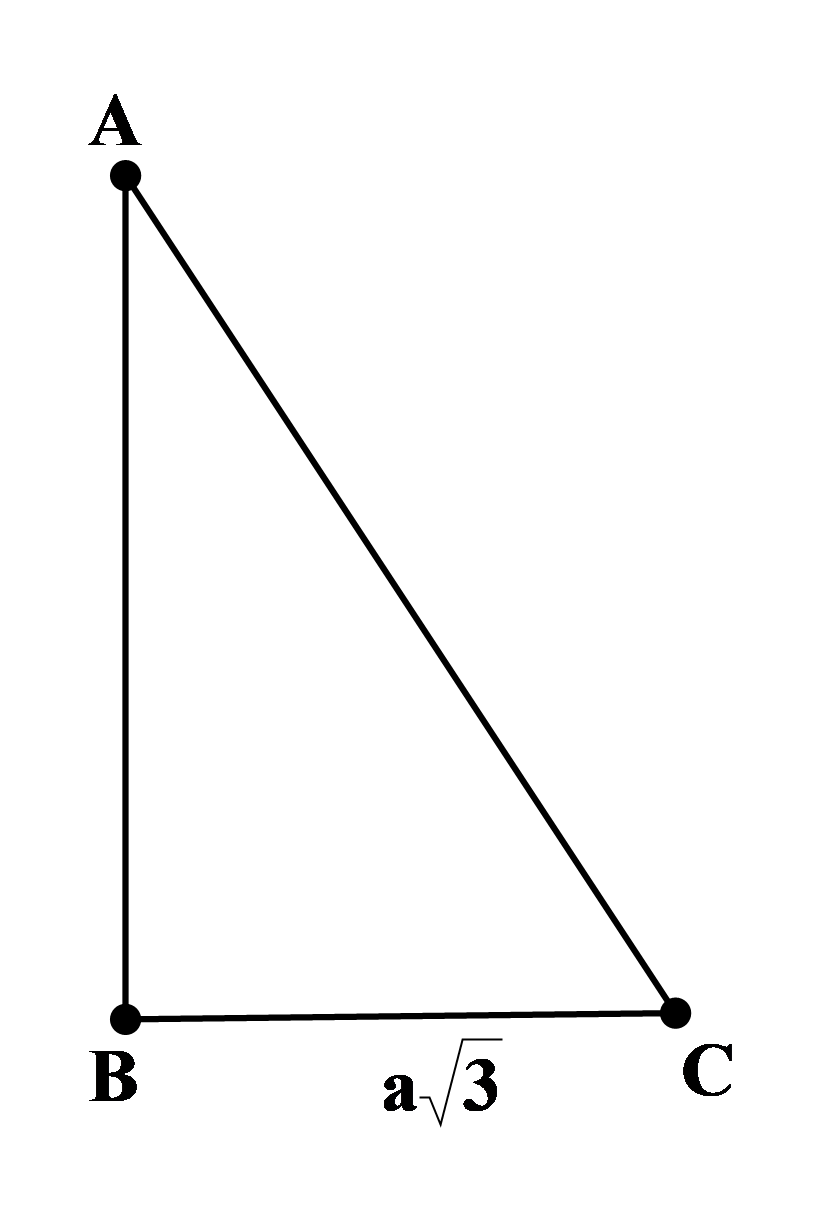
    Ta có:

    \overrightarrow{AC}.\overrightarrow{CB} = \left| \overrightarrow{AC} \right|\left| \overrightarrow{CB} \right|.cos\left( \overrightarrow{AC},\overrightarrow{CB} \right)

    = \left| \overrightarrow{AC} \right|\left| \overrightarrow{CB} \right|.cos\left( 180{^\circ} - \widehat{C} \right)

    = - \left| \overrightarrow{AC} \right|\left| \overrightarrow{CB} \right|.cos\widehat{C} = - \left| \overrightarrow{AC} \right|\left| \overrightarrow{CB} \right|.\frac{BC}{AC} = - BC^{2} = - 3a^{2}.

  • Câu 7: Nhận biết
    Tìm mệnh đề sai

    Gọi G là trọng tâm tam giác đều ABC có cạnh bằng a. Mệnh đề nào sau đây là sai?

    Hướng dẫn:

    Dựa vào đáp án, ta có nhận xét sau:

    Xác định được góc \left( \overrightarrow{AB},\overrightarrow{AC} \right) là góc \widehat{A} nên \left( \overrightarrow{AB},\overrightarrow{AC} \right) = 60^{0}

    Do đó \overrightarrow{AB}.\overrightarrow{AC} =AB.AC.\cos\left( \overrightarrow{AB},\overrightarrow{AC} \right) =a.a.\cos60^{0} = \frac{a^{2}}{2} suy ra \overrightarrow{AB}.\overrightarrow{AC} = \frac{1}{2}a^{2} đúng.

    Xác định được góc \left( \overrightarrow{AC},\overrightarrow{CB} \right) là góc ngoài của góc \widehat{C} nên \left( \overrightarrow{AC},\overrightarrow{CB} \right) = 120^{0}

    Do đó \overrightarrow{AC}.\overrightarrow{CB} =AC.CB.\cos\left( \overrightarrow{AC},\overrightarrow{CB} \right) =a.a.\cos120^{0} = - \frac{a^{2}}{2} suy ra \overrightarrow{AC}.\overrightarrow{CB} = - \frac{1}{2}a^{2} đúng.

    Xác định được góc \left( \overrightarrow{GA},\overrightarrow{GB} \right) là góc \widehat{AGB} nên \left( \overrightarrow{GA},\overrightarrow{GB} \right) = 120^{0}

    Do đó \overrightarrow{GA}.\overrightarrow{GB} =GA.GB.\cos\left( \overrightarrow{GA},\overrightarrow{GB} \right) =\frac{a}{\sqrt{3}}.\frac{a}{\sqrt{3}}.\cos120^{0} = -\frac{a^{2}}{6} suy ra \overrightarrow{GA}.\overrightarrow{GB} = \frac{a^{2}}{6} sai.

    Xác định được góc \left( \overrightarrow{AB},\overrightarrow{AG} \right) là góc \widehat{GAB} nên \left( \overrightarrow{AB},\overrightarrow{AG} \right) = 30^{0}

    Do đó \overrightarrow{AB}.\overrightarrow{AG} =AB.AG.\cos\left( \overrightarrow{AB},\overrightarrow{AG} \right) =a.\frac{a}{\sqrt{3}}.\cos30^{0} = \frac{a^{2}}{2} suy ra\overrightarrow{AB}.\overrightarrow{AG} = \frac{1}{2}a^{2} đúng.

  • Câu 8: Nhận biết
    Chọn kết luận đúng

    Biết \overrightarrow{a}, \overrightarrow{b} \neq \overrightarrow{0} và \overrightarrow{a}.\overrightarrow{b} = - \left| \overrightarrow{a} \right|.\left| \overrightarrow{b} \right|. Câu nào sau đây đúng?

    Hướng dẫn:

    Ta có:

    \overrightarrow{a}.\overrightarrow{b} = - \left|\overrightarrow{a} \right|.\left| \overrightarrow{b} \right|

    \Leftrightarrow \left| \overrightarrow{a} \right|.\left|\overrightarrow{b} \right|\cos\left(\overrightarrow{a},\overrightarrow{b} \right) = - \left|\overrightarrow{a} \right|.\left| \overrightarrow{b}\right|

    \Leftrightarrow \cos\left( \overrightarrow{a},\overrightarrow{b} \right) = - 1 nên \overrightarrow{a}và \overrightarrow{b} ngược hướng

  • Câu 9: Nhận biết
    Chọn đáp án đúng

    Cho tam giác ABC vuông tại C có AC = 9, BC = 5. Tính \overrightarrow{AB}.\overrightarrow{AC}?

    Hướng dẫn:

    Ta có:

    \overrightarrow{AB}.\overrightarrow{AC} = \left(\overrightarrow{AC} + \overrightarrow{CB} \right).\overrightarrow{AC}=\overrightarrow{AC}.\overrightarrow{AC} +\overrightarrow{CB}.\overrightarrow{AC} =\overrightarrow{AC}.\overrightarrow{AC} = 81.

  • Câu 10: Nhận biết
    Chọn đáp án đúng

    Cho tam giác ABC có BC = a,\ \ CA = b,\ AB = c. Tính P = \left( \overrightarrow{AB} + \overrightarrow{AC} \right).\overrightarrow{BC}?

    Hướng dẫn:

    Ta có :

    P = \left( \overrightarrow{AB} + \overrightarrow{AC} \right).\overrightarrow{BC} = \left( \overrightarrow{AB} + \overrightarrow{AC} \right).\left( \overrightarrow{BA} + \overrightarrow{AC} \right)

    = \left( \overrightarrow{AC} + \overrightarrow{AB} \right).\left( \overrightarrow{AC} - \overrightarrow{AB} \right)

    = {\overrightarrow{AC}}^{2} - {\overrightarrow{AB}}^{2} = AC^{2} - AB^{2} = b^{2} - c^{2}

  • Câu 11: Nhận biết
    Tính tích vô hướng giữa hai vectơ

    Cho tam giác đều ABC cạnh bằng a và H là trung điểm BC. Tính \overrightarrow{AH}.\overrightarrow{CA}

    Hướng dẫn:

    Ta có:

    \overrightarrow{AH}.\overrightarrow{CA} =AH.CA.\cos\left( \overrightarrow{AH},\overrightarrow{CA} \right)=\frac{a\sqrt{3}}{2}.a.\cos150^{o} = - \frac{3a^{2}}{4}.

  • Câu 12: Nhận biết
    Tính tích vô hướng của hai vectơ

    Cho tam giác đều ABC có cạnh bằng a. Tính tích vô hướng \overrightarrow{AB}.\overrightarrow{AC}.

    Hướng dẫn:

    Xác định được góc \left( \overrightarrow{AB},\overrightarrow{AC} \right) là góc \widehat{A} nên \left( \overrightarrow{AB},\overrightarrow{AC} \right) = 60^{0}.

    Do đó \overrightarrow{AB}.\overrightarrow{AC} =AB.AC.\cos\left( \overrightarrow{AB},\overrightarrow{AC} \right) =a.a.\cos60^{0} = \frac{a^{2}}{2}.

  • Câu 13: Nhận biết
    Chọn câu đúng

    Cho tam giác ABC. Lấy điểm M trên BC sao cho \overrightarrow{AB}.\overrightarrow{AM} - \overrightarrow{AC}.\overrightarrow{AM} = 0. Câu nào sau đây đúng

    Hướng dẫn:

    Ta có:

    \overrightarrow{AB}.\overrightarrow{AM} -\overrightarrow{AC}.\overrightarrow{AM} = 0

    \Leftrightarrow\overrightarrow{AM}\left( \overrightarrow{AB} - \overrightarrow{AC}\right) = 0\Leftrightarrow \overrightarrow{AM}.\overrightarrow{CB} =0 nên AM\bot BC.

  • Câu 14: Nhận biết
    Tính giá trị biểu thức P

    Cho hình vuông ABCD cạnh a. Tính P = \overrightarrow{AC}.\left( \overrightarrow{CD} + \overrightarrow{CA} \right)?

    Hướng dẫn:

    Từ giả thiết suy ra AC = a\sqrt{2}

    Ta có:

    P = \overrightarrow{AC}.\left(\overrightarrow{CD} + \overrightarrow{CA} \right)=\overrightarrow{AC}.\overrightarrow{CD} +\overrightarrow{AC}.\overrightarrow{CA}= -\overrightarrow{CA}.\overrightarrow{CD} -{\overrightarrow{AC}}^{2}

    = - CA.CD\cos\left(\overrightarrow{CA},\overrightarrow{CD} \right) - AC^{2}= -a\sqrt{2}.a.\cos45^{0} - \left( a\sqrt{2} \right)^{2} = -3a^{2}

  • Câu 15: Nhận biết
    Xác định tích vô hướng

    Cho 2 vectơ đơn vị \overrightarrow{a} và \overrightarrow{b} thỏa \left| \overrightarrow{a} + \overrightarrow{b} \right| = 2. Hãy xác định \left( 3\overrightarrow{a} - 4\overrightarrow{b} \right)\left( 2\overrightarrow{a} + 5\overrightarrow{b} \right)?

    Hướng dẫn:

    Ta có:

    \left| \overrightarrow{a} \right| = \left| \overrightarrow{b} \right| = 1, \left| \overrightarrow{a} + \overrightarrow{b} \right| = 2

    \Leftrightarrow \left( \overrightarrow{a} + \overrightarrow{b} \right)^{2} = 4 \Leftrightarrow \overrightarrow{a}.\overrightarrow{b} = 1

    \left( 3\overrightarrow{a} - 4\overrightarrow{b} \right)\left( 2\overrightarrow{a} + 5\overrightarrow{b} \right) = 6{\overrightarrow{a}}^{2} - 20{\overrightarrow{b}}^{2} + 7\overrightarrow{a}.\overrightarrow{b} = - 7.

  • Câu 16: Nhận biết
    Chọn phương án đúng

    Cho ba điểm A,B,C thỏa AB = 2cm,BC = 3cm,CA = 5cm. Tính \overrightarrow{CA}.\overrightarrow{CB}?

    Hướng dẫn:

    Ta có: AB + BC = CA \Rightarrow Ba điểm A,\ \ B,\ \ C thẳng hàng và B nằm giữa A,\ \ C.

    Khi đó

    \overrightarrow{CA}.\overrightarrow{CB} =CA.CB.\cos\left( \overrightarrow{CA},\overrightarrow{CB} \right) =3.5.\cos0^{0} = 15

    Cách khác.

    Ta có:

    AB^{2} = {\overrightarrow{AB}}^{2} = \left( \overrightarrow{CB} - \overrightarrow{CA} \right)^{2} = CB^{2} - 2\overrightarrow{CB}\overrightarrow{CA} + CA^{2}

    \rightarrow\overrightarrow{CB}.\overrightarrow{CA} = \frac{1}{2}\left( CB^{2} +CA^{2} - AB^{2} \right)= \frac{1}{2}\left( 3^{2} + 5^{2} - 2^{2}\right) = 15.

  • Câu 17: Nhận biết
    Chọn mệnh đề đúng

    Cho \overrightarrow{a} và \overrightarrow{b} là hai vectơ cùng hướng và đều khác vectơ \overrightarrow{0}. Mệnh đề nào sau đây đúng?

    Hướng dẫn:

    Do \overrightarrow{a} và \overrightarrow{b} là hai vectơ cùng hướng nên \left( \overrightarrow{a},\overrightarrow{b} \right) = 0^{0} \rightarrow \cos\left( \overrightarrow{a},\overrightarrow{b} \right) = 1.

    Vậy \overrightarrow{a}.\overrightarrow{b} = \left| \overrightarrow{a} \right|.\left| \overrightarrow{b} \right|.

  • Câu 18: Nhận biết
    Chọn đáp án đúng

    Cho tứ giác lồi ABCD có AD = 6cm. Đặt \overrightarrow{v} = \overrightarrow{AB} - \overrightarrow{DC} - \overrightarrow{CB}. Tính \overrightarrow{v}.\overrightarrow{AD} ?

    Hướng dẫn:

    Ta có:

    \overrightarrow{v} = \overrightarrow{AB}- \overrightarrow{DC} - \overrightarrow{CB}= \overrightarrow{AB} +\overrightarrow{CD} + \overrightarrow{BC} = \overrightarrow{AD}

    Suy ra \overrightarrow{v}.\overrightarrow{AD} = AD^{2} = 36cm^{2}.

  • Câu 19: Nhận biết
    Chọn đáp án đúng

    Cho tam giác đều ABC có cạnh bằng a. Tính tích vô hướng \overrightarrow{AB}.\overrightarrow{BC}.

    Hướng dẫn:

    Xác định được góc \left( \overrightarrow{AB},\overrightarrow{BC} \right) là góc ngoài của góc \widehat{B} nên \left( \overrightarrow{AB},\overrightarrow{BC} \right) = 120^{0}

    Do đó \overrightarrow{AB}.\overrightarrow{BC} =AB.BC.\cos\left( \overrightarrow{AB},\overrightarrow{BC} \right) =a.a.\cos120^{0} = - \frac{a^{2}}{2}

  • Câu 20: Nhận biết
    Tìm khẳng định sai

    Cho tam giác ABC vuông cân tại A, AB = 1. Khẳng định nào sau đây sai.

    Hướng dẫn:

    Hình vẽ minh họa:

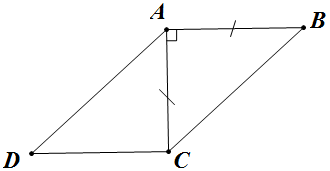
    Gọi D là đỉnh thứ \overrightarrow{IB} = ( - 1;b + 2) của hình bình hành ABCD.

    Khi đó :

    \overrightarrow{AB}.\overrightarrow{BC} =\overrightarrow{AB}.\overrightarrow{AD} = AB.AD.\cos\widehat{BAD}

    =1.\sqrt{2}.\left( - \frac{\sqrt{2}}{2} \right) = - 1.

    Suy ra \overrightarrow{AB}.\overrightarrow{CB} = 1.

  • Câu 21: Nhận biết
    Tính độ dài MN

    Nếu hai điểm M, N thỏa mãn \overrightarrow{MN}.\ \overrightarrow{NM} = - 4 thì độ dài đoạn thẳng MN bằng bao nhiêu?

    Hướng dẫn:

    Ta có:

    \overrightarrow{MN}.\overrightarrow{NM} = \overrightarrow{MN}. (- \overrightarrow{MN})= -MN^{2} = - 4 \Rightarrow MN = 2

  • Câu 22: Nhận biết
    Chọn đáp án đúng

    Cho tam giác ABC vuông tại A có AC = 12\ \ cm. M là trung điểm AC. Tính \overrightarrow{BM}.\overrightarrow{CA}?

    Hướng dẫn:

    Ta có:

    \overrightarrow{BM}.\overrightarrow{CA} = \left( \overrightarrow{BA} + \overrightarrow{AM} \right).\overrightarrow{CA}

    = \overrightarrow{BA}.\overrightarrow{CA} + \overrightarrow{AM}.\overrightarrow{CA} = \overrightarrow{AM}.\overrightarrow{CA} = - 72cm^{2}

  • Câu 23: Nhận biết
    Xác định tích vô hướng giữa hai vectơ

    Cho tam giác ABC vuông tại A và có AB =c,\ AC = b. Tính \overrightarrow{BA}.\overrightarrow{BC}.

    Hướng dẫn:

    Ta có:

    \overrightarrow{BA}.\overrightarrow{BC}= BA.BC.\cos\left( \overrightarrow{BA},\overrightarrow{BC} \right) =BA.BC.\cos\widehat{B}

    = c.\sqrt{b^{2} + c^{2}}.\frac{c}{\sqrt{b^{2} + c^{2}}} = c^{2}

    Cách khác.

    Tam giác ABC vuông tại A suy ra AB\bot AC \Rightarrow \overrightarrow{AB}.\overrightarrow{AC} = 0

    Ta có:

    \overrightarrow{BA}.\overrightarrow{BC} =\overrightarrow{BA}.\left( \overrightarrow{BA} + \overrightarrow{AC}\right)= {\overrightarrow{BA}}^{2} +\overrightarrow{BA}.\overrightarrow{AC} = AB^{2} = c^{2}

  • Câu 24: Nhận biết
    Chọn câu đúng

    Cho tam giác ABC có đường cao BH (H ở trên cạnh AC). Câu nào sau đây đúng?

    Hướng dẫn:

    Ta có:

    \overrightarrow{BA}.\overrightarrow{CA} = \left( \overrightarrow{BH} + \overrightarrow{HA} \right).\overrightarrow{CA}

    = \overrightarrow{BH}.\overrightarrow{CA} + \overrightarrow{HA}.\overrightarrow{CA} = \overrightarrow{HA}.\overrightarrow{CA} = AH.AC nên chọn \overrightarrow{BA}.\overrightarrow{CA} = AH.AC.

    = \overrightarrow{BH}.\overrightarrow{CA} + \overrightarrow{HA}.\overrightarrow{CA} = \overrightarrow{HA}.\overrightarrow{CA} = AH.AC

0/24
24 câu:
Kiểm tra Kiểm tra lại Bỏ qua Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Kết quả làm bài:
  • Nhận biết (100%):
    2/3
  • Thời gian làm bài: 00:00:00
  • Số câu làm đúng: 0
  • Số câu làm sai: 0
  • Điểm số: 0
  • Điểm thưởng: 0
Làm lại
Bạn còn 1 lượt làm bài tập miễn phí. Hãy mua tài khoản VnDoc PRO để học không giới hạn nhé! Bạn đã HẾT lượt làm bài tập miễn phí! Hãy mua tài khoản VnDoc PRO để làm Trắc nghiệm không giới hạn và tải tài liệu nhanh nhé! Mua ngay
1
4 Bài viết đã được lưu
Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!
Số điện thoại này đã được xác thực!
Bạn có thể dùng Sđt này đăng nhập tại đây!
Lỗi gửi SMS, liên hệ Admin
Sắp xếp theo
Xóa Đăng nhập để Gửi
Tìm bài trong mục này
🖼️

Chuyên đề Toán 10
Xem thêm