Cho ba điểm phân biệt. Khi đó:
Điều kiện cần và đủ để thẳng hàng là
cùng phương với
Trong chuyên đề Vectơ Toán 10, khái niệm hai vectơ cùng phương là phần kiến thức quan trọng giúp học sinh hiểu rõ mối quan hệ giữa phương, hướng và độ dài của vectơ. Việc nắm vững đặc điểm và dấu hiệu nhận biết hai vectơ cùng phương không chỉ giúp giải tốt các bài tập hình học mà còn là nền tảng cho các phần tọa độ vectơ và phương trình đường thẳng ở lớp 11 – 12.
Bài viết này tổng hợp bộ câu hỏi trắc nghiệm Toán 10 về hai vectơ cùng phương, kèm đáp án chi tiết và lời giải cụ thể, giúp bạn tự kiểm tra kiến thức, rèn luyện kỹ năng tư duy hình học và củng cố phần Vectơ Toán 10 một cách hiệu quả.
Cho ba điểm phân biệt. Khi đó:
Điều kiện cần và đủ để thẳng hàng là
cùng phương với
Mệnh đề nào sau đây đúng?
Ta có vectơ cùng phương với mọi vectơ.
Vậy mệnh đề đúng là: “Có duy nhất một vectơ cùng phương với mọi vectơ”.
Mệnh đề nào sau đây sai?
Vì có thể xảy ra trường hợp
Khẳng định nào sau đây đúng?
Hai vectơ cùng phương với 1 vectơ thứ ba khác thì cùng phương.
Cho hai vectơ không cùng phương và
. Khẳng định nào sau đây đúng?
Vì vectơ cùng phương với mọi vectơ. Nên có một vectơ cùng phương với cả hai vectơ
và
, đó là vectơ
.
Cho lục giác đều tâm
. Số các vectơ khác vectơ không, cùng phương với
có điểm đầu và điểm cuối là các đỉnh của lục giác là:
Hình vẽ minh họa:
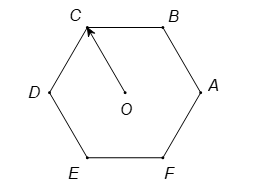
Đó là các vectơ: .
Cho ba điểm thẳng hàng, trong đó điểm
nằm giữa hai điểm
và
. Khi đó các cặp vecto nào sau đây cùng hướng?
Ta có: và
là hai vectơ cùng hướng.
Cho điểm
,
,
không thẳng hàng,
là điểm bất kỳ. Mệnh đề nào sau đây đúng?
Ta có điểm
,
,
không thẳng hàng,
là điểm bất kỳ.
Suy ra không cùng phương
.
Gọi lần lượt là trung điểm của các cạnh
của tam giác đều
. Hỏi cặp vectơ nào sau đây cùng hướng?
Cặp vectơ nào sau đây cùng hướng là: và
Gọi là trung điểm của đoạn
. Hãy chọn khẳng định đúng trong các khẳng định sau:
Ta có là trung điểm của đoạn
và
cùng hướng.
Khẳng định nào sau đây đúng?
Theo định nghĩa: Hai vectơ và
được gọi là bằng nhau, kí hiệu
, nếu chúng cùng hướng và cùng độ dài.
Mệnh đề nào sau đây đúng:
Hai vectơ cùng phương với một vectơ thứ ba khác thì cùng phương.
Phát biểu nào sau đây đúng?
A. sai do hai vectơ không bằng nhau thì có thể hai vecto ngược hướng nhưng độ dài vẫn bằng nhau.
B. sai do một trong hai vectơ là vectơ không.
C. đúng do hai vectơ bằng nhau thì hai vectơ cùng hướng.
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây: