Cho 4 điểm bất kì . Đẳng thức nào sau đây đúng?
Theo quy tắc 3 điểm ta có: .
Trong chương trình Toán 10, phần các phép toán trên vectơ, đặc biệt là hiệu của hai vectơ, đóng vai trò quan trọng giúp học sinh hiểu sâu hơn về bản chất và ứng dụng của vectơ trong hình học phẳng. Bài viết này tổng hợp bộ câu hỏi trắc nghiệm Toán 10 về hiệu của hai vectơ – mức độ nhận biết, giúp bạn vừa ôn luyện lý thuyết, vừa kiểm tra khả năng vận dụng công thức. Các câu hỏi được biên soạn bám sát chương trình học, có đáp án và lời giải chi tiết, hỗ trợ hiệu quả trong quá trình ôn tập chuyên đề Các phép toán vectơ Toán 10.
Cho 4 điểm bất kì . Đẳng thức nào sau đây đúng?
Theo quy tắc 3 điểm ta có: .
Cho hai điểm phân biệt . Điều kiện để điểm
là trung điểm của đoạn thẳng
là:
Vì và
chiều nên
.
Cho ,
đối nhau. Mệnh đề dưới đây sai là:
Ta có: đối nhau nên chúng có cùng độ dài, ngược hướng và có tổng bằng
.
Chọn khẳng định sai:
Ta có: .
Cho hình chữ nhật , gọi
là giao điểm của
và
, phát biểu nào là đúng?
Hình vẽ minh họa:

Ta có: là vectơ đối của
,
là vectơ đối của
Vậy: .
Cho phân biệt, mệnh đề dưới đây đúng là:
Ta có: .
Cho hình bình hành tâm
. Khi đó
Hình vẽ minh họa
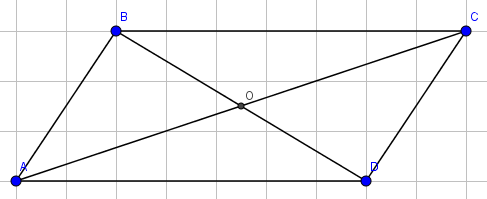
Ta có: .
Cho 4 điểm bất kỳ . Đẳng thức nào sau đây là đúng:
Ta có: (quy tắc 3 điểm).
Gọi là trung điểm của đoạn thẳng
. Đẳng thức nào sau đây là đúng?
Hình vẽ minh họa:
![]()
Ta có: .
Cho tam giác , khẳng định nào sau là đúng?
Ta có: (quy tắc 3 điểm).
Cho hình bình hành có tâm
. Khẳng định nào sau đây là đúng:
Ta có: .
Cho ba điểm phân biệt . Đẳng thức nào sau đây là đúng?
Ta có: (Quy tắc 3 điểm).
Chỉ ra vectơ tổng trong các vectơ sau:
Ta có: .
Chọn đẳng thức đúng:
Ta có: (quy tắc 3 điểm).
Cho hình bình hành với
là giao điểm của 2 đường chéo. Khẳng định nào sau đây là khẳng định sai?
Ta có: không cùng phương và độ lớn nên
.
Cho ba điểm phân biệt. Đẳng thức nào sau đây là đẳng thức sai?
Ta có: .
Cho hình bình hành. Đẳng thức nào sau đây sai?
Ta có:
.
Cho hình bình hành,với giao điểm hai đường chéo là
. Khi đó:
Ta có: .
Cho ba vectơ đều khác vectơ – không. Trong đó hai vectơ
cùng hướng, hai vectơ
đối nhau. Khẳng định nào sau đây đúng?
Hình vẽ minh họa
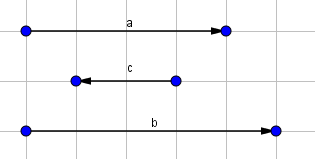
Khẳng định đúng là: “Hai vectơ ngược hướng”.
Cho hình bình hành có tâm
. Khẳng định nào sau đây là sai:
Hình vẽ minh họa:
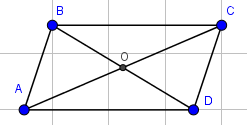
Ta có: .
Cho các điểm phân biệt. Đẳng thức nào sau đây đúng?
Ta có: (qui tắc 3 điểm).
Điều kiện nào sau đây không phải là điều kiện cần và đủ để là trọng tâm của tam giác
, với
là trung điểm của
.
Điều kiện cần và đủ để là trọng tâm của tam giác
là
nên đáp án cần tìm là
.
Cho tam giác có
lần lượt là trung điểm của
. Khi đó, các vectơ đối của vectơ
là:
Hình vẽ minh họa:
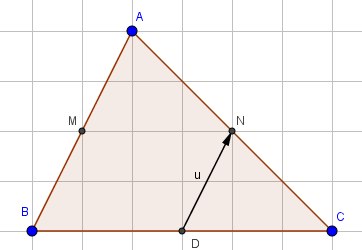
Nhìn hình ta thấy vectơ đối của vectơ là:
.
Chọn kết quả sai:
Ta có: .
Cho 3 điểm . Đẳng thức nào sau đây đúng.
Ta có: (quy tắc 3 điểm).
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây: