Bất phương trình bậc hai một ẩn - Cách giải và bài tập có đáp án
Bất phương trình bậc hai lớp 10 Có đáp án
Trong chương trình Toán 10, bất phương trình bậc hai một ẩn là một chuyên đề trọng tâm, thường xuyên xuất hiện trong các đề kiểm tra và đề thi THPT Quốc gia. Việc nắm vững cách giải bất phương trình bậc hai, hiểu rõ điều kiện xác định, bảng xét dấu và quy tắc dấu tam thức bậc hai sẽ giúp học sinh xử lý nhanh, chính xác mọi dạng bài.
Trong bài viết này, chúng ta sẽ cùng tìm hiểu lý thuyết cơ bản, phương pháp giải chi tiết và bài tập minh họa có đáp án, giúp bạn củng cố kiến thức và rèn luyện kỹ năng giải toán hiệu quả.
A. Định nghĩa và cách giải bất phương trình bậc hai một ẩn
Bất phương trình bậc hai (ẩn 
\(x\)) là bất phương trình có một trong các dạng:
\(f(x) > 0,\ \ f(x) < 0,\ \ f(x)
\geq 0,\ \ f(x) \leq 0\), trong đó \(f(x)\) là một tam thức bậc hai.
Cách giải. Để giải bất phương trình bậc hai, ta áp dụng định lí về dấu của tam thức bậc hai.
B. Ví dụ minh họa giải bất phương trình bậc hai một ẩn
Ví dụ 1: Cho hàm số bậc hai \(y =
f(x)\)có đồ thị hình vẽ. Dựa vào đồ thị hãy viết tập nghiệm của các bất phương trình \(f(x) > 0;\ \ f(x)
\geq 0;\ \ f(x) < 0;\ \ f(x) \leq 0.\)
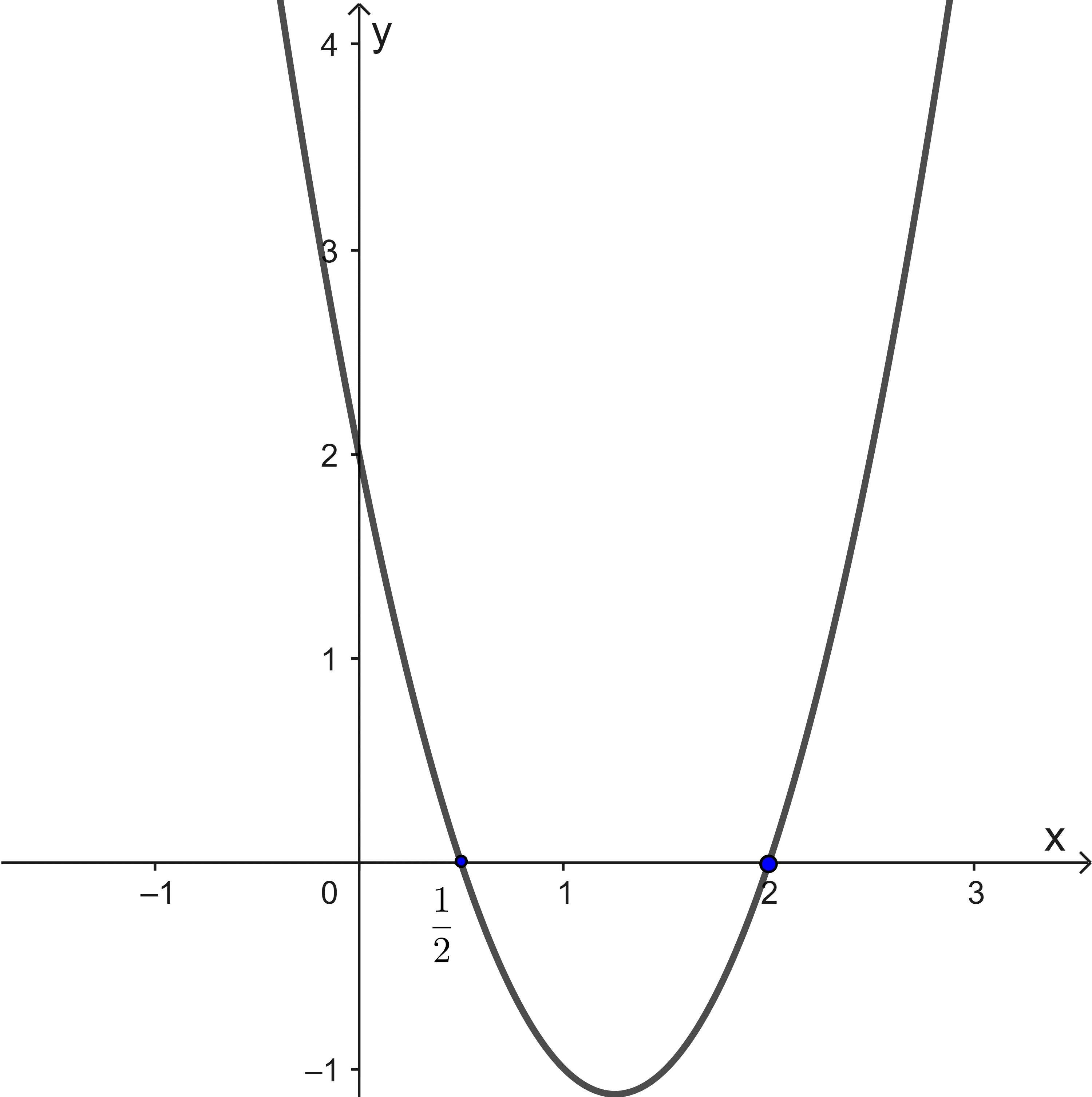
Hướng dẫn giải
Dựa vào đồ thị ta có:
\(f(x) > 0 \Leftrightarrow x \in \left(
- \infty;\frac{1}{2} \right) \cup (2; + \infty)\)
\(f(x) \geq 0 \Leftrightarrow x \in \left(- \infty; \frac{1}{2} \right\rbrack \cup \lbrack 2; +\infty)\)
\(f(x) < 0 \Leftrightarrow x \in \left(
\frac{1}{2};2 \right)\)
\(f(x) \leq 0 \Leftrightarrow x \notin
\left\lbrack \frac{1}{2};2 \right\rbrack\)
Ví dụ 2: Giải các bất phương trình bậc hai:
a) \(x^{2} - 1 \geq 0\) b) \(x^{2} - 2x - 1 < 0\)
Hướng dẫn giải
a) Dễ thấy \(f(x) = x^{2} - 1\) có \(\Delta' = 1 > 0,a = 1 > 0\) và có hai nghiệm phân biệt \(x_{1} = - 1;\
x_{2} = 1\).
Do đó ta có bảng xét dấu \(f(x)\):
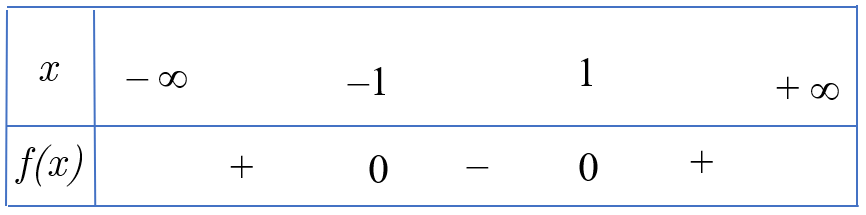
Nên bất phương trình \(x^{2} - 1 \geq
0\) có tập nghiệm là \(S = ( - \infty;
- 1) \cup (1; + \infty)\).
b) Dễ thấy \(g(x) = x^{2} - 2x - 1\) có \(\Delta' = 2 > 0,a = 1 >
0\) và có hai nghiệm phân biệt \(x_{1}
= 1 - \sqrt{2};\) \(x_{2} = 1 +
\sqrt{2}\).
Do đó ta có bảng xét dấu \(g(x)\):
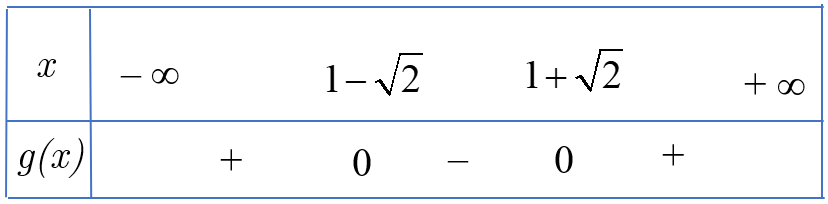
Nên bất phương trình \(x^{2} - 2x - 1 <
0\) có tập nghiệm là \(S = \left( 1 -
\sqrt{2};1 + \sqrt{2} \right)\).
Ví dụ 3: Giải bất phương trình sau: \(-
3x^{2} + 2x + 1 < 0\).
Hướng dẫn giải
Tam thức \(f(x) = - 3x^{2} + 2x +
1\) có \(a = - 3 < 0\) và có hai nghiệm \(x_{1} = - \frac{1}{3};\) \(x_{2} = 1\)
(\(f(x)\) cùng dấu với hệ số \(a\)).
Suy ra \(- 3x^{2} + 2x + 1 < 0
\Leftrightarrow x < - \frac{1}{3}\) hoặc \(x > 1\)
Vậy tập nghiệm của bất phương trình: \(S =
\left( - \infty; - \frac{1}{3} \right) \cup (1; + \infty)\).
Ví dụ 4: Tìm tập xác định của hàm số: \(y =
\sqrt{x^{2} - 2x + 5}\).
Hướng dẫn giải
Điều kiện: \(x^{2} - 2x + 5 \geq
0\)
Xét tam thức vế trái có \(\Delta' = - 4
< 0\) và \(a = 1 > 0\) nên \(x^{2} - 2x + 5 > 0,\forall x\mathbb{\in
R}\).
Vậy tập xác định của hàm số \(D\mathbb{=
R}\).
Ví dụ 5: Tìm các giá trị của \(m\) để biểu thức \(f(x) = - x^{2} - 2x -
m\) luôn âm?
Hướng dẫn giải
Ta có: \(f(x) < 0,\forall x
\Leftrightarrow \left\{ \begin{matrix}
a = - 1 < 0 \\
\Delta' = 1 - 4m < 0
\end{matrix} \right.\ \Leftrightarrow m > \frac{1}{4}\)
Vậy với \(- \frac{1}{4} < m <
0\) thì biểu thức \(f(x)\) luôn âm.
C. Bài tập tự rèn luyện giải bất phương trình bậc hai một ẩn có lời giải
Bài tập 1: Cho hàm số bậc hai \(y =
f(x)\)có đồ thị hình vẽ. Dựa vào đồ thị hãy viết tập nghiệm của các bất phương trình \(f(x) > 0;\ \ f(x)
\geq 0;\ \ f(x) < 0;\ \ f(x) \leq 0.\)
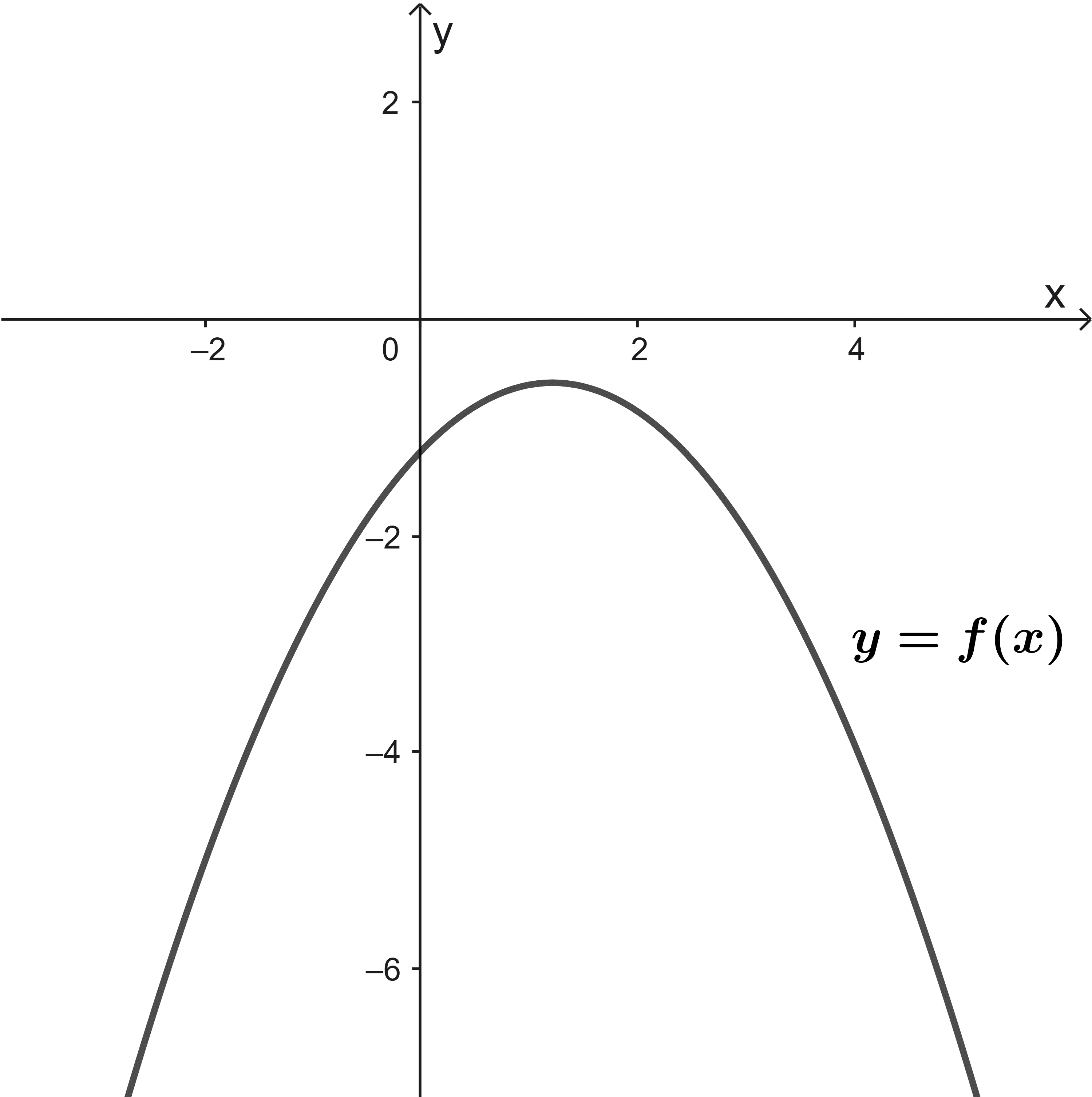
Bài tập 2: Giải các bất phương trình bậc hai:
a) \(- 3x^{2} + 12x + 1 \leq 0\) b) \(5x^{2} + x + 1 \geq 0\)
Bài tập 3: Giải bất phương trình sau \(-
36x^{2} + 12x - 1 \geq 0\).
Bài tập 4: Giải bất phương trình \(\left(
x^{2} - x \right)^{2} + 3\left( x^{2} - x \right) + 2 \geq
0\).
Tài liệu quá dài để hiển thị hết — hãy nhấn Tải về để xem trọn bộ!
-------------------------------------------------
Qua chuyên đề bất phương trình bậc hai một ẩn, học sinh không chỉ nắm vững bản chất của dạng toán mà còn thành thạo các phương pháp giải nhanh, chính xác và dễ hiểu. Việc luyện tập thường xuyên với hệ thống bài tập có đáp án chi tiết sẽ giúp bạn tự tin hơn trong các bài kiểm tra và kỳ thi quan trọng.
