Cách giải hệ bất phương trình bậc nhất hai ẩn
Cách xác định miền nghiệm của hệ bất phương trình bậc nhất hai ẩn
Trong chương trình Toán 10, việc học và rèn luyện với hệ bất phương trình bậc nhất hai ẩn đóng vai trò rất quan trọng. Đây là dạng toán giúp học sinh hiểu rõ mối quan hệ giữa các bất phương trình, đồng thời rèn luyện kỹ năng biểu diễn miền nghiệm trên mặt phẳng tọa độ. Nắm vững cách giải hệ bất phương trình bậc nhất hai ẩn sẽ giúp bạn xử lý nhanh các bài tập từ cơ bản đến nâng cao, đồng thời tạo nền tảng vững chắc để tiếp cận những chuyên đề phức tạp hơn trong đại số. Bài viết này không chỉ cung cấp phương pháp giải chi tiết mà còn kèm theo ví dụ minh họa và hệ bất phương trình bậc nhất hai ẩn Toán 10 có đáp án, giúp bạn dễ hiểu và áp dụng hiệu quả.
A. Hệ bất phương trình bậc nhất hai ẩn
Hệ bất phương trình bậc nhất hai ẩn là một hệ gồm một hai hay nhiều bất phương trình bậc nhất hai ẩn.
\(\left\{ \begin{matrix}
a_{1}x + b_{1}y \leq c_{1} \\
a_{2}x + b_{2}y \leq c_{2} \\
...
\end{matrix} \right.\)
Trong đó \(a_{i};b_{i};c_{i}\) là các số đã cho \(x;y\) là ẩn.
Cặp số \(\left( x_{0};y_{0}
\right)\) là nghiệm của hệ bất phương trình bậc nhất hai ẩn khi \(\left( x_{0};y_{0} \right)\) đồng thời là nghiệm của tất cả các bất phương trình trong hệ đó.
B. Các bước giải hệ bất phương trình bậc nhất hai ẩn
Bước 1: Mỗi bất phương trình có thể viết lại thành
\(ax + by \leq c\) hoặc \(ax + by \geq c\)
Bước 2. Với mỗi bất phương trình \(ax + by
\leq c\) ta vẽ đường thẳng biên
\(ax + by = c\)
Đường thẳng này chia mặt phẳng thành hai nửa mặt phẳng.
Bước 3. Lấy một điểm thử (thường chọn \(O(0;0)\) nếu không nằm trên đường thẳng) thay vào bất phương trình.
Nếu điểm đó thỏa mãn thì nửa mặt phẳng chứa điểm đó là miền nghiệm.
Nếu không thì miền nghiệm là nửa mặt phẳng còn lại.
Bước 4. Tìm giao miền nghiệm
Miền nghiệm của hệ là phần giao của tất cả miền nghiệm các bất phương trình trong hệ.
C. Bài tập ví dụ minh họa giải hệ bất phương trình bậc nhất hai ẩn
Ví dụ 1. Một gia đình cần ít nhất \(900\) đơn vị protein và \(400\) đơn vị lipit trong thức ăn mỗi ngày. Mỗi kiogam thịt bò chứa \(800\) đơn vị protein và \(200\) đơn vị lipit. Mỗi kilogam thịt lợn chứa \(600\)đơn vị protein và \(400\) đơn vị lipit. Biết rằng gia đình này chỉ mua nhiều nhất \(1,6\) kg thịt bò và \(1,1\) kg thịt lợn. Giá tiền một kg thịt bò là \(160\) nghìn đồng, một kg thịt lợn là \(110\) nghìn đồng. Gọi \(\ x\),\(y\) lần lượt là số kg thịt bò và thịt lợn mà gia đình đó cần mua. Tìm \(\
x\),\(y\) để tổng số tiền họ phải trả là ít nhất mà vẫn đảm bảo lượng protein và lipit trong thức ăn?
Hướng dẫn giải
Theo bài ra ta có số tiền gia đình cần trả là \(160x + 110y\) với \(\ x\),\(y\) thỏa mãn: \(\left\{ \begin{matrix}
0 \leq x \leq 1,6 \\
0 \leq y \leq 1,1
\end{matrix} \right.\).
Số đơn vị protein gia đình có là \(0,8x +
0,6y \geq 0,9 \Leftrightarrow 8x + 6y \geq 9\left( d_{1}
\right)\).
Số đơn vị lipit gia đình có là\(0,2x + 0,4y
\geq 0,4 \Leftrightarrow \ x + 2y \geq 2\) \(\left( d_{2} \right)\).
Bài toán trở thành: Tìm \(x,y\) thỏa mãn hệ bất phương trình \(\left\{
\begin{matrix}
0 \leq x \leq 1,6 \\
0 \leq y \leq 1,1 \\
8x + 6y \geq 9 \\
x + 2y \geq 2
\end{matrix} \right.\) sao cho \(T =
160x + 110y\) nhỏ nhất.
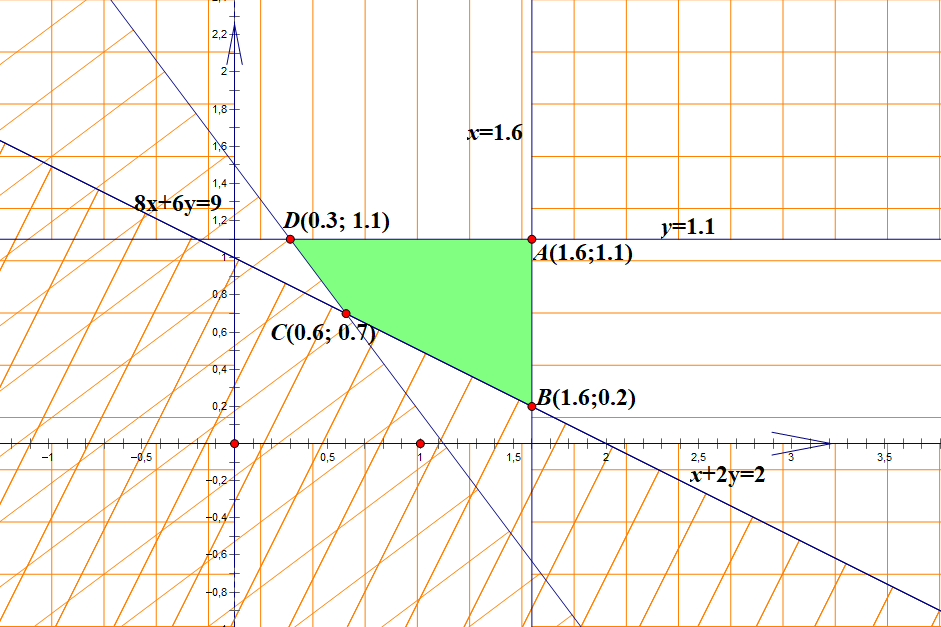
Vẽ hệ trục tọa độ ta tìm được tọa độ các điểm \(A(1,6;\ 1,1)\); \(B(1,6;\ 0,2)\); \(C(0,6;\ 0,7)\); \(D(0,3;\ 1,1)\).
Nhận xét: \(T(A) = 377\) nghìn, \(T(B) = 278\) nghìn, \(T(C) = 173\) nghìn, \(T(D) = 169\) nghìn.
Vậy tổng số tiền họ phải trả là ít nhất mà vẫn đảm bảo lượng protein và lipit trong thức ăn thì \(x = 0,3\) và \(y = 1,1\).
Ví dụ 2. Một học sinh dự định vẽ các tấm thiệp xuân làm bằng tay để bán trong hội chợ Tết. Cần 2 giờ để vẽ tấm thiệp loại nhỏ có giá 10 nghìn đồng và 3 giờ để vẽ tấm thiệp loại lớn có giá 20 nghìn đồng. Học sinh này chỉ có 30 giờ để vẽ và ban tổ chức hội chợ yêu cầu phải vẽ ít nhất 12 tấm. Hãy cho biết bạn ấy phải vẽ bao nhiêu tấm thiệp mỗi loại để có nhiều tiền nhất?
Hướng dẫn giải
Gọi \(x\) là số tấm thiệp nhỏ vẽ được và \(y\) là số tấm thiệp lớn vẽ được
\(\left\{ \begin{matrix}
x + y \geq 12 \\
2x + 3y \leq 30 \\
x \geq 0 \\
y \geq 0
\end{matrix} \right.\)
Biểu diễn miền nghiệm của hệ bất phương trình trên hệ trục Oxy ta có:
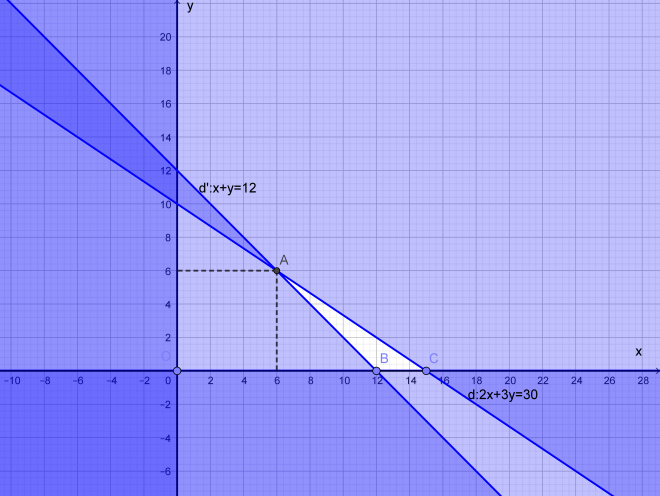
Số tiền kiếm được là \(T = 10x +
20y\) (nghìn đồng)
Tại \(A(6;6)\)thì \(T = 180\)
Tại \(B(12;0)\) thì \(T = 120\)
Tại \(C(15;0)\) thì \(T = 150\)
Vậy bạn ấy phải vẽ 6 tấm thiệp mỗi loại để có nhiều tiền nhất.
Ví dụ 3. Một học sinh tham gia hoạt động gây quỹ bằng cách xếp giấy Origami để bán. Bạn cần 2 giờ để xếp được một mô hình cỡ nhỏ, bán với giá 90 nghìn đồng và 3 giờ để xếp được một mô hình cỡ trung, bán với giá 120 nghìn đồng. Học sinh này đặt ra kế hoạch là thời gian hoàn thành không quá 15 giờ và phải xếp được ít nhất 6 mô hình. Hãy cho biết học sinh đó có thể thu được số tiền gây quỹ cao nhất là bao nhiêu?
Hướng dẫn giải
Gọi x, y lần lượt là số mô hình cỡ nhỏ , cỡ trung mà bạn học sinh cần xếp.
Ta có hệ bất phương trình: \(\left\{ \begin{matrix}
2x + 3y \leq 15 \\
\ \ \ x + \ \ \ y \geq 6 \\
\ \ \ \ \ \ \ \ \ \ \ \ x \geq 0 \\
\ \ \ \ \ \ \ \ \ \ \ \ y \geq 0
\end{matrix} \right.\)
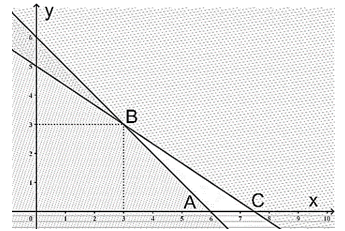
Gọi số tiền thu được là \(F(x;y) = 90x +
120y\) (đơn vị: nghìn đồng )
Tại \(A(6;0) \Rightarrow F =
540\)
Tại \(B(3;3) \Rightarrow F =
630\)
Tại \(C(7,5\ ;0)\) ( loại)
Ta thấy:
điểm \(M(7;0)\) thuộc miền tam giác ABC mà \(F(7;0) = 630\)
điểm \(N(6;1)\) thuộc miền tam giác ABC mà \(F(6;1) = 660\)
điểm \(E(5;1)\) thuộc miền tam giác ABC mà \(F(5;1) = 570\)
điểm \(F(4;2)\) thuộc miền tam giác ABC mà \(F(4;2) = 600\)
Vậy học sinh đó thu được số tiền gây quỹ cao nhất là 660 nghìn đồng.
C. Bài tập tự rèn luyện giải hệ bất phương trình bậc nhất hai ẩn
Bài 1. Một xưởng sản xuất hai loại sản phẩm như sau: Mỗi kg sản phẩm loại I cần 2 kg nguyên liệu và 30 giờ, mức lời 40 nghìn; Mỗi kg sản phẩm loại II cần 4 kg nguyên liệu và 15 giờ, mức lời 30 nghìn. Xưởng có 200 kg nguyên liệu và 1200 giờ làm việc. Nên sản xuất mỗi loại sản phẩm bao nhiêu để có mức lời cao nhất?
Bài 2. Một hộ nông dân định trồng dứa và củ đậu trên diện tích \(8ha\). Trên diện tích mỗi \(ha\), nếu
trồng dứa thì cần 20 công và thu 3 triệu đồng, nếu trồng củ đậu thì cần 30 công và thu 4 triệu đồng. Hỏi cần trồng mỗi loại cây trên với diện tích là bao nhiêu \(ha\) để thu được nhiều tiền nhất, biết rằng tổng số công không quá 180.
A. 1 \(ha\) dứa và 7 \(ha\) củ đậu. B. 8 \(ha\) củ đậu.
C. 2 \(ha\) dứa và 6 \(ha\) củ đậu. D. 6 \(ha\) dứa và 2 \(ha\) củ đậu.
Bài 3. Biết rằng miền nghiệm của hệ bất phương trình \(\left\{ \begin{matrix}
x + 2y - 100 \leq 0 \\
2x + y - 80 \leq 0 \\
x \geq 0 \\
y \geq 0
\end{matrix} \right.\) là một đa giác được cho như hình vẽ bên dưới (phần không gạch sọc). Giá trị lớn nhất của biểu thức \(F(x,y) = 2x + 3y\) với \((x;y)\) thuộc miền nghiệm của hệ bất phương trình trên là bao nhiêu?
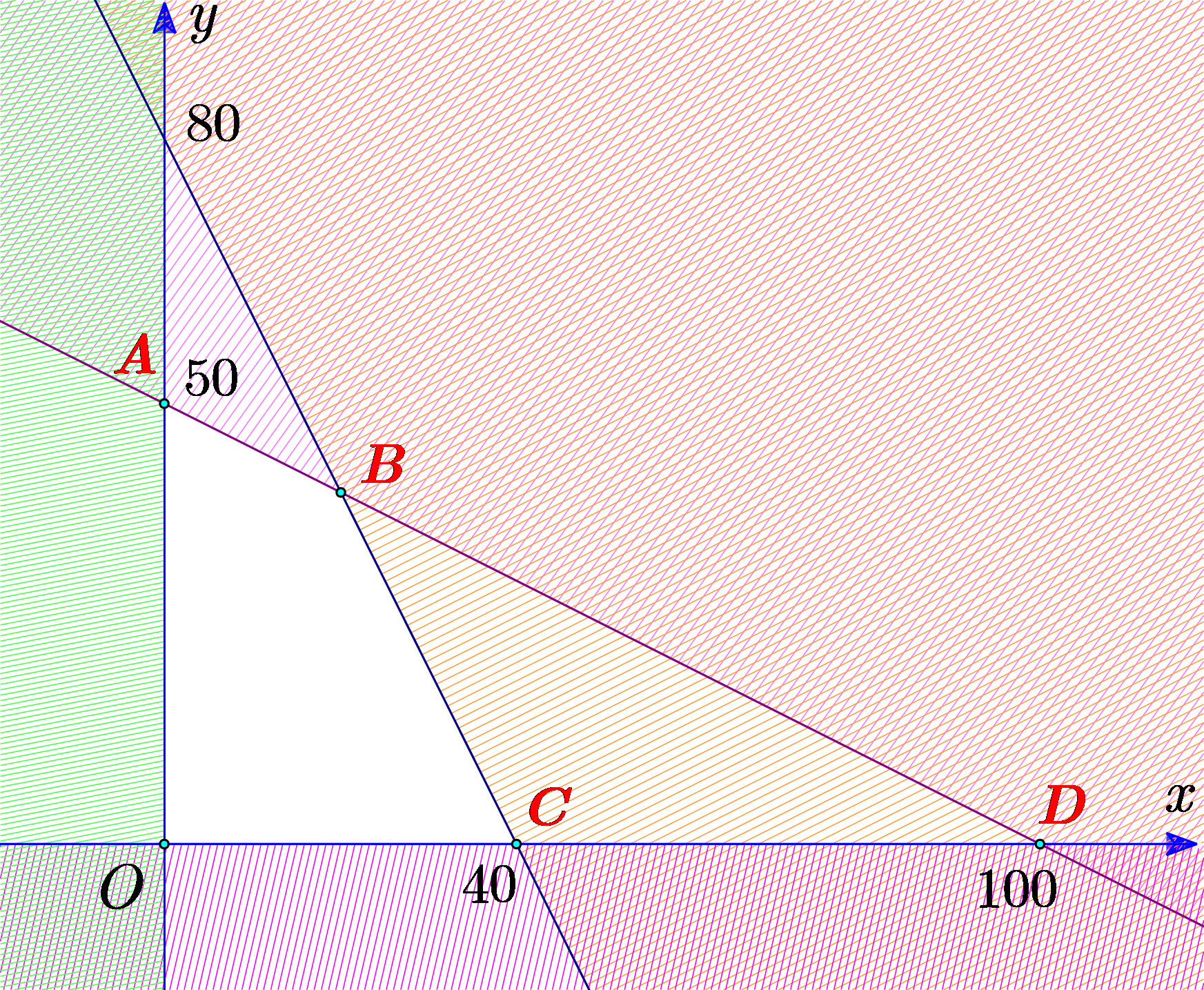
A. 150. B. 80. C. 230. D. 160.
Toàn bộ nội dung đã sẵn sàng! Nhấn Tải về để tải đầy đủ tài liệu!
---------------------------------------------------------
Qua bài viết này, bạn đã nắm được cách giải hệ bất phương trình bậc nhất hai ẩn một cách khoa học và chi tiết. Khi luyện tập thường xuyên với các bài tập có lời giải chi tiết, bạn sẽ dễ dàng nhận biết được dạng toán, xác định miền nghiệm và trình bày lời giải chặt chẽ, logic. Đây là kỹ năng nền tảng, giúp bạn không chỉ học tốt hệ bất phương trình bậc nhất hai ẩn Toán 10 mà còn vận dụng thành thạo trong các đề kiểm tra, đề thi học kỳ và kỳ thi quan trọng. Hãy tiếp tục luyện tập với nhiều dạng toán khác nhau để củng cố kiến thức, phát triển tư duy toán học và chinh phục điểm số cao trong môn Toán.
