Cách xét dấu của tam thức bậc hai
Dấu của tam thức bậc hai Toán 10 - Có đáp án
Bạn đang tìm hiểu về cách xét dấu của tam thức bậc hai để giải nhanh các bài tập bất phương trình Toán 10? Đây là một kỹ năng quan trọng giúp bạn xử lý hiệu quả những bài toán liên quan đến parabol, tìm khoảng nghiệm và đánh giá dấu của biểu thức bậc hai. Trong bài viết này, chúng tôi sẽ hướng dẫn bạn từng bước cách xét dấu của tam thức bậc hai rõ ràng, dễ hiểu, kèm theo bài tập bất phương trình Toán 10 có đáp án để bạn rèn luyện và nâng cao kỹ năng giải toán.
A. Công thức xét dấu của tam thức bậc hai
Định nghĩa: Tam thức bậc hai đối với x là biểu thức có dạng ![]() \(f(x) = ax^{2} + bx + c\), trong đó a, b, c là các hệ số;
\(f(x) = ax^{2} + bx + c\), trong đó a, b, c là các hệ số; ![]() \(a \neq
0\).
\(a \neq
0\).
Định lí: Cho ![]() \(f(x) = ax^{2} + bx + c;(a
\neq 0);\Delta = b^{2} - 4ac\).
\(f(x) = ax^{2} + bx + c;(a
\neq 0);\Delta = b^{2} - 4ac\).
Nếu ![]() \(\Delta < 0\) thì
\(\Delta < 0\) thì ![]() \(f(x)\) luôn cùng dấu với a, tức là
\(f(x)\) luôn cùng dấu với a, tức là![]() \(\forall x\mathbb{\in R}:af(x) >
0\).
\(\forall x\mathbb{\in R}:af(x) >
0\).

Nếu ![]() \(\Delta = 0\) thì
\(\Delta = 0\) thì ![]() \(f(x)\) luôn cùng dấu với a trừ khi
\(f(x)\) luôn cùng dấu với a trừ khi ![]() \(x = - \frac{b}{a}\), tức là
\(x = - \frac{b}{a}\), tức là ![]() \(\forall x \neq - \frac{b}{a}:af(x) > 0\) (hay
\(\forall x \neq - \frac{b}{a}:af(x) > 0\) (hay ![]() \(\forall x\mathbb{\in R}:af(x) \geq
0\), đẳng thức xảy ra khi và chỉ khi
\(\forall x\mathbb{\in R}:af(x) \geq
0\), đẳng thức xảy ra khi và chỉ khi ![]() \(x = - \frac{b}{2a}\)).
\(x = - \frac{b}{2a}\)).
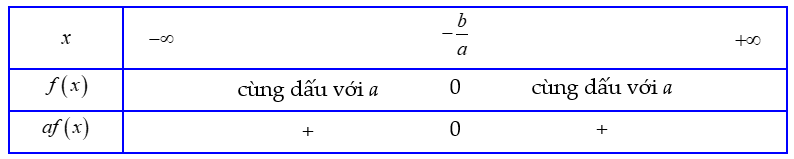
Nếu ![]() \(\Delta > 0\) thì
\(\Delta > 0\) thì ![]() \(f(x)\) cùng dấu với a khi
\(f(x)\) cùng dấu với a khi ![]() \(x < x_{1}\) hoặc
\(x < x_{1}\) hoặc ![]() \(x > x_{2}\), trái dấu với a khi
\(x > x_{2}\), trái dấu với a khi ![]() \(x_{1} < x < x_{2}\), trong đó
\(x_{1} < x < x_{2}\), trong đó ![]() \(x_{1};x_{2};\left( x_{1} < x_{2}
\right)\) là hai nghiệm của
\(x_{1};x_{2};\left( x_{1} < x_{2}
\right)\) là hai nghiệm của ![]() \(f(x)\), tức là:
\(f(x)\), tức là:
![]() \(af(x) < 0 \Leftrightarrow x_{1} <
x < x_{2}\)
\(af(x) < 0 \Leftrightarrow x_{1} <
x < x_{2}\)
![]() \(af(x) > 0 \Leftrightarrow
\left\lbrack \begin{matrix}
x < x_{1} \\
x > x_{2} \\
\end{matrix} \right.\)
\(af(x) > 0 \Leftrightarrow
\left\lbrack \begin{matrix}
x < x_{1} \\
x > x_{2} \\
\end{matrix} \right.\)

Lưu ý:
+ Ta có thể dùng  \(\Delta' =
b'^{2} - ac\) thay cho Δ.
\(\Delta' =
b'^{2} - ac\) thay cho Δ.
+ Một số kết quả quan trọng:
 \(ax^{2} + bx + c > 0;\forall x
\Leftrightarrow \left\{ \begin{matrix}
a > 0 \\
\Delta < 0 \\
\end{matrix} \right.\);
\(ax^{2} + bx + c > 0;\forall x
\Leftrightarrow \left\{ \begin{matrix}
a > 0 \\
\Delta < 0 \\
\end{matrix} \right.\); \(ax^{2} + bx + c \geq 0;\forall x
\Leftrightarrow \left\{ \begin{matrix}
a > 0 \\
\Delta \leq 0 \\
\end{matrix} \right.\);
\(ax^{2} + bx + c \geq 0;\forall x
\Leftrightarrow \left\{ \begin{matrix}
a > 0 \\
\Delta \leq 0 \\
\end{matrix} \right.\); \(ax^{2} + bx + c < 0;\forall x
\Leftrightarrow \left\{ \begin{matrix}
a < 0 \\
\Delta < 0 \\
\end{matrix} \right.\);
\(ax^{2} + bx + c < 0;\forall x
\Leftrightarrow \left\{ \begin{matrix}
a < 0 \\
\Delta < 0 \\
\end{matrix} \right.\); \(ax^{2} + bx + c \leq 0;\forall x
\Leftrightarrow \left\{ \begin{matrix}
a < 0 \\
\Delta \leq 0 \\
\end{matrix} \right.\).
\(ax^{2} + bx + c \leq 0;\forall x
\Leftrightarrow \left\{ \begin{matrix}
a < 0 \\
\Delta \leq 0 \\
\end{matrix} \right.\).
B. Bài tập ví dụ minh họa xét dấu của tam thức bậc hai
Ví dụ 1: Xét dấu các tam thức bậc hai sau:
a) ![]() \(f(x) = x^{2} + x + 1\) b)
\(f(x) = x^{2} + x + 1\) b) ![]() \(g(x) = - x^{2} + 3x - 2\)
\(g(x) = - x^{2} + 3x - 2\)
Lời giải
a) Ta có: ![]() \(\Delta = 1 - 4.1.1 = - 3 <
0\) mà
\(\Delta = 1 - 4.1.1 = - 3 <
0\) mà ![]() \(a = 1 > 0\). Vậy
\(a = 1 > 0\). Vậy ![]() \(f(x) > 0;\forall x\mathbb{\in
R}\).
\(f(x) > 0;\forall x\mathbb{\in
R}\).
b) Ta có: ![]() \(g(x)\) có 2 nghiệm là:
\(g(x)\) có 2 nghiệm là: ![]() \(x_{1} = 1;x_{2} = - 1\) và
\(x_{1} = 1;x_{2} = - 1\) và ![]() \(a = 1 < 0\).
\(a = 1 < 0\).
Bảng xét dấu ![]() \(g(x)\):
\(g(x)\):

Ví dụ 2: Gọi S là tập hợp tất cả các giá trị của tham số m để hàm số ![]() \(y = f(x) = \sqrt{mx^{2}
- 2(2m - 1)x + 4m}\) xác định với mọi
\(y = f(x) = \sqrt{mx^{2}
- 2(2m - 1)x + 4m}\) xác định với mọi ![]() \(x\mathbb{\in R}\). Hỏi S chứa khoảng nào trong các khoảng sau?
\(x\mathbb{\in R}\). Hỏi S chứa khoảng nào trong các khoảng sau?
A. ![]() \(( - 2;0)\) B.
\(( - 2;0)\) B. ![]() \((0;2)\) C.
\((0;2)\) C. ![]() \((2;4)\) D.
\((2;4)\) D. ![]() \((0;4)\)
\((0;4)\)
Lời giải
Hàm số xác định ![]() \(\forall x\mathbb{\in
R}\)
\(\forall x\mathbb{\in
R}\)
![]() \(\Leftrightarrow mx^{2} - 2(2m - 1)x + 4m
\geq 0;\forall x\mathbb{\in R}\)
\(\Leftrightarrow mx^{2} - 2(2m - 1)x + 4m
\geq 0;\forall x\mathbb{\in R}\)
Trướng hợp 1:  \(\left\{ \begin{matrix}
a = 0 \\
b = 0 \\
c \geq 0 \\
\end{matrix} \right.\ \Leftrightarrow \left\{ \begin{matrix}
m = 0 \\
- 2(2m - 1) = 0 \\
4m \geq 0 \\
\end{matrix} \right.\) (Hệ vô nghiệm).
\(\left\{ \begin{matrix}
a = 0 \\
b = 0 \\
c \geq 0 \\
\end{matrix} \right.\ \Leftrightarrow \left\{ \begin{matrix}
m = 0 \\
- 2(2m - 1) = 0 \\
4m \geq 0 \\
\end{matrix} \right.\) (Hệ vô nghiệm).
Trường hợp 2:  \(\left\{ \begin{matrix}
a > 0 \\
\Delta' \leq 0 \\
\end{matrix} \right.\ \Leftrightarrow \left\{ \begin{matrix}
m > 0 \\
- 4m + 1 \leq 0 \\
\end{matrix} \right.\ \Leftrightarrow \left\{ \begin{matrix}
m > 0 \\
m \geq \frac{1}{4} \\
\end{matrix} \right.\ \Leftrightarrow m \geq \frac{1}{4}\).
\(\left\{ \begin{matrix}
a > 0 \\
\Delta' \leq 0 \\
\end{matrix} \right.\ \Leftrightarrow \left\{ \begin{matrix}
m > 0 \\
- 4m + 1 \leq 0 \\
\end{matrix} \right.\ \Leftrightarrow \left\{ \begin{matrix}
m > 0 \\
m \geq \frac{1}{4} \\
\end{matrix} \right.\ \Leftrightarrow m \geq \frac{1}{4}\).
Vậy ![]() \(S = \left\lbrack \frac{1}{4}; +
\infty \right)\). Do đó S chứa khoảng
\(S = \left\lbrack \frac{1}{4}; +
\infty \right)\). Do đó S chứa khoảng![]() \((2;4)\).
\((2;4)\).
---------------------------------------------------------------
Hy vọng qua bài viết này, bạn đã nắm vững cách xét dấu của tam thức bậc hai và áp dụng thành thạo vào các dạng bài bất phương trình Toán 10 có đáp án. Khi luyện tập thường xuyên, bạn sẽ không chỉ giải nhanh hơn mà còn tự tin trong mọi kỳ kiểm tra, thi học kỳ hay thi tốt nghiệp.
Hãy lưu lại bài viết này để ôn tập bất cứ khi nào, chia sẻ cho bạn bè để cùng nhau tiến bộ, và khám phá thêm nhiều chuyên đề Toán 10 khác như phương trình bậc hai, bất phương trình chứa căn, hay bất phương trình chứa ẩn ở mẫu. Chúc bạn học tốt, chinh phục mọi bài toán và đạt điểm cao nhất!









