Tìm m để bất phương trình có đúng một nghiệm
Điều kiện để bất phương trình có đúng một nghiệm
Trong chương trình Toán 10, chuyên đề bất phương trình là nền tảng quan trọng giúp học sinh rèn luyện kỹ năng tư duy logic và giải quyết các bài toán liên quan đến nghiệm. Một trong những dạng bài thường gặp là Tìm m để bất phương trình có đúng một nghiệm — dạng toán giúp học sinh hiểu sâu hơn về mối quan hệ giữa tham số m, nghiệm của tam thức bậc hai và tính chất dấu của biểu thức bậc hai.
Bài viết này sẽ tổng hợp kiến thức lý thuyết, phương pháp giải chi tiết, cùng bài tập minh họa có đáp án, giúp bạn dễ dàng nhận diện và chinh phục dạng toán này một cách hiệu quả.
Ví dụ 1. Với điều kiện nào của m thì phương trình 
\(mx^{2} - 2(m - 1)x + m - 2 = 0\) có đúng 1 nghiệm thuộc khoảng (-1; 2)?
A. \(- 2 \leq m \leq 1\). B. \(\left\lbrack \begin{matrix}
m < - 1 \\
m > 1
\end{matrix} \right.\). C. \(m <
\frac{4}{3}\). D. \(0 < m <
\frac{4}{3}\).
Hướng dẫn giải
Chọn A
Khi \(m = 0\), phương trình \(\Leftrightarrow x = 1 \in ( - 1;\ 2)\).
Ta có \(m = 0\) (thỏa mãn yêu cầu).(*)
Khi \(m \neq 0\), phương trình luôn có hai nghiệm \(x = 1;\ x = \frac{m -
2}{m}\).
Phương trình có đúng 1 nghiệm thuộc khoảng (-1; 2)
\(\Leftrightarrow \left\lbrack \begin{matrix}
\frac{m - 2}{m} \leq - 1 \\
\frac{m - 2}{m} \geq 2
\end{matrix} \right.\ \Leftrightarrow \left\lbrack \begin{matrix}
\frac{2m - 2}{m} \leq 0 \\
\frac{- m - 2}{m} \geq 0
\end{matrix} \right.\ \Leftrightarrow \left\lbrack \begin{matrix}
0 < m \leq 1 \\
- 2 \leq m < 0
\end{matrix} \right.\).
Kết hợp (*) ta có \(- 2 \leq m \leq
1\).
Ví dụ 2. Bảng xét dấu nào sau đây là của tam thức \(f(x) = - \ x^{2} + \ 6x - 9\)?
A. 
. B. 
.
C. 
. D. 
.
Hướng dẫn giải
Chọn C
Tam thức có 1 nghiệm \(x = 3\) và hệ số \(a = - 1 < 0\)
Vậy đáp án cần tìm là C
Ví dụ 3. Để phương trình: \(|x + 3|(x - 2)
+ m - 1 = 0\)có đúng một nghiệm, các giá trị của tham số \(m\)là:
A. \(m < 1\) hoặc \(m > \frac{29}{4}\). B. \(m\ < - \ \frac{21}{4}\) hoặc \(m > 1\).
C. \(m < - 1\) hoặc \(m > \frac{21}{4}\). D. \(m < - \ \frac{29}{4}\) hoặc \(m > 1\).
Hướng dẫn giải
Chọn A
Ta có \(|x + 3|(x - 2) + m - 1 = 0
\Leftrightarrow m = 1 - |x + 3|(x - 2)\)
Xét hàm số \(y = 1 - |x + 3|(x -
2)\)
Ta có \(y = \left\{ \begin{matrix}
- x^{2} - x + 7\ \ \ \ khi\ \ \ \ x \geq - 3 \\
x^{2} + x - 5\ \ \ \ \ \ \ \ khi\ \ \ \ \ x < - 3
\end{matrix} \right.\)
Bảng biến thiên của \(y = 1 - |x + 3|(x -
2)\)
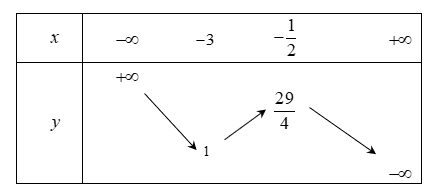
Dựa vào bảng trên phương trình có đúng 1 nghiệm khi và chỉ khi\(\left\lbrack \begin{matrix}
m < 1 \\
m > \frac{29}{4}
\end{matrix} \right.\)
Ví dụ 4. Để phương trình sau có nghiệm duy nhất: \(\left| 2x^{2} - 3x - 2 \right| = 5a - 8x -
x^{2}\). Giá trị của tham số \(a\) là:
A. \(a = 15\). B. \(a = - 12\). C. \(a = - \frac{56}{79}\). D. \(a = - \frac{49}{60}\).
Hướng dẫn giải
Chọn A
Xét phương trình: \(\left| 2x^{2} - 3x - 2
\right| = 5a - 8x - x^{2}(1)\)
Khi đó:
\(5a = f(x) = \left( 2x^{2} - 3x - 2
\right) + 8x + x^{2}\) khi \(2x^{2} -
3x - 2 \geq 0\)
Hay \(3x^{2} + 5x - 2\) khi \(2x^{2} - 3x - 2 \geq 0\)
Và \(5a = f(x) - 2x^{2} + 3x + 2 + 8x +
x^{2}\) khi \(\ 2x^{2} - 3x - 2 <
0\)
Hay \(- x^{2} + 11x + 2\) khi \(\ 2x^{2} - 3x - 2 < 0\)
Bảng biến thiên:
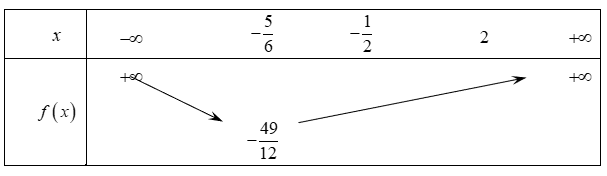
Dựa vào bảng biến thiên ta có: phương trình (1) có nghiệp duy nhất \(5a = - \frac{49}{12} \Leftrightarrow a =
\frac{- 49}{60}\).
--------------------------------------------------------------------
Dạng toán Tìm m để bất phương trình có đúng một nghiệm không chỉ giúp củng cố kiến thức về tam thức bậc hai mà còn rèn luyện khả năng phân tích điều kiện của nghiệm trong từng trường hợp cụ thể. Qua hệ thống bài tập có đáp án chi tiết, học sinh lớp 10 có thể tự đánh giá năng lực và nâng cao kỹ năng giải bất phương trình.
Hãy thường xuyên luyện tập theo chuyên đề Bất phương trình Toán 10 để đạt kết quả cao trong các kỳ kiểm tra và ôn thi THPT Quốc gia môn Toán.
