Tìm m để hệ bất phương trình có nghiệm
Giải hệ bất phương trình một ẩn chứa tham số m
Trong chương trình Toán 10, chuyên đề bất phương trình luôn là một nội dung trọng tâm, gắn liền với nhiều dạng toán từ cơ bản đến nâng cao. Một trong những dạng bài thường gặp trong các kỳ kiểm tra và đề thi học sinh giỏi là tìm m để hệ bất phương trình có nghiệm. Đây là dạng toán tham số, yêu cầu học sinh vừa nắm chắc kiến thức về cách giải bất phương trình, vừa biết phân tích điều kiện để hệ có nghiệm. Bài viết này sẽ hướng dẫn chi tiết phương pháp giải kèm ví dụ minh họa và đáp án, giúp bạn rèn luyện kỹ năng làm bài hiệu quả.
A. Cách tìm m để hệ bất phương trình có nghiệm
Để giải bài toán tìm m để hệ bất phương trình có nghiệm ta thực hiện theo các bước như sau:
Bước 1. Viết lại hệ bất phương trình dưới dạng chuẩn: 
\(\left\{ \begin{matrix}
f(x) > 0 \\
g(x) \leq 0 \\
.....
\end{matrix} \right.\).
Bước 2. Tìm tập nghiệm của từng bất phương trình theo tham số m.
Bước 3. Xét giao của các tập nghiệm
Hệ bất phương trình có nghiệm khi và chỉ khi giao của các tập nghiệm khác rỗng.
Bước 4. Rút ra khoảng hoặc miền giá trị của tham số m.
Bước 5. Kết luận
B. Bài tập tìm m để hệ bất phương trình có nghiệm
Ví dụ 1: Hệ bất phương trình \(\left\{\begin{matrix}3(x - 6) < - 3 \\\dfrac{5x + m}{2} > 7\end{matrix} \right.\) (với m là tham số) có nghiệm khi và chỉ khi:
A. \(m \leq - 11\) B. \(m \geq - 11\) C. \(m < - 11\) D. \(m > - 11\)
Hướng dẫn giải
Ta có: \(3\left( {x - 6} \right) < - 3 \Leftrightarrow x - 6 < - 1 \Leftrightarrow x < 5\)
\(\frac{5x + m}{2} > 7 \Leftrightarrow
5x + m > 14 \Leftrightarrow x > \frac{14 - m}{5}\).
Vậy hệ bất phương trình đã cho có nghiệm khi và chỉ khi
\(\frac{14 - m}{5} < 5 \Leftrightarrow
14 - m < 25 \Leftrightarrow m > - 11\).
Ví dụ 2: Cho hệ bất phương trình \(\left\{
\begin{matrix}
mx^{2} - x - 5 \leq 0 \\
(1 - m)x^{2} + 2mx + m + 2 \geq 0
\end{matrix} \right.\) (với m là tham số).
a) Giải hệ bất phương trình khi \(m =
1\)
A. \(S = \left\lbrack \frac{1 -
2\sqrt{21}}{2};\frac{1 + 2\sqrt{21}}{2} \right\rbrack\) B. \(S = \left\lbrack \frac{1 - 3\sqrt{21}}{2};\frac{1
+ 3\sqrt{21}}{2} \right\rbrack\)
C. \(S = \left\lbrack \frac{1 -
4\sqrt{21}}{2};\frac{1 + 4\sqrt{21}}{2} \right\rbrack\) D. \(S = \left\lbrack \frac{1 - \sqrt{21}}{2};\frac{1 +
\sqrt{21}}{2} \right\rbrack\)
b) Tìm m để hệ bất phương trình nghiệm đúng với mọi x
A. \(\frac{- 1 - 2\sqrt{17}}{4} \leq m \leq
- \frac{31}{20}\) B. \(m \leq -
\frac{1}{20}\)
C. \(\frac{- 1 - \sqrt{17}}{4} \leq
m\) D. \(\frac{- 1 - \sqrt{17}}{4} \leq
m \leq - \frac{1}{20}\)
Hướng dẫn giải
a) Khi \(m = 1\) hệ bất phương trình trở thành
\(\left\{ \begin{matrix}x^{2} - x - 5 \leq 0 \\2x + 3 \geq 0\end{matrix} \right.\ \Leftrightarrow \left\{ \begin{matrix}\frac{1 - \sqrt{21}}{2} \leq x \leq \dfrac{1 + \sqrt{21}}{2} \\x \geq - \dfrac{3}{2}\end{matrix} \right.\)
\(\Leftrightarrow \frac{1 - \sqrt{21}}{2}
\leq x \leq \frac{1 + \sqrt{21}}{2}\)
Vậy tập nghiệm hệ bất phương trình là \(S =
\left\lbrack \frac{1 - \sqrt{21}}{2};\frac{1 + \sqrt{21}}{2}
\right\rbrack\)
b) Khi \(m = 0\) hệ bất phương trình trở thành \(\left\{ \begin{matrix}
- x - 5 \leq 0 \\
x^{2} + 2 \geq 0
\end{matrix} \right.\)(vô nghiệm) do đó \(m = 0\) không thỏa mãn yêu cầu bài toán
Khi \(m = 1\) theo câu a ta thấy cũng không thỏa mãn yêu cầu bài toán
Khi \(\left\{ \begin{matrix}
m \neq 0 \\
m \neq 1
\end{matrix} \right.\) ta có hệ bất phương trình nghiệm đúng với mọi x khi và chỉ khi các bất phương trình trong hệ bất phương trình nghiệm đúng với mọi \(x\)
\(\Leftrightarrow \left\{ \begin{matrix}
\left\{ \begin{matrix}
m < 0 \\
\Delta_{1} = 1 + 20m \leq 0
\end{matrix} \right.\ \\
\left\{ \begin{matrix}
1 - m > 0 \\
\Delta'_{2} = m^{2} - (1 - m)(m + 2) \leq 0
\end{matrix} \right.\
\end{matrix} \right.\) \(\Leftrightarrow \left\{ \begin{matrix}m < 0 \\m \leq - \dfrac{1}{20} \\m < 1 \\2m^{2} + m - 2 \leq 0\end{matrix} \right.\)
\(\Leftrightarrow \left\{ \begin{matrix}m < 0 \\m \leq - \dfrac{1}{20} \\m < 1 \\\frac{- 1 - \sqrt{17}}{4} \leq m \leq \dfrac{- 1 + \sqrt{17}}{4}\end{matrix} \right.\) \(\Leftrightarrow \frac{- 1 - \sqrt{17}}{4} \leq m
\leq - \frac{1}{20}\)
Vậy \(\frac{- 1 - \sqrt{17}}{4} \leq m \leq-\frac{1}{20}\) là giá trị cần tìm.
Ví dụ 3: Tìm tất cả các giá trị của tham số \(m\) để hệ sau có nghiệm \(\left\{ \begin{matrix}
x^{2} - 3x + 2 \leq 0 \\
mx^{2} - 2(2m + 1)x + 5m + 3 \geq 0
\end{matrix} \right.\).
A. \(m > - \frac{1}{2}\) B. \(m = - \frac{1}{2}\) C. \(m \geq - \frac{1}{2}\) D. \(m = \varnothing\)
Hướng dẫn giải
Ta có bất phương trình \(x^{2} - 3x + 2
\leq 0 \Leftrightarrow 1 \leq x \leq 2\).
Yêu cầu bài toán tương đương với bất phương trình:
\(mx^{2} - 2(2m + 1)x + 5m + 3 \leq
0\) (1) có nghiệm \(x \in S = \lbrack1;2\rbrack\).
Ta đi giải bài toán phủ định là: tìm \(m\) để bất phương trình (1) vô nghiệm trên \(S\)
Tức là bất phương trình \(f(x) = mx^{2} -
2(2m + 1)x + 5m + 3 < 0\) (2) đúng với mọi \(x \in S\).
• \(m = 0\) ta có (2) \(\Leftrightarrow - 2x + 3 < 0 \Leftrightarrow x
> \frac{3}{2}\) nên (2) không đúng với \(\forall x \in S\)
• \(m \neq 0\) tam thức \(f(x)\) có hệ số \(a = m\), biệt thức \(\Delta' = - m^{2} + m + 1\)
Bảng xét dấu
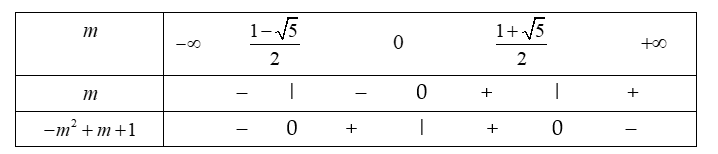
+) \(m \geq \frac{1 + \sqrt{5}}{2}\) ta có: \(\left\{ \begin{matrix}
a > 0 \\
\Delta' \leq 0
\end{matrix} \right.\) nên \(f(x)
\geq 0,\ \forall x\mathbb{\in R}\), suy ra \(m \geq \frac{1 + \sqrt{5}}{2}\) không thỏa mãn
+) \(m \leq \frac{1 - \sqrt{5}}{2}\) ta có: \(\left\{ \begin{matrix}
a < 0 \\
\Delta' \leq 0
\end{matrix} \right.\) nên \(f(x)
\leq 0,\ \forall x\mathbb{\in R}\) và \(f\left( \frac{3 - \sqrt{5}}{2} \right) =
0\), suy ra \(m \leq \frac{1 -
\sqrt{5}}{2}\) thỏa mãn.
+) \(\frac{1 - \sqrt{5}}{2} < m <
0\) ta có: \(a < 0\) và \(f(x)\) có hai nghiệm phân biệt
\(x_{1} = \frac{2m + 1 +
\sqrt{\Delta'}}{m},\ x_{2} = \frac{2m + 1 -
\sqrt{\Delta'}}{m}\) (\(x_{1} <
x_{2}\))
Do đó: \(f(x) < 0 \Leftrightarrow
\left\lbrack \begin{matrix}
x < x_{1} \\
x > x_{2}
\end{matrix} \right.\), suy ra (2) đúng với \(\forall x \in S \Leftrightarrow \left\lbrack
\begin{matrix}
x_{1} > 2 \\
x_{2} < 1
\end{matrix} \right.\) (*)
Ta có \(x_{1} = 2 + \frac{1 +
\sqrt{\Delta'}}{m} < 2\)
\(x_{2} < 1 \Leftrightarrow\sqrt{\Delta'} < m + 1\)\(\Leftrightarrow \left\{ \begin{matrix}\frac{1 - \sqrt{5}}{2} < m < 0 \\\Delta' < m^{2} + 2m + 1\end{matrix} \right.\)
\(\Leftrightarrow \left\{ \begin{gathered}
\frac{{1 - \sqrt 5 }}{2} < m < 0 \hfill \\
2{m^2} + m > 0 \hfill \\
\end{gathered} \right.\)\(\Leftrightarrow \left\{ \begin{gathered}
\frac{{1 - \sqrt 5 }}{2} < m < 0 \hfill \\
\left[ {\begin{array}{*{20}{c}}
{m > 0} \\
{m < - \frac{1}{2}}
\end{array}} \right. \hfill \\
\end{gathered} \right.\)\(\Leftrightarrow \frac{{1 - \sqrt 5 }}{2} < m < - \frac{1}{2}\)
Suy ra (*)\(\Leftrightarrow \frac{1 -
\sqrt{5}}{2} < m < - \frac{1}{2}\)
+) \(0 < m < \frac{1 +
\sqrt{5}}{2}\) ta có: \(a <
0\) và \(f(x)\) có hai nghiệm phân biệt
\(x_{1} = \frac{2m + 1 +
\sqrt{\Delta'}}{m},\ x_{2} = \frac{2m + 1 -
\sqrt{\Delta'}}{m}\) (\(x_{1} >
x_{2}\))
Suy ra \(f(x) < 0 \Leftrightarrow x \in
\left( x_{2};x_{1} \right)\)
Do đó (2) đúng với \(\forall x \in S
\Leftrightarrow \left\{ \begin{matrix}
x_{2} < 1 \\
x_{1} > 2
\end{matrix} \right.\ \Leftrightarrow \left\{ \begin{matrix}
\sqrt{\Delta'} + m + 1 < 0 \\
\sqrt{\Delta'} + 1 > 0
\end{matrix} \right.\)(**)
Vì \(m > 0\) nên (**) vô nghiệm.
Từ đó, ta thấy (2) đúng với \(\forall x \in
S \Leftrightarrow m < - \frac{1}{2}\).
Vậy \(m \geq - \frac{1}{2}\) là những giá trị cần tìm.
----------------------------------------------------
Qua chuyên đề tìm m để hệ bất phương trình có nghiệm, học sinh không chỉ củng cố kỹ năng giải bất phương trình một ẩn, bậc hai hay hệ nhiều bất phương trình mà còn rèn luyện khả năng tư duy logic khi xử lý tham số. Đây là nền tảng quan trọng để tự tin chinh phục các dạng toán khó hơn trong chương trình THPT và các kỳ thi quan trọng. Để đạt kết quả cao, bạn nên luyện tập đa dạng bài tập, tự thử sức với các đề nâng cao, đồng thời tham khảo đáp án chi tiết để đối chiếu và rút kinh nghiệm. Hy vọng tài liệu thuộc chuyên đề Toán 10 Bất phương trình có đáp án này sẽ là trợ thủ đắc lực giúp bạn học tập hiệu quả hơn.
