Ứng dụng thực tế các phép toán Tập hợp Nâng cao
Giải bài toán tập hợp nâng cao theo ví dụ thực tế
Trong chương trình Toán 10, phần tập hợp nâng cao không chỉ giúp học sinh hiểu sâu hơn về lý thuyết mà còn rèn luyện tư duy logic thông qua các phép toán tập hợp như hợp, giao, hiệu, phần bù,... Điều quan trọng hơn là các kiến thức này có ứng dụng thực tế trong việc giải quyết nhiều bài toán trong đời sống, thống kê và khoa học máy tính. Trong bài viết này, chúng ta sẽ cùng tìm hiểu cách vận dụng các phép toán tập hợp nâng cao vào thực tế, đồng thời luyện tập với các bài tập Toán 10 có đáp án chi tiết, giúp học sinh tự tin chinh phục mọi dạng bài liên quan.
Bài tập 1: Trong đột khảo sát nghề, giáo viên chủ nhiệm lớp 10D đưa ra ba nhóm ngành cho học sinh lựa chọn, đó là: Giáo dục, Y tế, Công nghệ thông tin. Học sinh có thể chọn từ một đến ba nhóm ngành nêu trên hoặc không chọn nhóm ngành nào trong ba nhóm ngành trên. Giáo viên chủ nhiệm thống kê theo từng nhóm ngành và được kết quả: có 6 học sinh chọn nhóm ngành Giáo dục, 9 học sinh chọn nhóm ngành Y tế, 10 học sinh chọn nhóm ngành Công nghệ thông tin, 22 học sinh không chọn nhóm ngành nào trong ba nhóm trên. Nếu thống kê số lượng học sinh chọn theo từng hai nhóm ngành được kết quả: có 3 học sinh chọn hai nhóm ngành Giáo dục và Y tế, 2 học sinh chọn hai nhóm ngành Y tế và Công nghệ thông tin, 3 học sinh chọn hai nhóm ngành Giáo dục và Công nghệ thông tin. Hỏi có bao nhiêu học sinh chọn cả ba nhóm ngành nêu trên biết ló́p 10D có 40 học sinh?
Hướng dẫn giải
Gọi 
\(A;B;C\) lần lượt là tập hợp học sinh chọn nhóm ngành Giáo dục, Y tế, Công nghệ thông tin. Khi đó, \(A \cup B \cup C\) là tập hợp các học sinh chọn ít nhất một trong ba nhóm ngành trên.
Do lớp 10D có 40 học sinh và 22 học sinh không chọn nhóm ngành trong ba nhóm ngành trên nên số học sinh chọn ít nhất một trong ba nhóm ngành trên là \(40 - 22 = 18\)
Ta có: \(\left\{ \begin{matrix}
n(A) = 6;n(B) = 9;n(C) = 10 \\
n(A \cup B \cup C) = 18 \\
n(A \cap B) = 3;n(B \cap C) = 2;n(A \cap C) = 3
\end{matrix} \right.\)
Áp dụng công thức:
\(n(A \cup B \cup C) =n(A) + n(B) + n(C) - n(B \cap C)\)\(- n(A \cap B) - n(A \cap C) + n(A \cap B \cap C)\)
Ta có số học sinh chọn cả ba nhóm ngành nêu trên là:
\(n(A \cap B \cap C) = n(A \cup B \cup C)+ n(B \cap C)\)\(+ n(A \cap B) + n(A \cap C) - n(A) - n(B) -n(C)\)
\(= 18 + 3 + 2 + 3 - 6 - 9 - 10 =1\).
Bài tập 2: Một lớp học có 25 học sinh chơi bóng đá, 23 học sinh chơi bóng bàn, 14 học sinh chơi cả bóng đá và bóng bàn, 6 học sinh không chơi môn nào. Tìm số học sinh chỉ chơi một môn thể thao?
Hướng dẫn giải
Gọi \(A\) là tập hợp các học sinh chơi bóng đá, \(B\) là tập hợp các học sinh chơi bóng bàn,
C là tập hợp các học sinh không chơi môn thể thao nào.
Ta có: \(|A|\): là số học sinh chơi bóng đá; \(|B|\): là số học sinh chơi bóng bàn; \(|C|\): là số học sinh không chơi môn thể thao nào.
Khi đó số học sinh chỉ chơi một môn thể thao là:
\(|A| + |B| - 2|A \cap B| = 25 + 23 - 2.14 =
20\)
Bài tập 3: Cho tập hợp \(X = \left\{ 3; -
4;5 \right\}\) có hai tập con \(A\) và \(B\) (số phần tử của tập \(B\) ít hơn số phần tử của tập \(A\)). Có bao nhiêu cặp \((A;B)\) mà \(\left\{ 3; - 4 \right\} \cup (A\backslash B) =
X\)?
Hướng dẫn giải
Do \(\left\{ 3; - 4 \right\} \cup
(A\backslash B) = X\) nên tập hợp \(A\backslash B\) phải chứa phần tử 5.
Từ đó suy ra: \(5 \in A;5 \notin
B\).
Các tập con của \(X\) có phân tử 5 là: \(\left\{ 5 \right\},\left\{ 5;3
\right\},\left\{ 5; - 4 \right\},\left\{ 5;3; - 4 \right\}\).
Do số phân tử của tập B ít hơn số phân tử của tập A nên ta có các trường hợp sau:
+ Nếu \(A = \left\{ 5 \right\}\) thì B là tập con của X không chứa phần tử nào, tức là \(B = \varnothing\).
+ Nếu \(A = \left\{ 5;3 \right\}\) thì B là tập con của X chứa ít hơn hai phân tử và không chứa phân tử 5, tức là \(B = \varnothing;B = \left\{ 3
\right\};B = \left\{ - 4 \right\}\).
+ Nếu \(A = \left\{ 5; - 4
\right\}\) thì B là tập con của X chứa ít hơn hai phần tử và không chứa phân tử 5, tức là \(B =
\varnothing;B = \left\{ 3 \right\};B = \left\{ - 4
\right\}\).
+ Nếu \(A = \left\{ 5;3; - 4
\right\}\) thì B là tập con của X chứa ít hơn ba phân tử và không chứa phân tử 5, tức là \(B = \varnothing;B =
\left\{ 3 \right\};B = \left\{ - 4 \right\};B = \left\{ 3; - 4
\right\}\).
Vậy có \(1 + 3 + 3 + 4 = 11\) cặp \((A;B)\) thỏa mãn yêu câu bài toán.
Bài tập 4: Bạn A thống kê số ngày có mưa, có sương mù ở bản mình trong tháng 3 vào một thời điểm nhất định và được kết quả như sau: 14 ngày có mưa, 15 ngày có sương mù, trong đó 10 ngày có cả mưa và sương mù. Hỏi trong tháng 3 đó có bao nhiêu ngày không có mưa và không có sương mù?
Hướng dẫn giải
Gọi \(A;B\) lần lượt là tập hợp các ngày có mưa, có sương mù. Khi đó, \(A \cap
B\) là tập hợp các ngày có cả mưa và sương mù, \(A \cup B\) là tập hợp các ngày hoặc có mưa hoặc có sương mù.
Ta có: \(n(A) = 14;n(B) = 15;n(A \cap B) =
10\).
Số ngày hoặc có mưa hoặc có sương mù là:
\(n(A \cup B) = n(A) + n(B) - n(A \cap B) =
14 + 15 - 10 = 19\) (ngày).
Tháng 3 có 31 ngày nên số ngày không có mưa và không có sương mù trong tháng 3 đó là: \(31 - 19 = 12\) (ngày).
Bài tập 5: Một 10A có 45 học sinh chuẩn bị cho hội diễn văn nghệ chào mừng ngày nhà giáo Việt Nam 20/11. Trong danh sách đăng kí tham gia tiết mục nhảy và tiết mục hát, có 35 học sinh tham gia tiết mục nhảy, 10 học sinh tham gia cả hai tiết mục. Hỏi có bao nhiêu học sinh trong lớp tham gia tiết mục hát? Biết rằng lớp 10A có 4 bạn vì lí do sức khỏe nên không tham gia tiết mục nào.
Hướng dẫn giải
Kí hiệu \(A\) là tập hợp học sinh tham gia tiết mục nhảy, \(B\) là tập hợp học sinh tham gia tiết mục hát, \(E\) là tập hợp học sinh trong lớp.
Ta có thể biểu diễn ba tập hợp đó bằng biểu đồ Ven như hình bên:
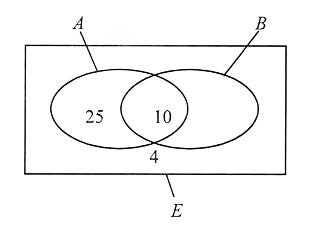
Khi đó, \(A \cap B\) là tập hợp học sinh tham gia cả hai tiết mục. Số phần tử của tập hợp \(A\) là 35, số phần tử của tập hợp \(A \cap B\) là 10, số phần tử của tập hợp \(E\) là 45.
Số học sinh tham gia ít nhất một trong hai tiết mục là \(45 - 4 = 41\) (học sinh).
Số học sinh tham gia tiết mục hát mà không tham gia tiết mục nhảy là \(41 - 35 = 6\) (học sinh).
Số học sinh tham gia tiết mục hát là \(6 +
10 = 16\) (học sinh).
Bài tập 6: Trong đợt khảo sát chất lượng, lớp 10C có \(11\) học sinh đạt điểm giỏi môn Toán, \(8\) học sinh đạt điểm giỏi môn Lý, \(5\) học sinh đạt điểm giỏi cả Toán và Lý, \(4\) học sinh đạt điểm giỏi cả Toán và Hoá, \(2\) học sinh đạt điểm giỏi cả Lý và Hoá, \(1\) học sinh đạt điểm giỏi cả \(3\) môn Toán, Lý, Hoá. Hỏi lớp 10C có bao nhiêu học sinh đạt điểm giỏi môn Hóa, biết trong lớp có 16 học sinh giỏi ít nhất một môn?
Hướng dẫn giải
Biểu đồ Ven:
Gọi \(x\) là số học sinh chỉ giỏi Toán;
\(y\) là số học sinh chỉ giỏi Lý;
\(z\) là số học sinh chỉ giỏi Hóa;
\(a\) là số học sinh chỉ giỏi Toán và Lý;
\(b\) là số học sinh chỉ giỏi Toán và Hóa;
\(c\) là số học sinh chỉ giỏi Hóa và Lý;
\(d\) là số học sinh giỏi cả 3 môn.
Theo đề ra ta có hệ phương trình:
\(\left\{ \begin{matrix}
x + a + b + d = 11\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (1) \\
y + a + c + d = 8\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (2) \\
a + d = 5\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \
\ \ (3) \\
b + d = 4\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \
\ \ (4) \\
c + d = 2\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \
\ \ \ \ (5) \\
d = 1\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \
\ \ \ \ \ \ \ (6) \\
x + y + z + a + b + c + d = 16\ \ (7)
\end{matrix} \right.\)
Từ phương trình \((3),(4),(5),(6)\) ta được: \(a = 4;b = 3,c = 1,d =
1.\)
Thay vào phương trình \((1)\), \((2)\) ta được: \(x = 3,y = 2\).
Từ phương trình \((7)\): \(x + y + z + a + b + c + d = 16\)
\(\Leftrightarrow z + b + c + d = 16 - x -
y - a\)
\(\Leftrightarrow z + b + c + d =
7\).
Vậy số học sinh đạt điểm giỏi môn Hóa là: \(z + b + c + d = 7\).
-----------------------------------------------------------------
Việc nắm vững ứng dụng thực tế của các phép toán tập hợp nâng cao sẽ giúp bạn không chỉ học tốt môn Toán 10 mà còn phát triển kỹ năng tư duy logic và giải quyết vấn đề một cách khoa học. Hãy thường xuyên luyện tập qua các bài tập có đáp án để kiểm tra và củng cố kiến thức. Nếu bạn đang tìm kiếm thêm các dạng bài nâng cao khác, đừng ngần ngại khám phá các bài viết liên quan trên website để tiếp tục học tập hiệu quả hơn mỗi ngày!
