Ứng dụng tích vô hướng trong thực tế Toán 10 có đáp án
Vận dụng công thức tích vô hướng giải bài toán thực tế Toán 10
Trong chương trình Toán 10, phần tích vô hướng của hai vectơ không chỉ mang tính lý thuyết mà còn có nhiều ứng dụng thực tế quan trọng trong đời sống và kỹ thuật. Bài viết Ứng dụng tích vô hướng trong thực tế Toán 10 có đáp án sẽ giúp học sinh hiểu rõ cách vận dụng công thức tích vô hướng để giải quyết các bài toán thực tế, từ đó rèn luyện khả năng tư duy và áp dụng kiến thức vào các tình huống cụ thể. Ngoài ra, bài viết còn cung cấp bài tập tích vô hướng có đáp án chi tiết, giúp bạn học hiệu quả và đạt điểm cao trong các kỳ kiểm tra.
A. Ví dụ minh họa bài toán thực tế ứng dụng tích vô hướng
Ví dụ 1: Một người dùng một lực 
\(\overrightarrow{F}\) có độ lớn là 90 N làm một vật dịch chuyển một đoạn 100 m. Biết lực \(\overrightarrow{F}\) hợp với hướng dịch chuyển một góc 60°. Tính công sinh bởi lực \(\overrightarrow{F}\).
Hướng dẫn giải
Lực \(\overrightarrow{F}\) có độ lớn là 90 N.
Quãng đường dịch chuyển của vật là 100 m.
Góc tạo bởi lực \(\overrightarrow{F}\)với hướng dịch chuyển là 60°.
Vây công sinh bởi lực \(\overrightarrow{F}\) là: A = 90 . 100 . cos60° = 4500 (J).
Ví dụ 2: Một người dùng một lực \(\overrightarrow{F}\) có độ lớn là 20 N kéo một vật dịch chuyển một đoạn 50 m cùng hướng với \(\overrightarrow{F}\)Tính công sinh bởi lực \(\overrightarrow{F}\).
Hướng dẫn giải
Vì lực \(\overrightarrow{F}\) cùng hướng với hướng dịch chuyển của vật nên góc tạo bởi lực \(\overrightarrow{F}\)và hướng dịch chuyển là 0°.
Vậy công sinh bởi lực F là: A = 20 . 50 . cos0° = 1000 (J).
Ví dụ 3: Một lực \(\overrightarrow{F}\) không đổi tác động vào một vật và điểm đặt của lực chuyển động thẳng đều từ A đến B. Lực \(\overrightarrow{F}\)được phân tích thành hai lực thành phần \(\overrightarrow{F_{1}}\)và \(\overrightarrow{F_{2}}\ \ \ (\overrightarrow{F} =
\overrightarrow{F_{1}} + \overrightarrow{F_{2}})\).
a) Dựa vào tính chất của tích vô hướng, hãy giải thích vì sao công sinh bởi lực \(\overrightarrow{F}\) (đã được đề cập ở trên) bằng tổng của các công sinh bởi các lực \(\overrightarrow{F_{1}}\) và \(\overrightarrow{F_{2}}\).
b) Giả sử các lực thành phần \(\overrightarrow{F_{1}}\)và \(\overrightarrow{F_{2}}\) tương ứng cùng phương, vuông góc với phương chuyển động của vật. Hãy tìm mối quan hệ giữa các công sinh bởi lực \(\overrightarrow{F}\) và lực \(\overrightarrow{F_{1}}\).
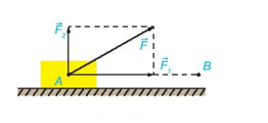
Hướng dẫn giải
a) Một lực \(\overrightarrow{F}\)tác động lên một vật làm vật dịch chuyển tính tiến theo một vectơ độ rời \(\overrightarrow{s}\)
Ta có:
Công sinh bởi lực \(\overrightarrow{F}\) là
\(A_{\overrightarrow{F}} =
\overrightarrow{F}.\overrightarrow{s} =
F.s.cos(\overrightarrow{F},\overrightarrow{s}) =
F.s.cos(\overrightarrow{F},\overrightarrow{F_{1}})\)
Mặt khác \(F.cos(\overrightarrow{F},\overrightarrow{F_{1}}) =
F_{1} \Rightarrow A_{\overrightarrow{F}} = F_{1}.s\).
Công sinh bởi lực \(\overrightarrow{F_{1}}\) là:
\(A_{\overrightarrow{F_{1}}} =
\overrightarrow{F_{1}}.\overrightarrow{s} =
F_{1}.s.cos(\overrightarrow{F_{1}},\overrightarrow{s}) =
F_{1}.s.cos0^{0} = F_{1}.s\)
Công sinh bởi lực \(\overrightarrow{F_{2}}\) là:
\(A_{\overrightarrow{F_{2}}} =
\overrightarrow{F_{2}}.\overrightarrow{s} =
F_{2}.s.cos(\overrightarrow{F_{2}},\overrightarrow{s}) =
F_{2}.s.cos90^{0} = 0\)
\(A_{\overrightarrow{F_{1}}} +
A_{\overrightarrow{F_{2}}} = F_{1}.s\)
Do đó \(A_{\overrightarrow{F}} =
A_{\overrightarrow{F_{1}}} + A_{\overrightarrow{F_{2}}}.\)
b) Ta có: \(A_{\overrightarrow{F}} =
\overrightarrow{F}.\overrightarrow{s} =
F.s.cos(\overrightarrow{F},\overrightarrow{s}) =
F.s.cos(\overrightarrow{F},\overrightarrow{F_{1}})\)
Mặt khác \(F.cos(\overrightarrow{F},\overrightarrow{F_{1}}) =
F_{1} \Rightarrow A_{\overrightarrow{F}} = F_{1}.s.\)
Ta lại có: \(A_{\overrightarrow{F_{1}}} =
\overrightarrow{F_{1}}.\overrightarrow{s} =
F_{1}.s.cos(\overrightarrow{F_{1}},\overrightarrow{s}) =
F_{1}.s.cos0^{0} = F_{1}.s \Rightarrow A_{\overrightarrow{F}} =
A_{\overrightarrow{F_{1}}}\)
B. Bài tập tự rèn luyện có đáp án chi tiết
Bài tập 1: Một người dùng một lực \(\overrightarrow{F}\) có độ lớn là 10N kéo môt chiếc xe đi quãng đường dài 100 m. Tính công sinh bởi lực \(\overrightarrow{F}\), biết rằng góc giữa vectơ \(\overrightarrow{F}\) và hướng di chuyển là 45°. (Công A (đơn vị: J) bằng tích của ba đại lượng: cường độ của lực \(\overrightarrow{F}\), độ dài quãng đường và côsin của góc giữa hai vectơ \(\overrightarrow{F}\) và độ dịch chuyển \(\overrightarrow{d}\)).
Bài tập 2: Một vật đồng thời bị ba lực tác động: lực tác động thứ nhất \(\overrightarrow{F_{1}}\) có độ lớn là 1500 N, lực tác động thứ hai \(\overrightarrow{F_{2}}\) có độ lớn là 600N, lực tác động thứ ba \(\overrightarrow{F_{3}}\) có độ lớn là 800N. Các lực này được biểu diễn bằng những vectơ như hình vẽ, với \((\overrightarrow{F_{1}},\overrightarrow{F_{2}}) =
30^{0},\ (\overrightarrow{F_{1}},\overrightarrow{F_{3}}) = 45^{0},\
(\overrightarrow{F_{2}},\overrightarrow{F_{3}}) = 75^{0}\).
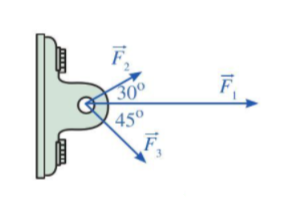
Tính độ lớn lực tổng hợp tác động lên vật (làm tròn kết quả đến hàng đơn vị.
Toàn bộ nội dung đã sẵn sàng! Nhấn Tải về để tải đầy đủ tài liệu.
------------------------------------------------
Qua bài viết Ứng dụng tích vô hướng trong thực tế Toán 10 có đáp án, bạn đã thấy rõ mối liên hệ giữa kiến thức Toán học và thực tiễn đời sống. Việc nắm vững tích vô hướng của hai vectơ giúp bạn không chỉ giải nhanh các bài tập mà còn hiểu cách Toán học được ứng dụng trong vật lý, kỹ thuật và công nghệ. Tiếp tục luyện tập với bài tập tích vô hướng có đáp án sẽ giúp bạn củng cố kỹ năng và đạt kết quả học tập vượt trội.
