VnDoc.com

Đóng

Bạn đã dùng hết 1 lần làm bài Trắc nghiệm miễn phí. Mời bạn mua tài khoản VnDoc PRO để tiếp tục! Tìm hiểu thêm

Mua VnDoc PRO chỉ từ 79.000đ

Đóng

Bạn cần đăng nhập tài khoản Thành viên VnDoc để:

- Xem đáp án

- Nhận 1 lần làm bài trắc nghiệm miễn phí!

Đăng nhập

Bài tập Trắc nghiệm giao và hợp của hai tập hợp lớp 10 Có đáp án chi tiết

Chuyên đề Toán 10 Tập hợp có đáp án

Xác định giao và hợp của hai tập hợp Toán 10

Trong chương trình Toán 10 – chuyên đề Tập hợp, dạng toán về giao và hợp của hai tập hợp là kiến thức cơ bản nhưng lại có nhiều ứng dụng quan trọng. Đây không chỉ là nền tảng để học sinh hiểu rõ bản chất các phép toán trên tập hợp, mà còn là bước đệm để tiếp cận các chuyên đề nâng cao về xác suất, thống kê và logic toán học.

Bài viết này tổng hợp bài tập trắc nghiệm giao và hợp của hai tập hợp lớp 10 có đáp án chi tiết, giúp học sinh vừa ôn tập lý thuyết, vừa rèn luyện kỹ năng làm bài nhanh – chính xác. Với hệ thống câu hỏi đa dạng, phân theo mức độ từ cơ bản đến nâng cao, đây chắc chắn là tài liệu hữu ích cho học sinh lớp 10 trong quá trình học tập và ôn luyện.

Nhận biết Thông hiểu Vận dụng Vận dụng cao

Bài kiểm tra này bao gồm 34 câu
Điểm số bài kiểm tra: 34 điểm
Xem lại kỹ lý thuyết trước khi làm bài
Chuẩn bị giấy và bút để nháp trước khi bắt đầu

00:00:00

Câu 1: Nhận biết
Xác định giao hai tập hợp
Cho tập hợp $X = \left\{ 1;5 \right\},Y = \left\{ 1;3;5 \right\}$ . Tập $X \cap Y$ là tập hợp nào sau đây?
- A.
  $\left\{ 1;3 \right\}$
- B.
  $\left\{ 1 \right\}$
- C.
  $\{ 1;3;5\}$
- D.
  $\left\{ 1;5 \right\}$
Hướng dẫn:
Vì $X \cap Y$ là tập hợp gồm các phần tử vừa thuộc X và vừa thuộc Y
Câu 2: Nhận biết
Chọn đáp án đúng
Cho tập $X = \left\{ 2;4;6;9 \right\},Y = \left\{ 1;2;3;4 \right\}$ . Tập nào sau đây bằng tập $X\backslash Y$ ?
- A.
  $\left\{ 6;9 \right\}$ 9
- B.
  $\left\{ 1;3;6;9 \right\}$
- C.
  $\left\{ 1;2;3;5 \right\}$
- D.
  $\left\{ 1 \right\}$
Hướng dẫn:
Vì $X\backslash Y$ là tập hợp các phần tử thuộc X mà không thuộc Y
Câu 3: Nhận biết
Tìm giao của hai tập hợp
Cho tập hợp $X = \left\{ a;b \right\},Y = \left\{ a;b;c \right\}$ . $X \cup Y$ là tập hợp nào sau đây?
- A.
  $\{ a;b;c\}$
- B.
  $\left\{ a;b;c;d \right\}$
- C.
  $\left\{ a;b \right\}$
- D.
  $\left\{ c \right\}$
Hướng dẫn:
Vì $X \cup Y$ là tập hợp gồm các phần tử thuộc X hoặc thuộc Y
Câu 4: Thông hiểu
Tìm mệnh đề sai
Cho hai tập hợp A và B khác rỗng thỏa mãn: $A \subset B$ . Trong các mệnh đề sau mệnh đề nào sai?
- A.
  $B\backslash A = B$
- B.
  $A \cap B = A$
- C.
  $A\backslash B = \varnothing$
- D.
  $A \cup B = B$
Hướng dẫn:
Vì $B\backslash A$ gồm các phần tử thuộc B và không thuộc A
Câu 5: Thông hiểu
Tìm mệnh đề đúng
Cho ba tập hợp: $F = \left\{ x\mathbb{\in R}|f(x) = 0 \right\},$ $G = \left\{ x\mathbb{\in R}|g(x) = 0 \right\},$ $H = \left\{ x\mathbb{\in R}|f(x) + g(x) = 0 \right\}$ .

Mệnh đề nào sau đây là đúng?
- A.
  $H = G\backslash F$
- B.
  $H = F \cup G$
- C.
  $H = F\backslash G$
- D.
  $H = F \cap G$
Hướng dẫn:
Vì $\left| f(x) \right| + \left| g(x) \right| = 0 \Leftrightarrow \left\{ \begin{matrix} f(x) = 0 \\ g(x) = 0 \end{matrix} \right.$ mà $F \cap G = \left\{ x\mathbb{\in R}|f(x)\ và\ g(x) = 0 \right\}$
Câu 6: Vận dụng
Tìm số phần tửu chung của hai tập hợp
Cho tập hợp $A = \left\{ x\mathbb{\in R}|\frac{2x}{x^{2} + 1} \geq 1 \right\}$ ; B là tập hợp tất cả các giá trị nguyên của b để phương trình $x^{2} - 2bx + 4 = 0$ vô nghiệm. Số phần tử chung của hai tập hợp trên là:
- A.
  1
- B.
  3
- C.
  2
- D.
  Vô số
Hướng dẫn:
Ta có: $\frac{2x1}{x^{2} + 1} \geq 1 \Leftrightarrow 2x \geq x^{2} + 1 \Leftrightarrow x^{2} - 2x + 1 \leq 0 \Leftrightarrow (x - 1)^{2} \leq 0 \Leftrightarrow x = 1$

Phương trình $x^{2} - 2bx + 4 = 0$ có $\Delta' = b^{2} - 4$

Phương trình vô nghiệm $\Leftrightarrow b^{2} - 4 < 0 \Leftrightarrow b^{2} < 4 \Leftrightarrow - 2 < b < 2$

Có $b = 1$ là phần tử chung duy nhất của hai tập hợp.
Câu 7: Nhận biết
Chọn đáp án đúng
Cho hai tập hợp $X = \left\{ 1;2;3;4 \right\},Y = \left\{ 1;2 \right\}$ . $C_{X}Y$ là tập hợp sau đây?
- A.
  $\left\{ 3;4 \right\}$
- B.
  $\left\{ 1;2;3;4 \right\}$
- C.
  $\left\{ 1;2 \right\}$
- D.
  $\varnothing$
Hướng dẫn:
Vì $Y \subset X$ nên $C_{X}Y = X\backslash Y = \left\{ 3;4 \right\}$
Câu 8: Thông hiểu
Chọn phương án thích hợp
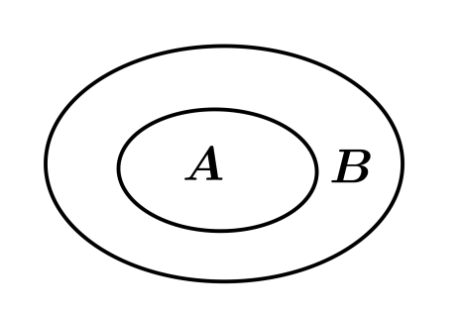
Cho A, B, C là ba tập hợp được minh họa bằng biểu đồ ven như hình vẽ.

Phần gạch sọc trong hình vẽ là tập hợp nào sau đây?
- A.
  $(A \cap B) \cup C$
- B.
  $(A \cap B)\backslash C$
- C.
  $(A\backslash C) \cup (A\backslash B)$
- D.
  $(A \cup B)\backslash C$
Hướng dẫn:
Vì với mỗi phần tử $x$ thuộc phần gạch sọc thì ta thấy:

$\left\{ \begin{matrix} x \in A \\ x \in B \\ x \notin C \end{matrix} \right.\ \Rightarrow x \in (A \cap B)\backslash C$ .
Câu 9: Thông hiểu
Xác định số tập hợp X thỏa mãn điều kiện đề bài
Cho hai tập hợp $A = \left\{ 0;2 \right\}$ và $B = \left\{ 0;1;2;3;4 \right\}$ . Số tập hợp X thỏa mãn $A \cup X = B$ là:
- A.
  4
- B.
  3
- C.
  2
- D.
  5
Hướng dẫn:

Vì $A \cup X = B$ nên bắt buộc X phải chứa các phần tử $\left\{ 1;3;4 \right\}$ và $X \subset B$ .

Vậy X có 3 tập hợp đó là: $\left\{ 1;3;4 \right\},\left\{ 1;2;3;4 \right\},\left\{ 0;1;2;3;4 \right\}$ .
Câu 10: Thông hiểu
Xác định số tập hợp X
Cho hai tập hợp $A = \left\{ 0;1 \right\}$ và $B = \left\{ 0;1;2;3;4 \right\}$ . Số tập hợp X thỏa mãn $X \subset C_{B}A$ là:
- A.
  8
- B.
  3
- C.
  6
- D.
  5
Hướng dẫn:
Ta có $C_{B}A = B\backslash A = \left\{ 2;3;4 \right\}$ có 3 phần tử nên số tập con $X$ có $2^{3} = 8$ (tập).
Câu 11: Thông hiểu
Tìm số tập X thỏa mãn yêu cầu bài toán
Cho tập hợp $A = \left\{ 1;2;3;4;5 \right\}$ . Tìm số tập hợp X sao cho $A\backslash X = \left\{ 1;3;5 \right\}$ và $X\backslash A = \left\{ 6;7 \right\}$ .
- A.
  4
- B.
  3
- C.
  2
- D.
  1
Hướng dẫn:
Vì $A\backslash X = \left\{ 1;3;5 \right\}$ nên X phải chứa hai phần tử 2; 4 và X không chứa các phần tử 1; 3; 5.

Mặt khác $X\backslash A = \left\{ 6;7 \right\}$ vậy X phải chứa 6; 7 và các phần tử khác nếu có phải thuộc $A$ .

Vậy $X = \left\{ 2;4;6;7 \right\}$ .
Câu 12: Thông hiểu
Tìm mệnh đề sai
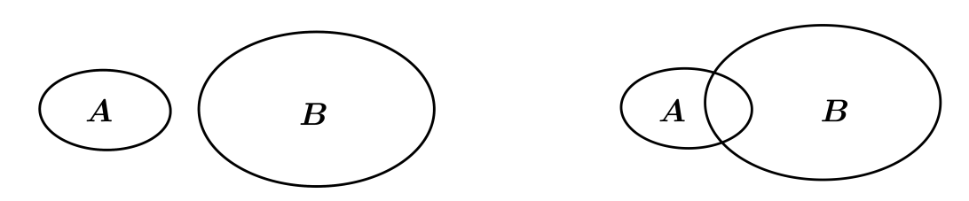
Ký hiệu $|X|$ là số phần tử của tập hợp X. Mệnh đề nào sai trong các mệnh đề sau?
- A.
  $A \cap B = \varnothing \Rightarrow |A| + |B| = |A \cup B| + |A \cap B|$
- B.
  $A \cap B \neq \varnothing \Rightarrow |A| + |B| = |A \cup B| + |A \cap B|$
- C.
  $A \cap B \neq \varnothing \Rightarrow |A| + |B| = |A \cup B| - |A \cap B|$
- D.
  $A \cap B = \varnothing \Rightarrow |A| + |B| = |A \cup B|$
Hướng dẫn:
Kiểm tra các đáp án bằng cách vẽ biểu đồ Ven cho hai trường hợp $A \cap B = \varnothing$ và $A \cap B \neq \varnothing$
Câu 13: Vận dụng
Chọn kết quả chính xác
Một lớp học có 25 học sinh giỏi môn Toán, 23 học sinh giỏi môn Lý, 14 học sinh giỏi cả môn Toán và Lý và có 6 học sinh không giỏi môn nào cả. Hỏi lớp đó có bao nhiêu học sinh?
- A.
  54
- B.
  40
- C.
  26
- D.
  68
Hướng dẫn:

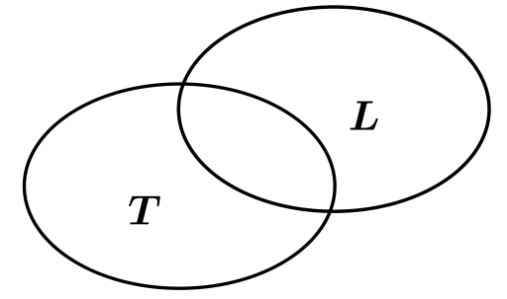
Gọi T, L lần lượt là tập hợp các học sinh giỏi Toán và các học sinh giỏi Lý.

Ta có:

$|T|$ : là số học sinh giỏi Toán

$|L|$ : là số học sinh giỏi Lý

$|T \cap L|$ : là số học sinh giỏi cả hai môn Toán và Lý

Khi đó số học sinh của lớp là: $|T \cup L| + 6$ .

Mà $|T \cup L| = |T| + |L| - |T \cap L| = 25 + 23 - 14 = 34$ .

Vậy số học sinh của lớp là $34 + 6 = 40$ .
Câu 14: Vận dụng cao
Tìm số học sinh thỏa mãn yêu cầu
Lớp 10A có 45 học sinh trong đó có 25 em học giỏi môn Toán, 23 em học giỏi môn Lý, 20 em học giỏi môn Hóa, 11 em học giỏi cả môn Toán và môn Lý, 8 em học giỏi cả môn Lý và môn Hóa, 9 em học giỏi cả môn Toán và môn Hóa. Hỏi lớp 10A có bao nhiêu bạn học giỏi cả ba môn Toán, Lý, Hóa, biết rằng mỗi học sinh trong lớp học giỏi ít nhất một trong 3 môn Toán, Lý, Hóa?
- A.
  6
- B.
  5
- C.
  4
- D.
  3
Hướng dẫn:
Gọi T, L, H lần lượt là tập hợp các học sinh giỏi môn Toán, Lý, Hóa.

Khi đó tương tự Ví dụ 13 ta có công thức:

$|T \cup L \cup H| = |T| + |L| + |H| - |T \cap L| - |L \cap H| - |H \cap T| + |T \cap L \cap H|$

$\Leftrightarrow 45 = 25 + 23 + 20 - 11 - 8 - 9 + |T \cap L \cap H| \Leftrightarrow |T \cap L \cap H| = 5$

Vậy có 5 học sinh giỏi cả 3 môn.
Câu 15: Thông hiểu
Xác định mệnh đề đúng
Cho tập hợp $A = \left\{ 1;2;3;4 \right\},B = \left\{ 0;2;4;6 \right\}$ . Mệnh đề nào sau đây là đúng?
- A.
  $A \subset B$
- B.
  $A \cup B = \left\{ 0;1;2;3;4;5;6 \right\}$
- C.
  $A\backslash B = \left\{ 0;6 \right\}$
- D.
  $A \cap B = \left\{ 2;4 \right\}$
Hướng dẫn:
Ta thấy $A \cap B = \left\{ 2;4 \right\}$ .
Câu 16: Nhận biết
Tìm khẳng định sai
Ký hiệu H là tập hợp các học sinh của lớp 10A. T là tập hợp các học sinh nam, G là tập hợp các học sinh nữ của lớp 10A. Khẳng định nào sau đây sai?
- A.
  $T \cap G = \varnothing$
- B.
  $T \cup G = H$
- C.
  $H\backslash T = G$
- D.
  $G\backslash T = \varnothing$
Hướng dẫn:
Vì $G\backslash T = G$ nên câu sai là: $G\backslash T = \varnothing$ .
Câu 17: Thông hiểu
Tìm câu sai
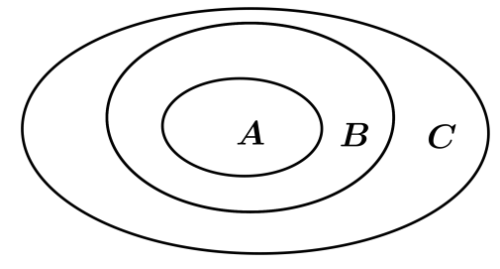
Cho A, B, C là ba tập hợp. Mệnh đề nào sau đây là sai?
- A.
  $A \subset B \Rightarrow A \cup C \subset B \cup C$
- B.
  $A \subset B,B \subset C \Rightarrow A \subset C$
- C.
  $A \subset B \Rightarrow C\backslash A \subset C\backslash B$
- D.
  $A \subset B \Rightarrow A \cap C \subset B \cap C$
Hướng dẫn:
Ta có thể dùng biểu đồ Ven ta thấy $A \subset B \Rightarrow C\backslash A \subset C\backslash B$
Câu 18: Thông hiểu
Tìm tập hợp X
Cho tập hợp $A = \left\{ a;b;c \right\}$ và $B = \left\{ a;b;c;d;e \right\}$ . Có tất cả bao nhiêu tập hợp X thỏa mãn $A \subset X \subset B$ ?
- A.
  5
- B.
  8
- C.
  4
- D.
  6
Hướng dẫn:
Vì $A \subset X$ nên X phải chứa 3 phần tử $\left\{ a;b;c \right\}$ của $A$ .

Mặt khác $X \subset B$ nên $X$ chỉ có thể lấy các phần tử a, b, c, d, e.

Vậy X là một trong các tập hợp sau:

$\left\{ a;b;c \right\},\left\{ a;b;c;d \right\}$ , $\left\{ a;b;c;e \right\}$ , $\left\{ a;b;c;d;e \right\}$ .
Câu 19: Nhận biết
Chọn phương án chính xác
Cho hai tập hợp $A = \left\{ 1;2;3;4;5 \right\};B = \left\{ 1;3;5;7;9 \right\}$ . Tập nào sau đây bằng tập $A \cap B$ ?
- A.
  $\left\{ 1;3;5 \right\}$
- B.
  $\left\{ 2;4;6;8 \right\}$
- C.
  $\left\{ 1;2;3;4;5;7;9 \right\}$
- D.
  $\left\{ 1;2;3;4;5 \right\}$
Hướng dẫn:
Vì $A \cap B$ gồm các phần tử vừa thuộc $A$ vừa thuộc $B$ .
Câu 20: Thông hiểu
Chọn phương án đúng
Cho tập hợp $A = \left\{ 2;4;6;9 \right\},B = \left\{ 1;2;3;4 \right\}$ . Tập nào sau đây bằng tập $A\backslash B$ ?
- A.
  $\varnothing$
- B.
  $\left\{ 6;9 \right\}$
- C.
  $\left\{ 1;2;3;5 \right\}$
- D.
  $\left\{ 1;2;3;4;6;9 \right\}$
Hướng dẫn:
Vì $A\backslash B = \left\{ x|x \in A\ va\text{ }x \notin B \right\}$ nên đáp án đúng là: $\left\{ 6;9 \right\}$
Câu 21: Thông hiểu
Chọn kết quả đúng
Cho các tập hợp $A = \left\{ x\mathbb{\in R}:x^{2} - 7x + 6 = 0 \right\},B = \left\{ x\mathbb{\in N}:|x| < 4 \right\}$ . Khi đó:
- A.
  $A \cup B = A$
- B.
  $A\backslash B \subset A$
- C.
  $A \cap B = A \cup B$
- D.
  $B\backslash A = \varnothing$
Hướng dẫn:
Ta có:

$A = \left\{ 1;6 \right\},B = \left\{ x\mathbb{\in N}\backslash|x| < 4 \right\}$

$\Rightarrow B = \left\{ 0;1;2;3 \right\} \Rightarrow A\backslash B = \left\{ 6 \right\} \Rightarrow A\backslash B \subset A$ .
Câu 22: Thông hiểu
Tìm số học sinh thỏa mãn yêu cầu
Một lớp học có 25 học sinh chơi bóng đá, 23 học sinh chơi bóng bàn, 14 học sinh chơi cả bóng đá và bóng bàn và 6 học sinh không chơi môn nào. Số học sinh chỉ chơi 1 môn thể thao là?
- A.
  48
- B.
  34
- C.
  28
- D.
  20
Hướng dẫn:
Gọi A là tập hợp các học sinh chơi bóng đá

B là tập hợp các học sinh chơi bóng bàn

C là tập hợp các học sinh không chơi môn nào

Khi đó số học sinh chỉ chơi bóng đá là: $|A| + |B| - 2|A \cap B| = 25 + 23 - 2.14 = 20$
Câu 23: Thông hiểu
Khẳng định đúng
Trong các khẳng định sau khẳng định nào đúng:
- A.
  $\mathbb{N}^{*}\mathbb{\cap Q =}\mathbb{N}^{*}$ .
- B.
  $\mathbb{N}^{*}\mathbb{\cup N = Z}$ .
- C.
  $\mathbb{R}\backslash\mathbb{Q = N}$ .
- D.
  $\mathbb{N}^{*}\mathbb{\cap Z = Z}$ .
Hướng dẫn:
Vì $\mathbb{N}^{*}\mathbb{\subset Q \Rightarrow}\mathbb{N}^{*}\mathbb{\cap Q =}\mathbb{N}^{*}$ nên khẳng định đúng là: $\mathbb{N}^{*}\mathbb{\cap Q =}\mathbb{N}^{*}$
Câu 24: Thông hiểu
Xác định kết quả sai
Chọn kết quả sai trong các kết quả sau:
- A.
  $A \cap B = A \Leftrightarrow A \subset B.$
- B.
  $A\backslash B = A \Leftrightarrow A \cap B = \varnothing.$
- C.
  $B\backslash A = B \Leftrightarrow A \cap B = \varnothing.$
- D.
  $A \cup B = A \Leftrightarrow A \subset B.$
Hướng dẫn:
Phương án sai là phương án $A \cup B = A \Leftrightarrow A \subset B.$

Vì $A \cup B = A \Leftrightarrow A \supset B.$
Câu 25: Thông hiểu
Chọn đáp án đúng
Cho $X = \left\{ 7;2;8;4;9;12 \right\}$ ; $Y = \left\{ 1;3;7;4 \right\}$ . Tập nào sau đây bằng tập $X \cap Y$ ?
- A.
  $\left\{ 2;8;9;12 \right\}$ .
- B.
  $\left\{ 1;3 \right\}$ .
- C.
  $\left\{ 1;2;3;4;8;9;7;12 \right\}$ .
- D.
  $\left\{ 4;7 \right\}$ .
Hướng dẫn:
Ta có:

$X = \left\{ 7;2;8;4;9;12 \right\},\ \ \ \ Y = \left\{ 1;3;7;4 \right\} \Rightarrow X \cap Y = \left\{ 7;4 \right\}.$
Câu 26: Nhận biết
Phương án nào đúng
Cho hai tập hợp $A = \left\{ 2,4,6,9 \right\}$ và $B = \left\{ 1,2,3,4 \right\}$ .Tập hợp $A\backslash B$ bằng tập nào sau đây?
- A.
  $\left\{ 6;9 \right\}.$
- B.
  $A = \left\{ 1,2,3,5 \right\}$ .
- C.
  $\varnothing.$
- D.
  $\left\{ 1;3;6;9 \right\}.$
Hướng dẫn:
Ta có:

$A = \left\{ 2,4,6,9 \right\},\ \ \ \ B = \left\{ 1,2,3,4 \right\} \Rightarrow A\backslash B = \left\{ 6,9 \right\}.$
Câu 27: Thông hiểu
Chọn phương án chính xác
Cho $A = \left\{ 0;1;2;3;4 \right\},B = \left\{ 2;3;4;5;6 \right\}.$ Tập hợp $(A\backslash B) \cup (B\backslash A)$ bằng?
- A.
  $\left\{ 5;6 \right\}.$
- B.
  $\left\{ 0;1;5;6 \right\}.$
- C.
  $\left\{ 2;3;4 \right\}.$
- D.
  $\left\{ 1;2 \right\}.$
Hướng dẫn:
Ta có:

$A = \left\{ 0;1;2;3;4 \right\},B = \left\{ 2;3;4;5;6 \right\}.$

$A\backslash B = \left\{ 0;1 \right\},\ \ B\backslash A = \left\{ 5;6 \right\} \Rightarrow (A\backslash B) \cup (B\backslash A) = \left\{ 0;1;5;6 \right\}$
Câu 28: Thông hiểu
Xác định tập hợp
Cho $A = \left\{ 0;1;2;3;4 \right\},B = \left\{ 2;3;4;5;6 \right\}.$ Tập hợp $A\backslash B$ bằng:
- A.
  $\left\{ 0;1 \right\}.$
- B.
  $\left\{ 0 \right\}.$
- C.
  $\left\{ 1;5 \right\}.$
- D.
  $\left\{ 1;2 \right\}.$
Hướng dẫn:
Ta có:

$A = \left\{ 0;1;2;3;4 \right\},\ \ \ \ B = \left\{ 2;3;4;5;6 \right\} \Rightarrow A\backslash B = \left\{ 0;1 \right\}$
Câu 29: Thông hiểu
Chọn đáp án đúng
Cho $A = \left\{ 0;1;2;3;4 \right\},B = \left\{ 2;3;4;5;6 \right\}.$ Tập hợp $B\backslash A$ bằng:
- A.
  $\left\{ 5;6 \right\}.$
- B.
  $\left\{ 2;3;4 \right\}.$
- C.
  $\left\{ 0;1 \right\}.$
- D.
  $\left\{ 5 \right\}.$
Hướng dẫn:
Ta có:

$A = \left\{ 0;1;2;3;4 \right\},\ \ \ \ B = \left\{ 2;3;4;5;6 \right\} \Rightarrow B\backslash A = \left\{ 5;6 \right\}.$
Câu 30: Nhận biết
Chọn kết quả đúng
Cho $A = \left\{ 1;5 \right\};B = \left\{ 1;3;5 \right\}.$ Chọn kết quả đúng trong các kết quả sau
- A.
  $A \cap B = \left\{ 1;3;5 \right\}.$
- B.
  $A \cap B = \left\{ 1;5 \right\}.$
- C.
  $A \cap B = \left\{ 1 \right\}.$
- D.
  $A \cap B = \left\{ 1;3 \right\}.$
Hướng dẫn:
Ta có:

$A = \left\{ 1;5 \right\};B = \left\{ 1;3;5 \right\}.$ Suy ra $A \cap B = \left\{ 1;5 \right\}.$
Câu 31: Vận dụng
Xác định giao của hai tập hợp
Cho $A = \left\{ \left. \ x\mathbb{\in N}\right|\left( 2x - x^{2} \right)\left( 2x^{2} - 3x - 2 \right) = 0\right\};$ $B = \left\{ \left. \ n \in \mathbb{N}^{*} \right|3 < n^{2}< 30 \right\}$ . Khi đó tập hợp $A \cap B$ bằng:
- A.
  $\left\{ 2 \right\}.$
- B.
  $\left\{ 2;4 \right\}.$
- C.
  $\left\{ 3 \right\}.$
- D.
  $\left\{ 4;5 \right\}.$
Hướng dẫn:
Ta có:

$A = \left\{ \left. \ x\mathbb{\in N}\right|\left( 2x - x^{2} \right)\left( 2x^{2} - 3x - 2 \right) = 0\right\}$

$\Leftrightarrow A = \left\{ 0;\ 2 \right\}$

$B = \left\{ \left. \ n \in\mathbb{N}^{*} \right|3 < n^{2} < 30 \right\}$

$\Leftrightarrow B =\left\{ 1;\ 2;\ 3;\ 4;5\ \right\} \Rightarrow A \cap B = \left\{ 2\right\}.$
Câu 32: Vận dụng cao
Tìm a thỏa mãn điều kiện phép toán
Cho hai tập $A = \lbrack 0;5\rbrack$ ; $B = (2a;3a + 1\rbrack$ , $a > - 1$ . Với giá trị nào của $a$ thì $A \cap B \neq \varnothing$
- A.
  $- \frac{1}{3} \leq a < \frac{5}{2}$ .
- B.
  $- \frac{1}{3} \leq a \leq \frac{5}{2}$ .
- C.
  $\left\lbrack \begin{matrix} a < \frac{5}{2} \\ a \geq - \frac{1}{3} \end{matrix} \right.$ .
- D.
  $\left\lbrack \begin{matrix} a \geq \frac{5}{2} \\ a < - \frac{1}{3} \end{matrix} \right.$ .
Hướng dẫn:
Ta tìm $A \cap B = \varnothing \Leftrightarrow \left\{ \begin{matrix} \left\lbrack \begin{matrix} 2a \geq 5 \\ 3a + 1 < 0 \end{matrix} \right.\ \\ a > - 1 \end{matrix} \right.$

$\Leftrightarrow \left\{ \begin{matrix} \left\lbrack \begin{matrix} a \geq \frac{5}{2} \\ a < - \frac{1}{3} \end{matrix} \right.\ \\ a > - 1 \end{matrix} \right.\ \Rightarrow \left\lbrack \begin{matrix} a \geq \frac{5}{2} \\ - 1 < a < - \frac{1}{3} \end{matrix} \right.$

$\Rightarrow A \cap B \neq \varnothing \Leftrightarrow - \frac{1}{3} \leq a < \frac{5}{2}$
Câu 33: Vận dụng cao
Định m thỏa mãn phép toán
Cho 2 tập khác rỗng $A = (m - 1;4\rbrack;B = ( - 2;2m + 2),m\mathbb{\in R}$ . Tìm m để $A \cap B \neq \varnothing$
- A.
  $- 1 < m < 5$ .
- B.
  $1 < m < 5$ .
- C.
  $- 2 < m < 5$ .
- D.
  $m > - 3$ .
Hướng dẫn:
Đáp án $- 1 < m < 5$ đúng vì:

Với 2 tập khác rỗng A, B ta có điều kiện

$\left\{ \begin{matrix} m - 1 < 4 \\ 2m + 2 > - 2 \end{matrix} \right.\ \Leftrightarrow \left\{ \begin{matrix} m < 5 \\ m > - 2 \end{matrix} \right.\ \Leftrightarrow - 2 < m < 5$ .

Để $A \cap B \neq \varnothing \Leftrightarrow m - 1 < 2m + 2 \Leftrightarrow m > - 3$ .

So với kết quả của điều kiện thì $- 2 < m < 5$ .
Câu 34: Vận dụng
Chọn phương án đúng
Cho số thực $a < 0$ . Điều kiện cần và đủ để $( - \infty;9a) \cap \left( \frac{4}{a}; + \infty \right) \neq \varnothing$ là:
- A.
  $- \frac{2}{3} \leq a < 0.$
- B.
  $- \frac{3}{4} \leq a < 0.$
- C.
  $- \frac{2}{3} < a < 0.$
- D.
  $- \frac{3}{4} < a < 0.$
Hướng dẫn:
Ta có:

$( - \infty;9a) \cap \left( \frac{4}{a}; + \infty \right) \neq \varnothing\ \ (a < 0) \Leftrightarrow \ \ \frac{4}{a} < 9a$

$\Leftrightarrow \ \ \frac{4}{a} - 9a\ \ < 0\ \Leftrightarrow \frac{4 - 9a²}{a} < 0$

$\Leftrightarrow \left\{ \begin{matrix} 4 - 9a² > 0 \\ a < 0\ \ \end{matrix} \right.\ \Leftrightarrow - \frac{2}{3} < a < 0$ .

Chúc mừng Bạn đã hoàn thành bài!

Kết quả làm bài:

Nhận biết (24%):

2/3
Thông hiểu (56%):

2/3
Vận dụng (12%):

2/3
Vận dụng cao (9%):

2/3

Thời gian làm bài: 00:00:00
Số câu làm đúng: 0
Số câu làm sai: 0
Điểm số: 0
Điểm thưởng: 0

Làm lại

Chia sẻ bởi:
Đen2017

1

15

Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!

Sắp xếp theo

Xóa Đăng nhập để Gửi

Chuyên đề Toán 10

Xem thêm

Mầm non

Lớp 1

Lớp 2

Lớp 3

Lớp 4

Lớp 5

Lớp 6

Lớp 7

Lớp 8

Lớp 9

Lớp 10

Lớp 11

Lớp 12

Thi vào lớp 6

Thi vào lớp 10

Thi Tốt Nghiệp THPT

Đánh Giá Năng Lực

Khóa Học Trực Tuyến

Hỏi bài

Trắc nghiệm Online

Tiếng Anh

Thư viện Học liệu

Bài tập Cuối tuần

Bài tập Hàng ngày

Thư viện Đề thi

Giáo án - Bài giảng

Tất cả danh mục

Bài tập Trắc nghiệm giao và hợp của hai tập hợp lớp 10 Có đáp án chi tiết

Xác định giao và hợp của hai tập hợp Toán 10

Chúc mừng Bạn đã hoàn thành bài!

A. CHUYÊN ĐỀ TỰ LUẬN

B. CHUYÊN ĐỀ TRẮC NGHIỆM

Lớp 10

Toán lớp 10

Chuyên đề Toán 10

Chuyên đề Toán 10

Tìm m để đường thẳng cắt Parabol tại hai điểm phân biệt

Xác định Parabol y = ax^2 + bx + c

Bài tập tích vô hướng của hai vectơ

Phương trình tổng quát của đường thẳng

Xác định vectơ chỉ phương của đường thẳng

Viết phương trình tham số, phương trình chính tắc của đường thẳng