Tâm đường tròn nội tiếp tam giác
Đường tròn nội tiếp tam giác
Trong chương Đường tròn nội tiếp tam giác – Toán 10, kiến thức về tâm đường tròn nội tiếp tam giác giữ vai trò nền tảng, xuất hiện xuyên suốt trong nhiều dạng bài từ cơ bản đến nâng cao. Việc xác định đúng vị trí tâm không chỉ giúp giải nhanh các bài toán hình học mà còn hỗ trợ suy luận chính xác về độ dài, góc và tính đối xứng trong tam giác.
Tuy nhiên, nhiều học sinh thường nhầm lẫn giữa tâm nội tiếp với các tâm đặc biệt khác như trọng tâm, trực tâm hay tâm đường tròn ngoại tiếp, dẫn đến áp dụng sai phương pháp. Xuất phát từ thực tế đó, bài viết này sẽ giúp bạn hiểu rõ khái niệm tâm đường tròn nội tiếp tam giác, cách xác định tâm bằng đường phân giác, cũng như ý nghĩa hình học quan trọng của điểm đặc biệt này. Qua đó, người học có thể nắm chắc bản chất và vận dụng hiệu quả khi làm bài tập Toán 10 và các kỳ kiểm tra, thi cử.
Bản quyền thuộc về VnDoc.
Nghiêm cấm mọi hình thức sao chép nhằm mục đích thương mại.
1. Đường tròn nội tiếp tam giác
- Đường tròn nội tiếp tam giác là đường tròn lớn nhất nằm trong tam giác, đường tròn tiếp xúc với cả 3 cạnh của tam giác.
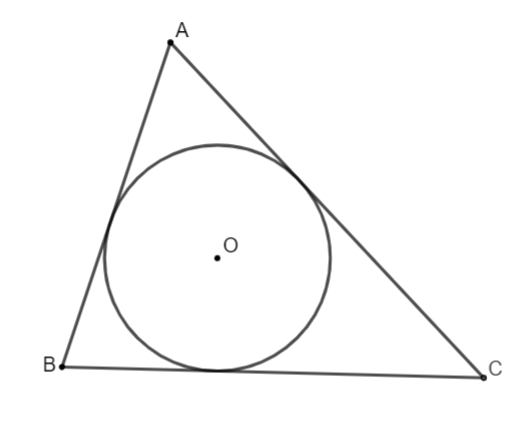
2. Cách tìm tâm đường tròn nội tiếp tam giác
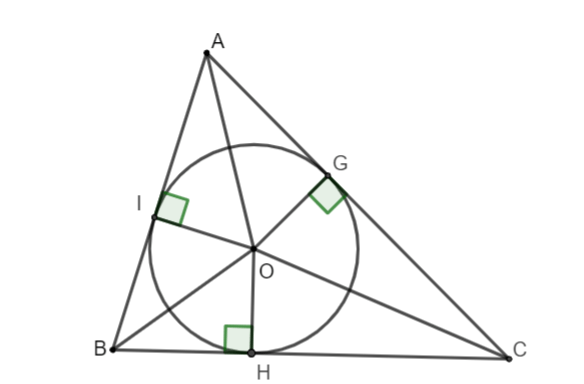
- Tâm đường tròn nội tiếp tam giác là giao của ba đường phân giác trong.
Công thức tính tâm đường đường tròn nội tiếp tam giác ABC là: 
\(\left\{ {\begin{array}{*{20}{c}}
{{x_O} = \dfrac{{AB.{x_C} + AC.{x_B} + BC.{x_A}}}{{AB + AC + BC}}} \\
{{y_O} = \dfrac{{AB.{y_C} + AC.{y_B} + BC.{y_A}}}{{AB + AC + BC}}}
\end{array}} \right.\)
Ví dụ: Trong mặt phẳng tọa độ Oxy, cho tam giác ABC với A(4; -1), B(1; 5), C(-4; -5). Tìm tâm đường tròn nội tiếp tam giác ABC.
Hướng dẫn giải
Gọi I là tâm đường tròn nội tiếp tam giác ABC.
Độ dài các cạnh tam giác: \(AB = 3\sqrt 5 ;AC = 4\sqrt 5 ;BC = 5\sqrt 5\)
Khi đó ta có:
\(\left\{ {\begin{array}{*{20}{c}}
{{x_O} = \dfrac{{3\sqrt 5 .\left( { - 4} \right) + 4\sqrt 5 .1 + 5\sqrt 5 .4}}{{3\sqrt 5 + 4\sqrt 5 + 5\sqrt 5 }} = 1} \\
{{y_O} = \dfrac{{3\sqrt 5 .\left( { - 5} \right) + 4\sqrt 5 .5 + 5\sqrt 5 .\left( { - 1} \right)}}{{3\sqrt 5 + 4\sqrt 5 + 5\sqrt 5 }} = 0}
\end{array}} \right. \Rightarrow I\left( {1;0} \right)\)
Vậy tâm đường tròn nội tiếp tam giác ABC là điểm I (1; 0)
3. Bán kính đường tròn nội tiếp tam giác
- Cho tam giác ABC có độ dài các cạnh AB = c; AC = b, BC = a
Gọi p là nửa chu vi tam giác ABC \(\Rightarrow p = \frac{{a + b + c}}{2}\)
Công thức bán kính đường tròn ngoại tiếp:
\(\begin{matrix}
r = \dfrac{S}{p} \hfill \\
r = \left( {p - a} \right).\tan \dfrac{{\widehat A}}{2} = \left( {p - b} \right).\tan \dfrac{{\widehat B}}{2} = \left( {p - c} \right).\tan \dfrac{{\widehat C}}{2} \hfill \\
r = \sqrt {\dfrac{{\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)}}{p}} \hfill \\
\end{matrix}\)
Ví dụ: Tính bán kính đường tròn nội tiếp tam giác ABC biết AB = 2, AC = 3, BC = 4
Hướng dẫn giải
\(\begin{matrix} p = \dfrac{{2 + 3 + 4}}{2} = \dfrac{9}{2} \hfill \\ \Rightarrow r = \sqrt {\dfrac{{\left( {p - 2} \right)\left( {p - 3} \right)\left( {p - 4} \right)}}{p}} = \sqrt {\frac{{\left( {\dfrac{9}{2} - 2} \right)\left( {\dfrac{9}{2} - 3} \right)\left( {\dfrac{9}{2} - 4} \right)}}{{\dfrac{9}{2}}}} = \dfrac{{\sqrt {15} }}{6} \hfill \\ \end{matrix}\)
4. Phương trình đường tròn nội tiếp tam giác
- Nhắc lại:
+ Phương trình đường tròn tâm I(a; b), bán kính R: \({\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = {R^2}\)
+ Phương trình đường phân giác của góc tạo bởi hai đường thẳng \(\left\{ {\begin{array}{*{20}{c}}
{\left( {{d_1}} \right):ax + by + c = 0} \\
{\left( {{d_2}} \right):a'x + b'y + c' = 0}
\end{array}} \right.\) là:
\(\frac{{ax + by + c}}{{\sqrt {{a^2} + {b^2}} }} = \pm \frac{{a'x + b'y + c'}}{{\sqrt {a{'^2} + b{'^2}} }}\)
Viết phương trình đường tròn nội tiếp tam giác ABC biết tọa độ các đỉnh A, B, C
Bước 1: Viết phương trình hai đường phân giác trong góc A và B
Bước 2: Tâm I là giao điểm của hai đường phân giác trên
Bước 3: Tính khoảng cách từ I đến một cạnh của tam giác ta được bán kính
Bước 4: Viết phương trình đường tròn.
Ví dụ: Viết phương trình đường tròn nội tiếp tam giác \(OAB\), biết tọa độ \(A(8;0),B(0;6)\)?
Hướng dẫn giải
Ta có: \(OA = 8;OB = 6;AB = \sqrt{8^{2} +
6^{2}} = 10\)
Mặt khác \(\frac{1}{2}OA.OB = p.r\) (vì cùng bằng diện tích tam giác ABO)
Suy ra \(r = \frac{OA.OB}{OA + OB + AB} =
2\)
Dễ thấy đường tròn cần tìm có tâm thuộc góc phần tư thứ nhất và tiếp xúc với hai trục tọa độ nên tâm của đường tròn có tọa độ \((2;2)\)
Vậy phương trình đường tròn nội tiếp tam giác OAB là: \((x - 2)^{2} + (y - 2)^{2} = 4\)
Ví dụ: Trong mặt phẳng tọa độ Oxy, cho tam giác \(ABC\) có tọa độ trọng tâm \(G\left( \frac{7}{3};\frac{4}{3} \right)\) và phương trình đường thẳng \(AB:x - y + 1 =
0\). Biết rằng tam giác \(ABC\) nội tiếp đường tròn tâm \(I(2;1)\). Xác định tọa độ điểm C?
Hướng dẫn giải
Hình vẽ minh họa
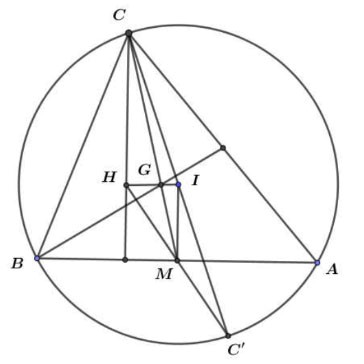
Gọi C’ là điểm đối xứng với C qua I, M là trung điểm của AB và H là trực tâm tam giác ABC
Dễ dàng chứng minh được G cũng là trọng tâm giác CC’H
Suy ra \(\overrightarrow{IH} =
3\overrightarrow{IG} \Leftrightarrow \left\{ \begin{matrix}
x_{H} - x_{I} = 3\left( x_{G} - x_{I} \right) \\
y_{H} - y_{I} = 3\left( y_{G} - y_{I} \right) \\
\end{matrix} \right.\)
\(\Leftrightarrow \left\{ \begin{matrix}
x_{H} - 2 = 3\left( \dfrac{7}{3} - 2 \right) \\
y_{H} - 1 = 3\left( \dfrac{4}{3} - 1 \right) \\
\end{matrix} \right.\ \Leftrightarrow \left\{ \begin{matrix}
x_{H} = 3 \\
y_{H} = 2 \\
\end{matrix} \right.\ \Rightarrow H(3;2)\)
Đườn thẳng MI vuông góc với AB nên ta có phương trình \(x + y - 3 = 0\)
Tọa độ điểm M là nghiệm của hệ phương trình:
\(\Leftrightarrow \left\{ \begin{matrix}
x + y - 3 = 0 \\
x - y + 1 = 0 \\
\end{matrix} \right.\ \Leftrightarrow \left\{ \begin{matrix}
x = 1 \\
x = 2 \\
\end{matrix} \right.\ \Rightarrow M(1;2)\)
\(\overrightarrow{HC} =
2\overrightarrow{MI} \Leftrightarrow \left\{ \begin{matrix}
x_{C} - x_{H} = 2\left( x_{I} - x_{M} \right) \\
y_{C} - y_{H} = 2\left( y_{I} - y_{M} \right) \\
\end{matrix} \right.\)
\(\Leftrightarrow \left\{ \begin{matrix}
x_{C} - 3 = 2(2 - 1) \\
y_{C} - 2 = 2(1 - 2) \\
\end{matrix} \right.\ \Leftrightarrow \left\{ \begin{matrix}
x_{C} = 5 \\
y_{C} = 0 \\
\end{matrix} \right.\ \Rightarrow C(5;0)\)
Ví dụ: Trong mặt phẳng \(Oxy\) cho các điểm \(A(6;2),B( - 2;8),C( - 2; -
4)\). Viết phương trình đường tròn nội tiếp tam giác \(ABC\)?
Hướng dẫn giải
Có \(AB = \sqrt{(6 + 2)^{2} + (2 - 8)^{2}}
= 10,AC = \sqrt{(6 + 2)^{2} + (2 + 4)^{2}} = 10\), tam giác \(ABC\) cân tại \(A\).
Gọi \(M = ( - 2;2)\) là trung điểm của \(BC\).
Phương trình \(AM\) là: \(y =
2\).
Phương trình \(BC:x = - 2\), phương trình \(AB\) :
\(\frac{x - 6}{6 + 2} = \frac{y - 2}{2 -
8} \Leftrightarrow 3x + 4y - 26 = 0\)
Gọi \(I = (x,y)\) là tâm đường tròn nội tiếp tam giác \(ABC\). Ta có:
\(\left. \ d(I,BC) = d(I,AB) \right.\)
\(\Leftrightarrow \frac{|x + 2|}{\sqrt{1^{2} + 0^{2}}} = \frac{|3x + 4y -
26|}{\sqrt{3^{2} + 4^{2}}}\)
\(\Leftrightarrow |3x + 4y - 26| = 5|x + 2|
\Leftrightarrow\)\(|\ \begin{matrix}
4x + 2y - 8 = 0 \\
x - 2y + 18 = 0 \\
\end{matrix}\)
Thay tọa độ của \(A\) và \(C\) vào phương trình \(4x + 2y - 8 = 0\) và xét tích của chúng, ta được:
:\((4.6 + 2.2 - 8)(4.( - 2) + 2.( - 4) - 8)
< 0\) nên phương trình \(BI\) là \(4x + 2y - 8 = 0\).
Tọa độ của \(I\) là nghiệm của hệ \(\left\{ \begin{matrix}
y = 2 \\
4x + 2y - 8 = 0 \\
\end{matrix} \Leftrightarrow \left\{ \begin{matrix}
x = 1 \\
y = 2 \\
\end{matrix} \right.\ \right.\).
Vậy \(I = (1;2)\)\(IM = \sqrt{(1 + 2)^{2} + (2 - 2)^{2}} =
3\).
Phương trình đường tròn nội tiếp tam giác \(ABC\) là \((x -
1)^{2} + (y - 2)^{2} = 9\).
---------------------------------------------
Qua việc tìm hiểu tâm đường tròn nội tiếp tam giác, có thể thấy đây không chỉ là một khái niệm hình học cơ bản mà còn là nền tảng quan trọng để giải quyết nhiều bài toán liên quan đến đường phân giác, khoảng cách từ điểm đến cạnh và diện tích tam giác. Khi nắm vững cách xác định tâm nội tiếp, học sinh sẽ dễ dàng nhận diện mối liên hệ giữa các yếu tố hình học và vận dụng linh hoạt vào từng dạng bài cụ thể.
Đặc biệt, trong chương trình Toán 10, kiến thức về đường tròn nội tiếp tam giác thường xuất hiện dưới nhiều hình thức khác nhau, từ chứng minh hình học đến bài toán tính toán. Việc hiểu rõ bản chất và tính chất của tâm nội tiếp sẽ giúp người học tránh được những sai lầm thường gặp, đồng thời nâng cao khả năng suy luận và trình bày lời giải mạch lạc.
Hy vọng bài viết đã cung cấp cho bạn cái nhìn đầy đủ và dễ hiểu về tâm đường tròn nội tiếp tam giác, giúp việc học hình học trở nên nhẹ nhàng và hiệu quả hơn. Đừng quên luyện tập thêm các bài toán vận dụng để củng cố kiến thức và sẵn sàng cho các dạng bài nâng cao cũng như các kỳ kiểm tra quan trọng.
