Cách phát hiện số liệu bất thường hoặc không chính xác của mẫu số liệu không ghép nhóm
Cách phát hiện số liệu bất thường trong mẫu số liệu
Trong quá trình thống kê, việc xử lý mẫu số liệu không ghép nhóm đòi hỏi sự chính xác cao. Tuy nhiên, thực tế cho thấy trong nhiều bộ dữ liệu thường tồn tại những số liệu bất thường hoặc không chính xác, gây ảnh hưởng đến kết quả phân tích. Ở Toán 10 – Chuyên đề Mẫu số liệu không ghép nhóm, học sinh được trang bị phương pháp để phát hiện và loại bỏ số liệu bất hợp lý, từ đó nâng cao độ tin cậy của kết quả thống kê. Bài viết này sẽ hướng dẫn chi tiết cách phát hiện số liệu bất thường hoặc sai lệch trong mẫu số liệu, kèm theo ví dụ minh họa dễ hiểu để bạn nắm vững và áp dụng hiệu quả.
Thế nào là giá trị bất thường?
Trong mẫu số liệu thống kê, có khi gặp những giá trị quá lớn hoặc quá nhỏ so với đa số các giá trị khác. Những giá trị này được gọi là giá trị bất thường. Chúng xuất hiện trong mẫu số liệu có thể do nhầm lẫn hay sai sót nào đó. Ta có thể dùng biểu đồ hộp để phát hiện những giá trị bất thường này.
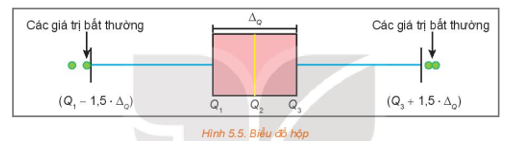
Các giá trị lớn hơn 
\(Q_{3} +
1,5.\Delta_{Q}\) hoặc bé hơn \(Q_{1} -
1,5.\Delta_{Q}\) được xem là giá trị bất thường.
Ví dụ minh họa xác định giá trị bất thường
Ví dụ 1: Hàm lượng Natri (đơn vị mg) trong 100 g một số loại ngũ cốc được cho như sau:
| 0 | 340 | 70 | 140 | 200 | 180 | 210 | 150 | 100 | 130 |
| 140 | 180 | 190 | 160 | 290 | 50 | 220 | 180 | 200 | 210 |
Tìm giá trị bất thường trong mẫu số liệu trên bằng cách sử dụng biểu đồ hộp.
Hướng dẫn giải
Từ mẫu số liệu ta tính được \(Q_{1} =
135\) và \(Q_{3} = 205\). Do đó, khoảng tứ phân vị là:
\(\Delta_{Q} = 205 - 135 = 70\)
Biểu đồ hộp cho mẫu số liệu này là:
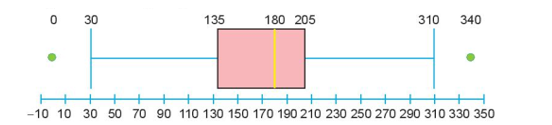
Ta có \(Q_{1} - 1,5.\Delta_{Q} =
30\) và \(Q_{3} + 1,5.\Delta_{Q} =
310\) nên trong mẫu số liệu có hai giá trị được xem là bất thường là 340 mg (lớn hơn 310 mg) và 0 mg (bé hơn 30 mg).
Ví dụ 2: Kết quả điều tra mức lương hằng tháng của \(8\) công nhân của nhà máy A được cho ở mẫu số liệu sau (đơn vị: triệu đồng): \(4\ \ \ \ \
5\ \ \ \ \ 5\ \ \ \ \ 47\ \ \ \ 5\ \ \ \ 6\ \ \ \ \ 4\ \ \ \ \
4\)
Giá trị ngoại lệ trong mỗi mẫu số liệu trên là:
A. \(47.\) B. \(4.\) C. \(5.\) D. Không có giá trị ngoại lệ
Hướng dẫn giải
Chọn A
+ Sắp xếp các số liệu theo thứ tự không giảm, ta được:
4; 4; 4; 5; 5; 5; 6; 47.
Vì cỡ mẫu là 8 là số chẵn nên tứ phân vị thứ hai là Q2 = 5.
Tứ phân vị thứ nhất là trung vị của mẫu: 4; 4; 4; 5. Do đó Q1 = 4.
Tứ phân vị thứ ba là trung vị của mẫu: 5; 5; 6; 47. Do đó Q3 = 5,5.
+ Khoảng tứ phân vị của mẫu số liệu ở nhà máy A là: ∆QA = 5,5 – 4 = 1,5.
Ta có: Q3A + 1,5∆QA = 5,5 + 1,5 . 1,5 = 7,75 và Q1A – 1,5∆QA = 4 – 1,5 . 1,5 = 1,75.
Do đó giá trị ngoại lệ trong mẫu số liệu ở nhà máy A là 47.
Ví dụ 3. Kết quả điều tra mức lương hằng tháng của \(9\) công nhân của một nhà máy được cho ở mẫu số liệu sau (đơn vị: triệu đồng): \(2\ \ \
\ \ 9\ \ \ \ \ 9\ \ \ \ \ 8\ \ \ \ 10\ \ \ 9\ \ \ \ \ 9\ \ \ \ 11\ \ \ \
\ 9\). Tìm giá trị ngoại lệ trong mỗi mẫu số liệu đó?
Hướng dẫn giải
+ Sắp xếp các số liệu theo thứ tự không giảm, ta được:
\(2;\ 8;\ 9;\ 9;\ 9;\ 9;\ 9;\ 10;\
11.\)
Vì cỡ mẫu là 9 là số lẻ nên tứ phân vị thứ hai là Q2 = 9.
Tứ phân vị thứ nhất là trung vị của mẫu: \(2;\ 8;\ 9;\ 9\). Do đó Q1 = 8,5.
Tứ phân vị thứ ba là trung vị của mẫu: \(9;\ 9;\ 10;\ 11.\)Do đó Q3 = 9,5.
+ Khoảng tứ phân vị của mẫu số liệu ở nhà máy là: ∆ = 9,5 – 8,5 = 1.
Ta có: Q3 + 1,5∆= 9,5 + 1,5 . 1 = 11 và Q1 – 1,5∆ = 8,5 – 1,5 . 1 = 7.
Do đó giá trị ngoại lệ trong mẫu số liệu ở nhà máy là 2.
Ví dụ 4. Bạn A cân lần lượt \(50\)quả vải thiều được lựa chọn ngẫu nhiên từ vườn nhà mình và được kết quả như sau:
|
Cân nặng (đơn vị gam) |
Số quả |
|
8 |
1 |
|
19 |
10 |
|
20 |
19 |
|
21 |
17 |
|
22 |
3 |
Tìm giá trị ngoại lệ của mẫu số liệu trên?
Hướng dẫn giải
Tứ phân vị thứ hai là trung vị của mẫu số liệu đã cho nên Q2 = 20.
Tứ phân vị thứ nhất là trung vị của mẫu: 8; 19; 19; 19; 19; 19; 19; 19; 19; 19; 19; 20; 20; 20; 20; 20; 20; 20; 20; 20; 20; 20; 20; 20; 20. Do đó Q1 = 20.
Tứ phân vị thứ ba là trung vị của mẫu: 20; 20; 20; 20; 20; 21; 21; 21; 21; 21; 21; 21; 21; 21; 21; 21; 21; 21; 21; 21; 21; 21; 22; 22; 22. Do đó Q3 = 21.
Khoảng tứ phân vị là ∆Q = 21 – 20 = 1.
Ta có: Q3 + 1,5∆Q = 21 + 1,5 . 1 = 22,5 và Q1 – 1,5∆Q = 20 – 1,5 . 1 = 18,5.
Do đó giá trị ngoại lệ của mẫu số liệu đã cho là 8.
---------------------------------------------------------
Như vậy, qua bài viết, bạn đã được tìm hiểu rõ ràng về cách nhận diện số liệu bất thường hoặc không chính xác trong mẫu số liệu không ghép nhóm. Đây là kỹ năng quan trọng trong phân tích thống kê, giúp đảm bảo kết quả tính toán phản ánh đúng bản chất dữ liệu. Việc thành thạo kỹ năng này không chỉ hữu ích trong học tập Toán 10 mà còn mang lại giá trị ứng dụng cao trong thực tế khi làm việc với dữ liệu. Hãy luyện tập thêm nhiều ví dụ khác để củng cố kiến thức và tự tin khi giải các dạng bài tập thống kê.
