Tìm m để hàm số có tập xác định R
Tìm tham số m để hàm số có tập xác định R
Trong chương trình Toán 10, dạng bài Tìm m để hàm số có tập xác định R thường xuất hiện trong các bài kiểm tra và đề thi vì giúp học sinh nắm vững bản chất hàm số, điều kiện xác định và khả năng phân tích tham số. Bài viết này cung cấp phương pháp tổng quát, các dạng bài phổ biến, kèm đáp án chi tiết giúp bạn hiểu rõ khi nào hàm số xác định trên toàn bộ tập số thực và cách xử lý từng trường hợp liên quan đến căn thức, mẫu số, biểu thức lôgarit, phân thức có tham số m.
A. Cách tìm tham số m để hàm số xác định trên tập số thực
Bài toán tổng quát. Cho hàm 
\(y =
f(x,m)\). Tìm tất cả các giá trị của \(m\) để hàm số xác định trên tập \(K\).
-
Bước 1: Tìm điều kiện xác định của hàm số (theo
\(m\)). Gọi D là tập xác định của hàm số. -
Bước 2: Hàm số xác định trên tập
\(K\) khi và chỉ khi \(K \subset D\).
Một số lưu ý:
+ Hàm số \(y = \frac{A}{f(x,m)}\) (\(A\)là biểu thức luôn có nghĩa) xác định trên tập \(K\) khi và chỉ khi phương trình \(f(x,m) = 0\) vô nghiệm trên \(K\).
+ Hàm số \(y = \sqrt{f(x,m)}\) xác định trên tập \(K\) khi và chỉ khi bất phương trình \(f(x,m) \geq 0\) nghiệm đúng với mọi \(x \in K\).
+ Hàm số \(y =
\frac{A}{\sqrt{f(x,m)}}\) (\(A\)là biểu thức luôn có nghĩa) xác định trên tập \(K\) khi và chỉ khi bất phương trình \(f(x,m) > 0\) nghiệm đúng với mọi \(x \in K\).
+ \(K \subset \left( D_{1} \cap D_{2}
\right) \Leftrightarrow \left\{ \begin{matrix}
K \subset D_{1} \\
K \subset D_{2}
\end{matrix} \right.\)
B. Bài tập minh họa tìm tham số m để hàm số xác định trên R
Ví dụ 1. Có bao nhiêu giá trị nguyên của tham số \(m\) để hàm số \(y
= \frac{2024x + 2025}{\sqrt{mx^{2} + 2mx + 9}}\) có tập xác định \(\mathbb{R}\) ?
Hướng dẫn giải
Hàm số \(y = \frac{2024x +
2025}{\sqrt{mx^{2} + 2mx + 9}}\) có tập xác định \(\mathbb{R}\) \(\Leftrightarrow mx^{2} + 2mx + 9 > 0,\forall x
\in \mathbb{R}^{}(1)\).
+ \(m = 0\) thoả mãn \((1)\).
+ \(m \neq 0\), \((1) \Leftrightarrow\)parabol \(y = mx^{2} + 2mx + 9 > 0\) nằm hoàn toàn phía trên trục hoành
\(\Leftrightarrow \left\{
\begin{matrix}
m > 0 \\
- \frac{\Delta}{4m} > 0
\end{matrix} \right.\ \Leftrightarrow \left\{ \begin{matrix}
m > 0 \\
\Delta = m^{2} - 9m < 0
\end{matrix} \right.\ \Leftrightarrow 0 < m < 9\)
Kết hợp 2 trường hợp ta được \(\Leftrightarrow 0 \leq m < 9\).
Vậy có 9 giá trị nguyên của \(m\) thoả mãn.
Ví dụ 2. Tìm tất cả các giá trị nguyên của tham số m để hàm số \(y = \frac{2018x + 2019}{\sqrt{(m - 1)x^{2} + 2(m -
1)x + 4}}\) có tập xác định là \(\mathbb{R}\)?
Hướng dẫn giải
Hàm số có TXĐ là \(\mathbb{R}\) khi và chỉ khi
\(f(x) = (m - 1)x^{2} + 2(m - 1)x + 4 >
0,\ \ \forall x\mathbb{\in R}\)
Với m = 1, ta có f(x) = 4 > 0, mọi x thuộc \(\mathbb{R}\). Do đó m = 1 thỏa mãn
Với \(m \neq 1,\ \ f(x) > 0,\ \ \forall
x\mathbb{\in R \Leftrightarrow}\left\{ \begin{matrix}
m > 1 \\
(m - 1)^{2} - 4(m - 1) < 0
\end{matrix} \right.\)
\(\Leftrightarrow \left\{ \begin{matrix}
m > 1 \\
(m - 1)(m - 5) < 0
\end{matrix} \right.\ \Leftrightarrow \left\{ \begin{matrix}
m > 1 \\
1 < m < 5
\end{matrix} \right.\ \Leftrightarrow 1 < m < 5\)
Vậy có 4 số nguyên \(m \in \{
1,2,3,4\}\) thỏa mãn hàm số có TXĐ là \(\mathbb{R}\).
Ví dụ 3. Cho hàm số\(y = \sqrt{x^{4} +
4x^{3} + (m + 5)x^{2} + 4x + 4 + m}\). Tìm tất cả các giá trị của \(m\) để hàm số xác định trên \(\mathbb{R}\).
Hướng dẫn giải
Ta có \(x^{4} + 4x^{3} + (m + 5)x^{2} + 4x
+ 4 + m = \left( x^{2} + 1 \right)\left\lbrack (x + 2)^{2} + m
\right\rbrack\)
Điều kiện xác định của hàm số là:\((x +
2)^{2} + m \geq 0\)(*)
Hàm số xác định trên \(R
\Leftrightarrow\) (*) nghiệm đúng với mọi \(\forall x \in R\)
\(\Leftrightarrow (x + 2)^{2} \geq - m\ \
\forall x \in R\) \(\Leftrightarrow\) \(0 \geq - m \Leftrightarrow m \geq 0\).
C. Bài tập vận dụng có hướng dẫn chi tiết
Bài tập 1. Cho hàm số \(f(x)\) có đồ thị như hình vẽ.
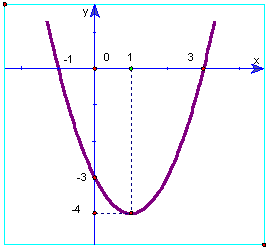
Tìm giá trị nguyên lớn nhất của \(m\) để hàm số \(y
= \frac{1}{\sqrt{f(x) - 2m + 2}}\)có TXĐ là \(\mathbb{R}\)?
Bài tập 2. Cho hàm sô \(y = \frac{2mx +
4}{\sqrt{x^{2} + 2mx + 2018m + 2019}} + \sqrt{mx^{2} + 2mx +
2020}\). Gọi S là tập hợp các giá trị nguyên của \(m\) để hàm số xác định trên \(\mathbb{R}\). Hỏi tập S có bao nhiêu phần tử?
Bài tập 3. Cho hàm số \(y = \sqrt{x^{4} -
x^{2} + 1 + mx\sqrt{2x^{4} + 2}}\). Tìm tất cả các giá trị của tham số m để hàm số có tập xác định là tập số thực \(\mathbb{R}.\)
Tài liệu quá dài để hiển thị hết — hãy nhấn Tải về để xem trọn bộ!
-------------------------------------------
Qua hệ thống ví dụ có lời giải và các bước phân tích điều kiện xác định theo từng dạng, bạn đã có thể tự tin giải bất kỳ bài tập nào yêu cầu tìm m để hàm số có tập xác định R. Đây là nền tảng quan trọng giúp bạn học tốt hơn các chương tiếp theo như khảo sát hàm số, tính đạo hàm hay giải phương trình – bất phương trình chứa tham số.
Hãy tiếp tục luyện tập với các bài tập mở rộng để nâng cao tư duy và tăng tốc độ xử lý dạng toán tham số trong Toán 10.
