Cho tam giác đều với đường cao
. Đẳng thức nào sau đây đúng.
Đáp án “” sai do hai vectơ ngược hướng.
Đáp án “” đúng vì
là trung điểm
và
cùng hướng .
Trong chương Vectơ Toán 10, kiến thức về hai vectơ bằng nhau là nền tảng quan trọng giúp học sinh hiểu rõ bản chất phương, hướng và độ dài của vectơ. Việc nắm vững định nghĩa, tính chất và dấu hiệu nhận biết hai vectơ bằng nhau giúp học sinh giải nhanh các dạng bài hình học phẳng, bài toán tọa độ và các bài kiểm tra trắc nghiệm một cách chính xác.
Bài viết dưới đây tổng hợp bộ câu hỏi trắc nghiệm Toán 10 về hai vectơ bằng nhau có đáp án và lời giải chi tiết, giúp các em ôn tập lý thuyết, luyện tập kỹ năng và củng cố kiến thức Vectơ Toán 10 hiệu quả nhất.
Cho tam giác đều với đường cao
. Đẳng thức nào sau đây đúng.
Đáp án “” sai do hai vectơ ngược hướng.
Đáp án “” đúng vì
là trung điểm
và
cùng hướng .
Cho tứ giác . Điều kiện nào là điều kiện cần và đủ để
?
Ta có:
• là hình bình hành.
• Mặt khác, là hình bình hành
.
Do đó, điều kiện cần và đủ để là
là hình bình hành.
Gọi lần lượt là trung điểm của các cạnh
của tam giác đều
. Đẳng thức nào sau đây đúng?
Hình vẽ minh họa:
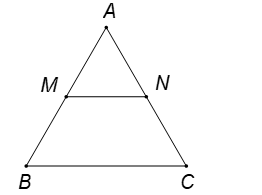
Ta có là đường trung bình của tam giác
.
Do đó
Cho hình bình hành . Đẳng thức nào sau đây sai.
Ta có: sai do
là hình bình hành.
Chọn câu sai?
Đáp án sai là: vì
.
Cho lục giác đều tâm
. Ba vectơ bằng vecto
là:
Hình vẽ minh họa:
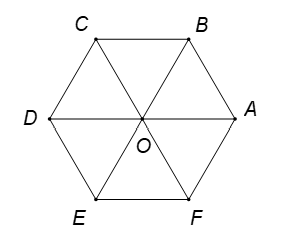
Ba vectơ bằng vecto là
.
Cho hình bình hành . Đẳng thức nào sau đây đúng.
Ta có:
Hình bình hành .
Cho lục giác đều có tâm
. Đẳng thức nào sau đây là sai?
Hình vẽ minh họa
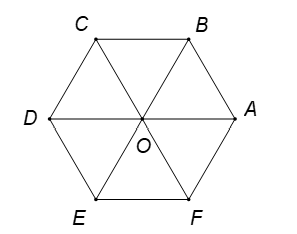
Hai vectơ cùng phương nhưng ngược hướng nên
Đẳng thức sai là:
Cho tam giác có trực tâm
. Gọi
là điểm đối xứng với
qua tâm
của đường tròn ngoại tiếp tam giác
. Khẳng định nào sau đây là đúng?
Hình vẽ minh họa:
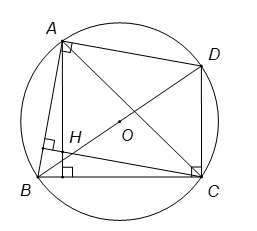
Ta có và
(do góc
chắn nửa đường tròn).
Suy ra
Tương tự ta cũng có
Suy ra tứ giác là hình bình hành.
Do đó và
.
Hai vectơ được gọi là bằng nhau khi và chỉ khi
Hai vectơ được gọi là bằng nhau khi và chỉ khi chúng cùng hướng và độ dài của chúng bằng nhau.
Cho tứ giác . Gọi
lần lượt là trung điểm của
. Trong các khẳng định sau, hãy tìm khẳng định sai?
Ta có là đường trung bình của tam giác
.
Suy ra: hay
.
Vậy đáp án sai là:
Cho hình bình hành . Trong các khẳng định sau hãy tìm khẳng định sai?
Hình vẽ minh họa
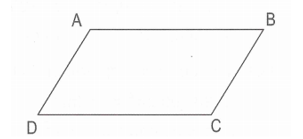
Ta có là hình bình hành. Suy ra:
.
Vậy đáp án sai là:
Cho lục giác , tâm
. Trong các khẳng định dưới đây, có bao nhiêu khẳng định đúng?
i) . ii)
. iii)
.
Hình vẽ minh họa:
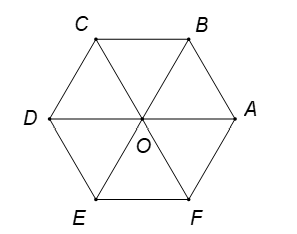
Ta có là lục giác, tâm
. Suy ra
,
,
.
Cho hình vuông , khẳng định nào sau đây đúng?
Ta có là hình vuông. Suy ra:
.
Vậy khẳng định đúng là: .
Cho lục giác đều tâm
. Số các vectơ bằng
có điểm đầu và điểm cuối là các đỉnh của lục giác là:
Hình vẽ minh họa:
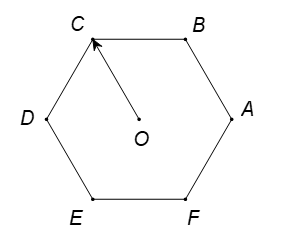
Đó là các vectơ: . Vậy có 2 vectơ có điểm đầu và điểm cuối là các đỉnh của lục giác và bằng
.
Cho tứ giác Gọi
lần lượt là trung điểm của
Khẳng định nào sau đây là sai?
Hình vẽ minh họa:
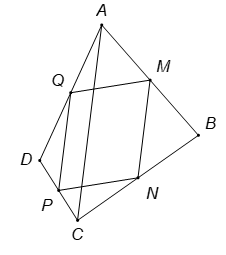
Ta có (do cùng song song và bằng
).
Do đó là hình bình hành.
Cho tam giác đều . Mệnh đề nào sau đây là sai?
Đáp án “” sai do hai vectơ không cùng phương.
Cho tam giác đều . Mệnh đề nào sau đây sai?
Ta có: Tam giác đều
không cùng hướng
.
Cho và một điểm
. Có bao nhiêu điểm
thỏa mãn
?
Ta có .
Suy ra tập hợp các điểm thỏa yêu cầu bài toán là đường tròn tâm
bán kính
.
Gọi là giao điểm của hai đường chéo của hình bình hành
. Đẳng thức nào sau đây sai?
Đẳng thức sai là:
Cho tứ giác . Nếu
thì
là hình gì? Tìm đáp án sai.
Nếu thì
là hình thang.
Gọi là giao điểm của hai đường chéo hình chữ nhật
. Mệnh đề nào sau đây đúng?
Mệnh đề đúng là:
Cho khẳng định sau
(1). điểm
,
,
,
là
đỉnh của hình bình hành thì
.
(2). điểm
,
,
,
là
đỉnh của hình bình hành thì
.
(3). Nếu thì
điểm
là
đỉnh của hình bình hành.
(4). Nếu thì
điểm
,
,
,
theo thứ tự đó là
đỉnh của hình bình hành.
Hỏi có bao nhiêu khẳng định sai?
Nếu thì
điểm
,
,
,
theo thứ tự đó là
đỉnh của hình bình hành.
Vậy có hai khẳng định sai.
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây: