Tam giác có
. Gọi
là độ dài ba đường trung tuyến,
trọng tâm. Xét các khẳng định sau:
.
.
.
.
Trong các khẳng định đã cho có
Ta có:
.
Phần Hệ thức lượng trong tam giác là một chuyên đề trọng tâm trong chương trình Toán 10, giúp học sinh vận dụng linh hoạt các công thức lượng giác để giải các bài toán hình học phức tạp. Bài viết này tổng hợp trắc nghiệm Hệ thức lượng trong tam giác (mức vận dụng – vận dụng cao) kèm đáp án chi tiết, giúp bạn rèn luyện kỹ năng tư duy, phân tích và giải quyết các bài toán nâng cao. Bộ bài tập Toán 10 Hệ thức lượng có đáp án này được biên soạn bám sát cấu trúc đề thi, giúp học sinh củng cố kiến thức, tăng tốc ôn luyện và đạt điểm cao trong các kỳ kiểm tra.
Tam giác có
. Gọi
là độ dài ba đường trung tuyến,
trọng tâm. Xét các khẳng định sau:
.
.
.
.
Trong các khẳng định đã cho có
Ta có:
.
Tam giác có hai đường trung tuyến
vuông góc với nhau và có
, góc
. Tính diện tích tam giác
.
Vì . (Áp dụng hệ quả đã có trước)
Trong tam giác , ta có
Khi đó .
Cho hình bình hành có
và
. Trong các biểu thức sau, biểu thức nào đúng:
Gọi là giao điểm của
và
Ta có:
là trung tuyến của tam giác
.
Tam giác ABC có trọng tâm . Hai trung tuyến
,
và
. Tính độ dài cạnh
.
Hình vẽ minh họa:
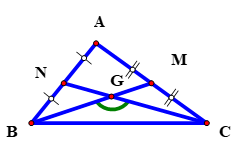
Ta có: và
là hai góc kề bù mà
là trọng tâm của tam giác
Trong tam giác ta có:
là trung điểm của
Tam giác có
và độ dài đường cao
. Tính độ dài cạnh
.
Ta có:
.
=> .
Mặt khác:
Từ đó ta có:
Tam giác vuông tại
có đường cao
và
. Tính bán kính
của đường tròn ngoại tiếp tam giác
.
Tam giác vuông tại
có đường cao
Mặt khác thế vào
ta được
Suy ra
Vậy bán kính cần tìm là
Tam giác vuông tại
có
cm. Hai đường trung tuyến
và
cắt nhau tại
. Diện tích tam giác
bằng:
Vì là trung điểm của
Đường thẳng cắt
tại
suy ra
là trọng tâm tam giác
Khi đó
Vậy diện tích tam giác là:
Tam giác có độ dài ba trung tuyến lần lượt là
. Diện tích của tam giác
bằng:
Ta có:
Ta có:
Diện tích tam giác
Tam giác đều nội tiếp đường tròn bán kính cm có diện tích bằng:
Xét tam giác đều, có độ dài cạnh bằng
Theo định lí sin, ta có
Vậy diện tích cần tính là:
.
Tam giác có
. Các cạnh
liên hệ với nhau bởi đẳng thức
. Góc giữa hai trung tuyến
và
là góc nào?
Gọi là trọng tâm tam giác
Ta có:
Trong tam giác ta có:
Tam giác vuông cân tại
và nội tiếp trong đường tròn tâm
bán kính
. Gọi
là bán kính đường tròn nội tiếp tam giác
. Khi đó tỉ số
bằng:
Giả sử .
Suy ra .
Ta có:
.
Diện tích tam giác vuông .
Lại có
Vậy .
Tam giác có
và có diện tích
. Nếu tăng cạnh
lên
lần đồng thời tăng cạnh
lên
lần và giữ nguyên độ lớn của góc
thì khi đó diện tích của tam giác mới được tạo nên bằng:
Diện tích tam giác ban đầu là:
Khi tăng cạnh lên
lần và cạnh
lên
lần thì diện tích tam giác
lúc này là
Cho tam giác có
. Nếu giữa
có liên hệ
thì độ dài đường trung tuyến xuất phát từ đỉnh
của tam giác tính theo
bằng:
Hệ thức trung tuyến xuất phát từ đỉnh của tam giác:
Mà:
Cho tam giác có
và
. Gọi
là trung điểm
. Tính bán kính
của đường tròn ngoại tiếp tam giác
Vì là trung điểm của
Tam giác có
Tam giác
đều.
Nên có bán kính đường tròn ngoại tiếp là:
Tam giác có ba đường trung tuyến
thỏa mãn
. Khi đó tam giác này là tam giác gì?
Ta có:
Mà:
Tam giác
vuông.
Tam giác có
. Gọi
là trung điểm của
. Biết
và
. Tính độ dài cạnh
.
Hình vẽ minh họa:
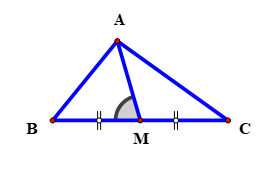
Trong tam giác ta có:
Ta có: và
là hai góc kề bù.
Trong tam giác ta có:
.
Tam giác có
và
. Tam giác
có diện tích lớn nhất khi góc
bằng:
Diện tích tam giác là
Vì không đổi và
nên suy ra
Dấu "=" xảy ra khi và chỉ khi
Vậy giá trị lớn nhất của diện tích tam giác là
Tam giác nhọn có
,
là đường cao kẻ từ
và
. Bán kính đường tròn ngoại tiếp
của tam giác
được tính theo
và
là:
Xét tam giác vuông tại
có
Mà
và
Tam giác vuông tại
có:
Bán kính đường tròn ngoại tiếp cần tính là
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây: