Cho hình bình hành có
là trung điểm của
Khẳng định nào sau đây đúng?
Vì là hình bình hành nên
Và là trung điểm
nên
suy ra
Bài viết Trắc nghiệm Toán 10 Tích của một vectơ với một số (mức độ vận dụng) giúp học sinh rèn luyện kỹ năng thực hành và tư duy vận dụng trong giải toán vectơ. Với hệ thống bài tập Toán 10 vectơ có đáp án chi tiết, nội dung này hỗ trợ người học nắm chắc quy tắc nhân vectơ với số, đồng thời biết áp dụng vào các dạng bài phức tạp trong đề thi THPT Quốc gia.
Cho hình bình hành có
là trung điểm của
Khẳng định nào sau đây đúng?
Vì là hình bình hành nên
Và là trung điểm
nên
suy ra
Cho tam giác đều cạnh
Biết rằng tập hợp các điểm
thỏa mãn đẳng thức
là đường tròn cố định có bán kính
Tính bán kính
theo
Gọi là trọng tâm của tam giác
Ta có
Chọn điểm sao cho
Mà là trọng tâm của tam giác
Khi đó
Do đó
Vì là điểm cố định thỏa mãn
nên tập hợp các điểm
cần tìm là đường tròn tâm
bán kính
Cho hình thang có đáy là
và
Gọi
và
lần lượt là trung điểm của
và
Khẳng định nào sau đây sai ?
Hình vẽ minh họa:
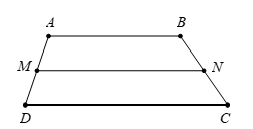
Vì lần lượt là trung điểm của
Dựa vào đáp án, ta có nhận xét sau:
Đáp án đúng
VVì
Đáp án đúng, vì
Đáp án đúng, vì
và
Suy ra
Đáp án sai, vì theo phân tích ở đáp án
.
Cho tam giác đều cạnh
trọng tâm
Tìm tập hợp các điểm
thỏa mãn
Gọi lần lượt là trung điểm của
Khi đó
Theo bài ra, ta có
Vậy tập hợp các điểm thỏa mãn
là đường trung trực của đoạn thẳng
cũng chính là đường trung trực của đoạn thẳng
vì
là đường trung bình của tam giác
Cho tam giác vuông cân tại
cạnh
Tính
Hình vẽ minh họa
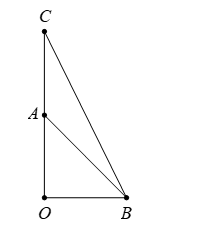
Gọi là điểm đối xứng của
qua
Tam giác vuông tại
có
Ta có:
suy ra
Cho tam giác , gọi
là trung điểm
và
là một điểm trên cạnh
sao cho
. Gọi
là trung điểm của
. Khi đó:
Ta có:
.
Cho hình chữ nhật và số thực
Tìm tập hợp các điểm
thỏa mãn đẳng thức
Gọi là tâm của hình chữ nhật
ta có
Do đó
Vì là điểm cố định nên tập hợp các điểm
thỏa mãn đẳng thức
là đường
tròn tâm bán kính
Cho tam giác và một điểm
tùy ý. Hãy chọn hệ thức đúng:
Ta có:
Cho tam giác đều và điểm
thỏa mãn
Mệnh đề nào sau đây đúng ?
Từ giả thiết là trung điểm của
Lại có
Cho tam giác điểm
thuộc cạnh
sao cho
và
là trung điểm của
Tính
theo
và
Vì là trung điểm
nên
Suy ra
Cho hai điểm phân biệt và cố định, với
là trung điểm của
Tìm tập hợp các điểm
thỏa mãn đẳng thức
Chọn điểm thuộc đoạn
sao cho
Chọn điểm thuộc đoạn
sao cho
Ta có
Vì là hai điểm cố định nên từ đẳng thức
suy ra tập hợp các điểm
là trung trực của đoạn thẳng
Gọi là trung điểm của
suy ra
cũng là trung điểm của
lời g
Vậy tập hợp các điểm thỏa mãn
là đường trung trực của đoạn thẳng
Cho tam giác có
là trung điểm của
Tính
theo
và
Ta có:
Cho hình chữ nhật và
là giao điểm của hai đường chéo. Tìm tập hợp các điểm
thỏa mãn
Gọi lần lượt là trung điểm của
Khi đó
Do đó
Vì là hai điểm cố định nên từ đẳng thức
tập hợp các điểm
là trung
trực của đoạn thằng hay chính là trung trực của đoạn thẳng
Cho tam giác có
là trung điểm của
là trọng tâm của tam giác
Khẳng định nào sau đây đúng ?
Hình vẽ minh họa:
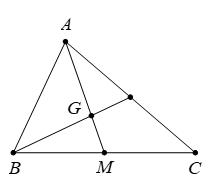
Vì là trọng tâm của tam giác
Và là trung điểm của
Do đó
Cho tam giác có
là trọng tâm. Trong các mệnh đề sau, tìm mệnh đề đúng?
Gọi là trung điểm của
Mà là trọng tâm của tam giác
suy ra
Từ suy ra
Cho tứ giác trên cạnh
lấy lần lượt các điểm
sao cho
và
Tính vectơ
theo hai vectơ
Hình vẽ minh họa:
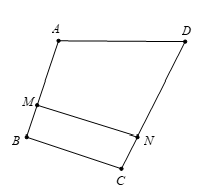
Ta có và
Suy ra
Theo bài ra, ta có và
Vậy
Cho hình bình hành Tính
theo
và
Vì là hình bình hành nên
Ta có và
Vậy
Cho ba điểm không thẳng hàng và điểm
thỏa mãn đẳng thức vectơ
Tính giá trị biểu thức
Do và
không cùng phương nên tồn tại các số thực
sao cho
Theo bài ra, ta có suy ra
Cho tam giác . Có bao nhiêu điểm
thỏa
?
Gọi là trọng tâm của tam giác
nên G cố định duy nhất và
.
Ta có
.
Vậy có vô số điểm thỏa mãn, với tập hợp
là đường tròn tâm
bán kính bằng
Cho tam giác vuông cân tại
cạnh
Khẳng định nào dưới đây là sai?
Dựa vào các đáp án, ta có nhận xét sau:
Đáp án “” đúng, gọi
nằm trên tia đối của tia
sao cho
Và nằm trên tia đối của tia
sao cho
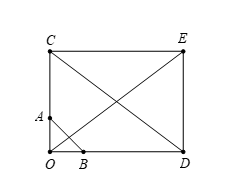
Dựng hình chữ nhật suy ra
(quy tắc hình bình hành).
Ta có
Đáp án “” đúng, vì
Đáp án “” sai, xử lý tương tự như ý đáp án
.
Đáp án “” đúng, vì
Cho tam giác có
là trung điểm của
là trung điểm của
Khẳng định nào sau đây đúng ?
Hình vẽ minh họa:
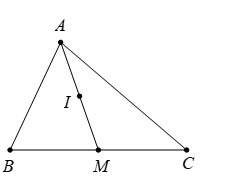
Vì là trung điểm
nên
Mặt khác là trung điểm
nên
Từ suy ra
Cho tam giác có
là trung điểm của
là trung điểm của
Khẳng định nào sau đây đúng?
Hình vẽ minh họa

Vì là trung điểm
nên
Mặt khác là trung điểm
nên
Suy ra
Cho tam giác hai điểm
chia cạnh
theo ba phần bằng nhau
Tính
theo
và
Ta có:
Cho hai điểm phân biệt và cố định, với
là trung điểm của
Tìm tập hợp các điểm
thỏa mãn đẳng thức
Vì là trung điểm của
suy ra
Do đó
Vậy tập hợp các điểm thỏa mãn đẳng thức
là đường tròn tâm
bán kính
Cho tam giác và điểm
thỏa mãn
Khẳng định nào sau đây đúng ?
Gọi lần lượt là trung điểm
và trọng tâm tam giác
Vì là trung điểm
nên
Theo bài ra, ta có suy ra
thẳng hàng
Mặt khác là trọng tâm của tam giác
Do đó, ba điểm thẳng hàng.
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây: