Cho tam giác vuông cân đỉnh
,
. Tính độ dài của
Hình vẽ minh họa

Ta có:
Gọi là trung điểm
Khi đó
Trắc nghiệm Toán 10 Tính độ dài vectơ là một phần quan trọng trong chuyên đề vectơ Toán học lớp 10, giúp học sinh làm quen với các bài toán cơ bản và nâng cao về cách tính độ dài của một vectơ trong không gian. Đây là kỹ năng cần thiết để giải quyết các bài toán liên quan đến ứng dụng vectơ trong nhiều tình huống thực tế. Bài viết này cung cấp các bài tập trắc nghiệm về tính độ dài vectơ, kèm theo đáp án chi tiết, giúp học sinh củng cố kiến thức và luyện tập hiệu quả.
Cho tam giác vuông cân đỉnh
,
. Tính độ dài của
Hình vẽ minh họa

Ta có:
Gọi là trung điểm
Khi đó
Cho tam giác vuông cân tại
có
. Tính
Hình vẽ minh họa
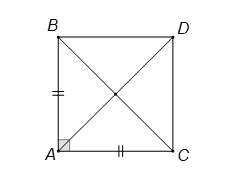
Gọi là điểm thỏa mãn tứ giác
là hình vuông.
Cho tam giác và điểm
thỏa mãn điều kiện
. Mệnh đề nào sau đây sai?
Hình vẽ minh họa :

Ta có :
là hình bình hành.
Cho hình vuông cạnh
. Tính
Ta có
Cho tam giác đều cạnh
. Khi đó
bằng:
Hình vẽ minh họa

Gọi là trung điểm của
Suy ra
Ta lại có .
Cho tam giác và điểm
thỏa mãn
. Tìm vị trí điểm
Hình vẽ minh họa:
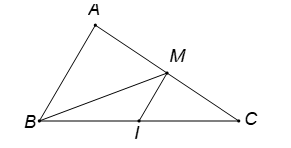
Gọi là trung điểm của
là trung điểm
Gọi là trọng tâm tam giác vuông
với cạnh huyền
. Tính độ dài của vectơ
.
Hình vẽ minh họa
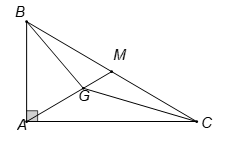
Gọi là trung điểm của
Ta có
Mà
Tam giác có
. Tính độ dài vectơ tổng
.
Hình vẽ minh họa:

Gọi là điểm thỏa mãn tứ giác
là hình thoi.
Ta có
là hình thoi có
và
là hai tam giác đều
Cho tam giác vuông tại
có
. Tính
.
Gọi là điểm thỏa mãn tứ giác
là hình chữ nhật.
Ta có :
.
Cho tam giác đều cạnh
,
là trung điểm của
. Tính
Hình vẽ minh họa

Gọi là điểm thỏa mãn tứ giác
là hình bình hành.
là hình chữ nhật.
Ta có:
Cho hình bình hành . Tập hợp các điểm
thỏa mãn
là?
Hình vẽ minh họa

Ta có:
sai
Không có điểm
thỏa mãn
Cho hình vuông cạnh
, tâm
. Tính
.
Hình vẽ minh họa:
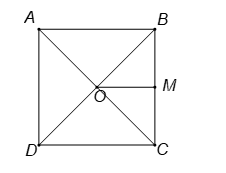
Gọi là trung điểm của
.
Cho tam giác có
thỏa mãn điều kiện
. Xác định vị trí điểm
Gọi là trọng tâm tam giác
.
Ta có : .
Cho tam giác Tập hợp các điểm
thỏa mãn đẳng thức:
là?
Ta có:
Mà cố định
Tập hợp điểm
là đường tròn tâm
, bán kính
.
Cho hình thoi có
. Tính
.
Hình vẽ minh họa
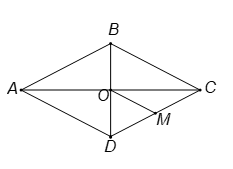
Gọi .
Gọi là trung điểm của
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây: