Trong chương Vectơ Toán 10, việc hiểu và vận dụng quy tắc tổng của hai vectơ là kỹ năng cơ bản giúp học sinh nắm chắc nền tảng kiến thức hình học phẳng và đại số vectơ. Ở mức độ nhận biết, học sinh cần phân biệt rõ vectơ cùng phương, quy tắc hình bình hành và quy tắc tam giác để tính tổng của hai vectơ một cách chính xác.
Bài viết dưới đây cung cấp bộ câu hỏi trắc nghiệm Toán 10 về tổng của hai vectơ (mức độ nhận biết) kèm đáp án chi tiết, giúp các em ôn tập lý thuyết nhanh, rèn kỹ năng tính toán và chuẩn bị tốt cho các bài kiểm tra trắc nghiệm Vectơ Toán 10.
Cho hình bình hành ,với giao điểm hai đường chéo là
. Khi đó:
Ta có: ,
,
.
Cho các điểm phân biệt . Đẳng thức nào sau đây đúng?
Ta có:
Điều kiện nào dưới đây là điều kiện cần và đủ để điểm là trung điểm của đoạn
.
Điều kiện cần và đủ để điểm O là trung điểm của đoạn AB là:
Chọn khẳng định đúng:
Khẳng định đúng là: “Nếu là trọng tâm tam giác
thì
.”
Cho 4 điểm bất kỳ . Đẳng thức nào sau đây là đúng:
Ta có: .
Chọn kết quả sai?
Ta có:
.
Vậy kết quả sai là: .
Cho hình bình hành có tâm
. Khẳng định nào sau đây là đúng:
Hình vẽ minh họa:
Ta có: .
Cho hình chữ nhật biết
và
thì độ dài
bằng bao nhiêu?
Ta có:
Cho bốn điểm phân biệt. Khi đó vectơ
bằng:
Ta có:
.
Cho hình bình hành tâm
. Khi đó
Ta có: .
Gọi là trung điểm của đoạn thẳng
. Đẳng thức nào sau đây là đúng?
Hình vẽ minh họa:
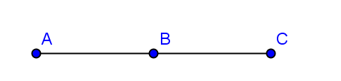
Do là trung điểm của đoạn thẳng
nên
.
Vectơ tổng bằng:
Ta có:
Cho các điểm phân biệt . Đẳng thức nào sau đây đúng?
Ta có:
.
Vậy khẳng định đúng cần tìm là: .
Cho hình bình hành với
là giao điểm của 2 đường chéo. Khẳng định nào sau đây là khẳng định sai?
Ta có: sai vì hai vectơ này không cùng phương.
Điều kiện nào sau đây không phải là điều kiện cần và đủ để là trọng tâm của tam giác
, với
là trung điểm của
.
Ta có: vì hai vectơ này không cùng phương.
Cho hình vuông có cạnh bằng
. Khi đó
bằng:
Ta có:
Kết quả bài toán tính là:
Ta có:
.
Cho 4 điểm bất kì. Chọn kết quả đúng
Ta có:
.
Chọn đẳng thức đúng:
Đẳng thức đúng là: .
Cho 4 điểm bất kì . Đẳng thức nào sau đây đúng?
Ta có:
.
Cho hình bình hành . Đẳng thức nào sau đây sai?
Ta có: . Vậy đẳng thức sai là:
.
Chọn khẳng định sai
Ta có:
.
Vậy khẳng định sai là: “Nếu là trung điểm đoạn
thì
.”
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:
