Cho hình vuông có cạnh bằng
. Khi đó
bằng:
Hình vẽ minh họa:
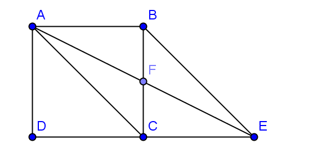
Dựng hình bình hành tâm
.
Ta có:
.
Trong chương trình Toán 10 – Chuyên đề Vectơ, việc hiểu và vận dụng tổng của hai vectơ ở mức độ thông hiểu giúp học sinh không chỉ nắm vững công thức, mà còn biết phân tích, suy luận và vận dụng linh hoạt quy tắc cộng vectơ trong các dạng bài nâng cao.
Bộ trắc nghiệm Toán 10 Tổng của hai vectơ (mức độ thông hiểu) dưới đây được biên soạn kèm đáp án chi tiết và hướng dẫn giải cụ thể, giúp học sinh ôn tập toàn diện, củng cố lý thuyết và luyện kỹ năng tư duy hình học – đại số vectơ hiệu quả nhất.
Cho hình vuông có cạnh bằng
. Khi đó
bằng:
Hình vẽ minh họa:

Dựng hình bình hành tâm
.
Ta có:
.
Cho tam giác đều cạnh
. Khi đó
có kết quả là:
Hình vẽ minh họa:
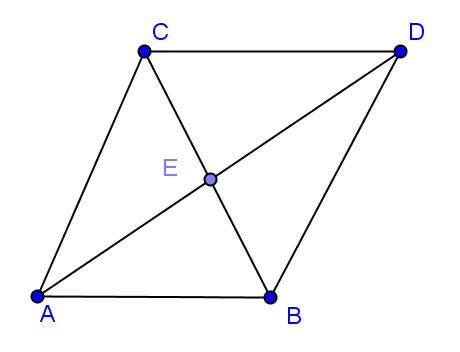
Dựng hình bình hành tâm
.
Ta có:
Cho hình vuông cạnh
, tâm
. Khi đó:
Hình vẽ minh họa:
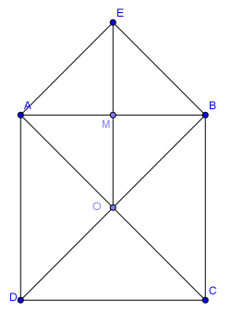
Dựng hình bình hành và gọi
là giao điểm của
và
.
Ta có:
Gọi là trọng tâm tam giác vuông
với cạnh huyền
. Tổng hai vectơ
có độ dài bằng bao nhiêu?
Dựng hình bình hành . Gọi
là trung điểm
.
Khi đó ta có
Cho tam giác đều có cạnh bằng
,
là trung điểm cạnh
. Vectơ
có độ dài là:
Hình vẽ minh họa:
Ta có: .
Cho hình thoi tâm
, cạnh bằng
và góc
bằng
. Kết luận nào sau đây đúng?
Hình vẽ minh họa:
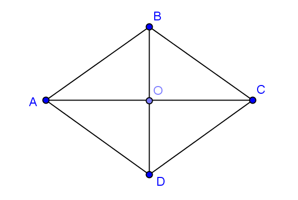
Do tam giác đều nên
Cho hình chữ nhật , gọi
là giao điểm của
và
, phát biểu nào là đúng?
Ta có:
.
Cho tam giác , trọng tâm là
. Phát biểu nào là đúng?
Ta có:
Cho hình bình hành tâm
. Đẳng thức nào sau đây đúng?
Ta có:
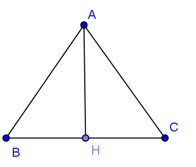
Cho vuông tại
và
,
. Vectơ
có độ dài bằng:
Hình vẽ minh họa:
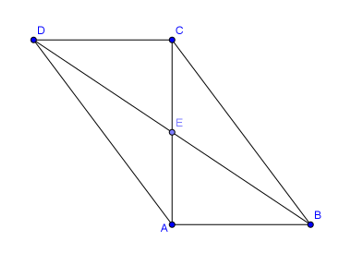
Dựng hình bình hành tâm
.
Ta có.
Cho các điểm phân biệt . Đẳng thức nào sau đây đúng?
Ta có: .
Cho là trọng tâm tam giác
vuông, cạnh huyền
. Độ dài vectơ
bằng:
Dựng hình bình hành . Gọi
là trung điểm
.
Khi đó ta có
Cho tam giác . Tập hợp những điểm
sao cho:
là:
Gọi lần lượt là trung điểm của
và
.
Khi đó:
Vậy nằm trên đường trung trực của
.
Cho tam giác đều cạnh
. Khi đó
Hình vẽ minh họa:
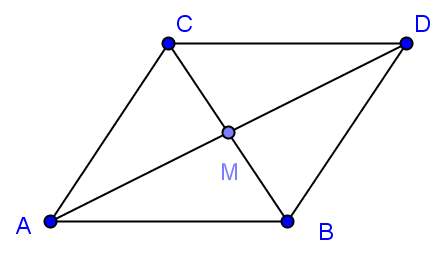
Dựng hình bình hành và gọi
là trung điểm của
.
Ta có
Cho 6 điểm . Đẳng thức nào sau đây đúng.
Ta có:
Cho lục giác đều và
là tâm của nó. Đẳng thức nào dưới đây là đẳng thức sai?
Hình vẽ minh họa:
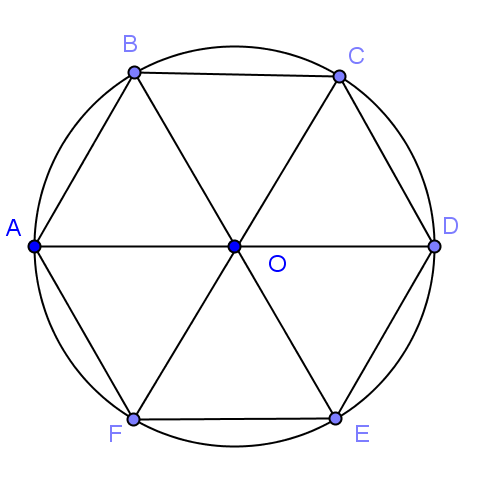
Ta có:
.
Cho tam giác đều cạnh
, trọng tâm là
. Phát biểu nào là đúng?
Hình vẽ minh họas
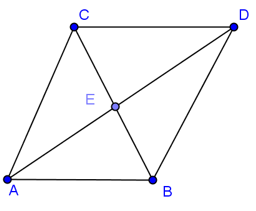
Dựng hình bình hành tâm
.
Ta có
Vậy .
Cho tam giác ABC. Gọi lần lượt là trung điểm các cạnh
. Hỏi
bằng vectơ nào?
Hình vẽ minh họa:
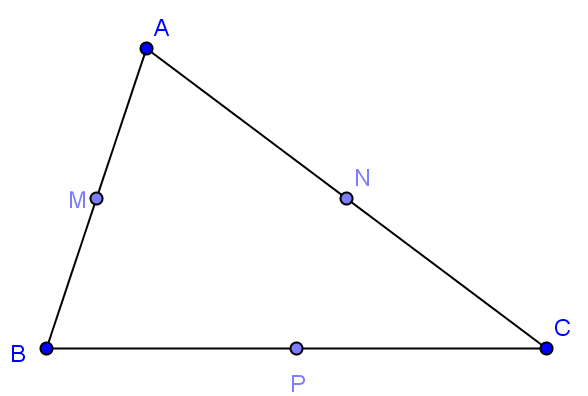
Theo qui tắc hình bình hành ta có .
Cho 4 điểm . Đẳng thức nào sau đây đúng.
Ta có:
.
Cho 4 điểm bất kỳ . Đẳng thức nào sau đây là đúng?
Ta có
.
Cho . Điểm
thỏa mãn
thì điểm
là
Ta có:
.
Vậy là đỉnh thứ tư của hình bình hành nhận
và
làm hai cạnh.
Cho tam giác . Để điểm
thoả mãn điều kiện
thì
phải thỏa mãn mệnh đề nào?
Ta có:
Vậy là điểm sao cho tứ giác
là hình bình hành.
Cho 6 điểm . Tổng vectơ:
bằng:
Ta có:
.
Cho hình thang có
song song với
. Cho
. Gọi
là trung điểm của
. Khi đó:
Hình vẽ minh họa:
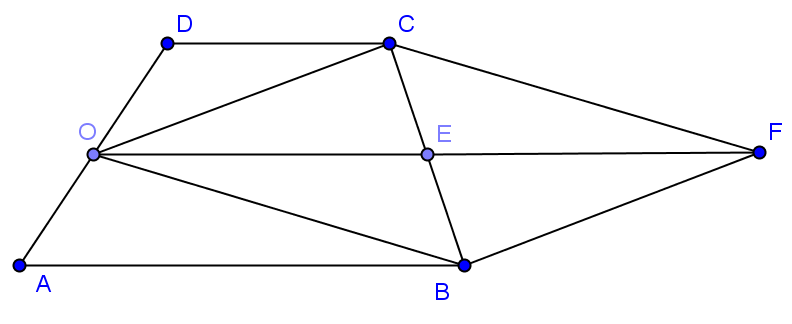
Dựng hình bình hành tâm
.
Khi đó:
.
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây: