VnDoc.com

Biểu diễn một vectơ thành hai vectơ không cùng phương

Bài tập Toán 10 Phân tích vectơ có đáp án

Bài trước

Tải về

Bài sau

Lớp: Lớp 10

Môn: Toán

Dạng tài liệu: Chuyên đề

Loại: Tài liệu Lẻ

Mức độ: Trung bình

Loại File: Word + PDF

Phân loại: Tài liệu Tính phí

Cách phân tích vectơ theo hai vectơ không cùng phương

A. Ví dụ minh họa phân tích một vectơ
C. Bài tập tự rèn luyện phân tích biểu diễn một vectơ thành hai hay nhiều vectơ

Trong chương trình Toán 10, phần biểu diễn một vectơ thành hai vectơ không cùng phương là nội dung quan trọng trong chuyên đề Vectơ, giúp học sinh hiểu rõ cách phân tích một vectơ theo hai phương cho trước. Bài viết này sẽ hướng dẫn chi tiết cách biểu diễn vectơ theo hai vectơ không cùng phương, kèm theo công thức, ví dụ minh họa và bài tập có đáp án chi tiết, giúp bạn nắm chắc kiến thức và áp dụng hiệu quả trong giải toán hình học.

A. Ví dụ minh họa phân tích một vectơ

Ví dụ 1: Cho hình bình hành $ABCD$. Gọi $M$ là trung điểm của cạnh $BC$. Hãy biểu thị $\overrightarrow{AM}$ $\overrightarrow{AM}$ theo hai vectơ $\overrightarrow{AB}$ $\overrightarrow{AB}$ và $\overrightarrow{AD}$ $\overrightarrow{AD}$.

Hướng dẫn giải

Hình vẽ minh họa:

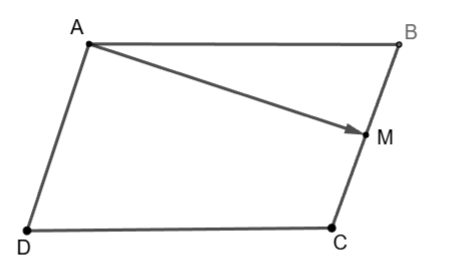
Ta có:

$\overrightarrow{AM} =\frac{1}{2}\left( \overrightarrow{AB} + \overrightarrow{AC} \right)$ $\overrightarrow{AM} =\frac{1}{2}\left( \overrightarrow{AB} + \overrightarrow{AC} \right)$ $=\frac{1}{2}\overrightarrow{AB} + \frac{1}{2} \cdot \frac{1}{2}\left(\overrightarrow{AB} + \overrightarrow{AD} \right)$ $=\frac{1}{2}\overrightarrow{AB} + \frac{1}{2} \cdot \frac{1}{2}\left(\overrightarrow{AB} + \overrightarrow{AD} \right)$ $=\frac{3}{4}\overrightarrow{AB} +\frac{1}{4}\overrightarrow{AD}$ $=\frac{3}{4}\overrightarrow{AB} +\frac{1}{4}\overrightarrow{AD}$

Ví dụ 2: Cho ∆ABC có trọng tâm G. Cho các điểm D, E, F lần lượt là trung điểm của các cạnh BC, CA, AB và I là giao điểm của AD và EF. Đặt $\overrightarrow{u} = \overrightarrow{AE};\ \ \overrightarrow{v} = \overrightarrow{AF}$ $\overrightarrow{u} = \overrightarrow{AE};\ \ \overrightarrow{v} = \overrightarrow{AF}$. Hãy phân tích các vectơ $\overrightarrow{AI},\ \overrightarrow{AG},\ \overrightarrow{DE},\ \overrightarrow{DC}$ $\overrightarrow{AI},\ \overrightarrow{AG},\ \overrightarrow{DE},\ \overrightarrow{DC}$ theo hai vectơ $\overrightarrow{u},\overrightarrow{v}$ $\overrightarrow{u},\overrightarrow{v}$.

Hướng dẫn giải

Hình vẽ minh họa:

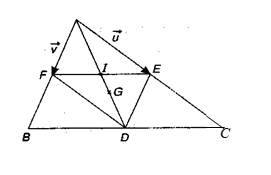
Ta có:

$\overrightarrow{AI} = \frac{1}{2}\overrightarrow{AD} = \frac{1}{2}(\overrightarrow{AE} + \overrightarrow{AF}) = \frac{1}{2}\overrightarrow{u} + \frac{1}{2}\overrightarrow{v})$ $\overrightarrow{AI} = \frac{1}{2}\overrightarrow{AD} = \frac{1}{2}(\overrightarrow{AE} + \overrightarrow{AF}) = \frac{1}{2}\overrightarrow{u} + \frac{1}{2}\overrightarrow{v})$

$\overrightarrow{AG} = \frac{2}{3}\overrightarrow{AD} = \frac{2}{3}\overrightarrow{u} + \frac{2}{3}\overrightarrow{v}$ $\overrightarrow{AG} = \frac{2}{3}\overrightarrow{AD} = \frac{2}{3}\overrightarrow{u} + \frac{2}{3}\overrightarrow{v}$

$\overrightarrow{DE} = \overrightarrow{FA} = - \overrightarrow{AF} = 0.\overrightarrow{u} + ( - 1)\overrightarrow{v}$ $\overrightarrow{DE} = \overrightarrow{FA} = - \overrightarrow{AF} = 0.\overrightarrow{u} + ( - 1)\overrightarrow{v}$

$\overrightarrow{DC} = \overrightarrow{FE} = \overrightarrow{AE} - \overrightarrow{AF} = \overrightarrow{u} - \overrightarrow{v}$ $\overrightarrow{DC} = \overrightarrow{FE} = \overrightarrow{AE} - \overrightarrow{AF} = \overrightarrow{u} - \overrightarrow{v}$

Ví dụ 3: Cho tam giác ABC. Điểm M nằm trên cạnh BC sao cho MB = 2MC. Hãy phân tích vectơ $\overrightarrow{AM}$ $\overrightarrow{AM}$ theo hai vectơ $\overrightarrow{u} = \overrightarrow{AB,}\ \ \ \overrightarrow{v} = \overrightarrow{AC}$ $\overrightarrow{u} = \overrightarrow{AB,}\ \ \ \overrightarrow{v} = \overrightarrow{AC}$.

Hướng dẫn giải

Hình vẽ minh họa:

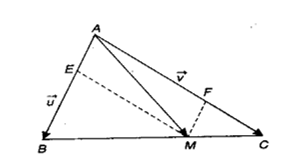
Ta có $\overrightarrow{AM} = \overrightarrow{AB} + \overrightarrow{BM} = \overrightarrow{AB} + \frac{2}{3}\overrightarrow{BC}$ $\overrightarrow{AM} = \overrightarrow{AB} + \overrightarrow{BM} = \overrightarrow{AB} + \frac{2}{3}\overrightarrow{BC}$ mà $\overrightarrow{BC} = \overrightarrow{AC} - \overrightarrow{AB}$ $\overrightarrow{BC} = \overrightarrow{AC} - \overrightarrow{AB}$

⇒ $\overrightarrow{AM} = \overrightarrow{AB} + \frac{2}{3}(\overrightarrow{AC} - \overrightarrow{AB}) = \frac{1}{3}\overrightarrow{u} + \frac{2}{3}\overrightarrow{v}$ $\overrightarrow{AM} = \overrightarrow{AB} + \frac{2}{3}(\overrightarrow{AC} - \overrightarrow{AB}) = \frac{1}{3}\overrightarrow{u} + \frac{2}{3}\overrightarrow{v}$

Ví dụ 4: Cho tam giác $ABC$. Cho các điểm $D,E,H$thỏa mãn đẳng thức:

$\overrightarrow{DB} = \frac{1}{3}\overrightarrow{BC};\ \overrightarrow{AE} = \frac{1}{3}\overrightarrow{AC};\ \ \overrightarrow{AH} = \frac{2}{3}\overrightarrow{AB}$ $\overrightarrow{DB} = \frac{1}{3}\overrightarrow{BC};\ \overrightarrow{AE} = \frac{1}{3}\overrightarrow{AC};\ \ \overrightarrow{AH} = \frac{2}{3}\overrightarrow{AB}$

a) Biểu thị mỗi vectơ $\overrightarrow{AD},\ \overrightarrow{DH},\ \overrightarrow{HE}$ $\overrightarrow{AD},\ \overrightarrow{DH},\ \overrightarrow{HE}$ theo các vectơ $\overrightarrow{AB,}\ \ \ \overrightarrow{AC}$ $\overrightarrow{AB,}\ \ \ \overrightarrow{AC}$

b) Chứng minh $D,E,H$thẳng hàng.

Hướng dẫn giải

Hình vẽ minh họa:

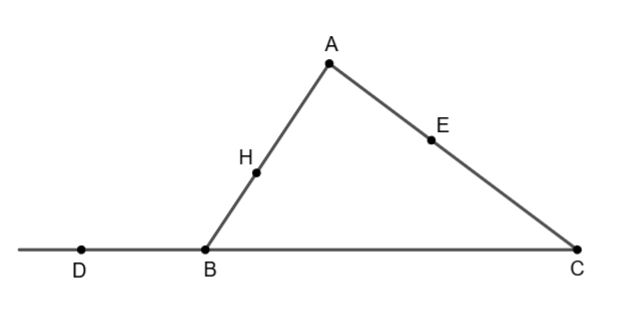
a) Từ

$\overrightarrow{DB} =\frac{1}{3}\overrightarrow{BC}$ $\overrightarrow{DB} =\frac{1}{3}\overrightarrow{BC}$

$\Rightarrow \overrightarrow{AB} -\overrightarrow{AD}= \frac{1}{3}(\overrightarrow{AC} -\overrightarrow{AB})$ $\Rightarrow \overrightarrow{AB} -\overrightarrow{AD}= \frac{1}{3}(\overrightarrow{AC} -\overrightarrow{AB})$

$\Rightarrow \overrightarrow{AD}=\frac{4}{3}\overrightarrow{AB} -\frac{1}{3}\overrightarrow{AC}.$ $\Rightarrow \overrightarrow{AD}=\frac{4}{3}\overrightarrow{AB} -\frac{1}{3}\overrightarrow{AC}.$

Ta có:

$\overrightarrow{AH} = \frac{2}{3}\overrightarrow{AB} \Rightarrow \overrightarrow{DH} - \overrightarrow{DA} = \frac{2}{3}\overrightarrow{AB}$ $\overrightarrow{AH} = \frac{2}{3}\overrightarrow{AB} \Rightarrow \overrightarrow{DH} - \overrightarrow{DA} = \frac{2}{3}\overrightarrow{AB}$

$\Rightarrow \overrightarrow{DH} =\overrightarrow{DA} + \frac{2}{3}\overrightarrow{AB}$ $\Rightarrow \overrightarrow{DH} =\overrightarrow{DA} + \frac{2}{3}\overrightarrow{AB}$ $\Rightarrow\overrightarrow{DH} = - \frac{4}{3}\overrightarrow{AB} +\frac{1}{3}\overrightarrow{AC} +\frac{2}{3}\overrightarrow{AB}$ $\Rightarrow\overrightarrow{DH} = - \frac{4}{3}\overrightarrow{AB} +\frac{1}{3}\overrightarrow{AC} +\frac{2}{3}\overrightarrow{AB}$

$\Rightarrow \overrightarrow{DH} = - \frac{2}{3}\overrightarrow{AB} + \frac{1}{3}\overrightarrow{AC}\ \ \ (1)$ $\Rightarrow \overrightarrow{DH} = - \frac{2}{3}\overrightarrow{AB} + \frac{1}{3}\overrightarrow{AC}\ \ \ (1)$

Lại có:

$\overrightarrow{AE} =\frac{1}{3}\overrightarrow{AC} \Rightarrow \overrightarrow{AH} +\overrightarrow{HE} = \frac{1}{3}\overrightarrow{AC}$ $\overrightarrow{AE} =\frac{1}{3}\overrightarrow{AC} \Rightarrow \overrightarrow{AH} +\overrightarrow{HE} = \frac{1}{3}\overrightarrow{AC}$ $\Rightarrow\overrightarrow{HE} = \frac{1}{3}\overrightarrow{AC} -\overrightarrow{AH}$ $\Rightarrow\overrightarrow{HE} = \frac{1}{3}\overrightarrow{AC} -\overrightarrow{AH}$

$\Rightarrow \overrightarrow{HE} = \frac{1}{3}\overrightarrow{AC} - \frac{2}{3}\overrightarrow{AB}\ \ \ \ (2)$ $\Rightarrow \overrightarrow{HE} = \frac{1}{3}\overrightarrow{AC} - \frac{2}{3}\overrightarrow{AB}\ \ \ \ (2)$

b) Từ (1) và (2) suy ra $\overrightarrow{DH} = \overrightarrow{HE}$ $\overrightarrow{DH} = \overrightarrow{HE}$. Suy ra ba điểm $D,E,H$thẳng hàng và H là trung điểm của DE.

C. Bài tập tự rèn luyện phân tích biểu diễn một vectơ thành hai hay nhiều vectơ

Bài tập 1: Cho tam giác ABC. Điểm M nằm trên cạnh BC sao cho MB= 3MC. Hãy phân tích vectơ $\overrightarrow{AM}$ $\overrightarrow{AM}$ theo hai vectơ $\overrightarrow{u} = \overrightarrow{AB,}\ \ \ \overrightarrow{v} = \overrightarrow{AC}$ $\overrightarrow{u} = \overrightarrow{AB,}\ \ \ \overrightarrow{v} = \overrightarrow{AC}$.

Bài tập 2: Cho hình bình hàng $ABCD$ . Gọi G là trọng tâm tam giác ABC. Biểu thị mỗi vectơ $\overrightarrow{AG},\ \overrightarrow{CG}$ $\overrightarrow{AG},\ \overrightarrow{CG}$ theo các vectơ $\overrightarrow{u} = \overrightarrow{AB,}\ \ \ \overrightarrow{v} = \overrightarrow{AD}$ $\overrightarrow{u} = \overrightarrow{AB,}\ \ \ \overrightarrow{v} = \overrightarrow{AD}$.

Bài tập 3. Cho hình bình hành $ABCD$. Gọi $I$ là trung điểm của $CD$, $G$ là trọng tâm tam giác $BCI$. Đặt $\overrightarrow{a} = \overrightarrow{AB},\overrightarrow{b} = \overrightarrow{AD}$ $\overrightarrow{a} = \overrightarrow{AB},\overrightarrow{b} = \overrightarrow{AD}$. Hãy chứng minh $\overrightarrow{AG} = \frac{5}{6}\overrightarrow{a} + \frac{2}{3}\overrightarrow{b}$ $\overrightarrow{AG} = \frac{5}{6}\overrightarrow{a} + \frac{2}{3}\overrightarrow{b}$.

Bài tập 4. Cho $\Delta ABC$ $\Delta ABC$ có trọng tâm $G$. Gọi $I$ là điểm trên cạnh $BC$sao cho $2CI = 3BI$và $J$là điểm trên $BC$ kéo dài sao cho $5JB = 2JC$. Phân tích $\overrightarrow{AG}$ $\overrightarrow{AG}$theo $\overrightarrow{AI}\ \ ,\ \ \overrightarrow{AJ}$ $\overrightarrow{AI}\ \ ,\ \ \overrightarrow{AJ}$.

Bài tập 5. Cho tam giác $ABC$ , trên cạnh BC lấy M sao cho $BM = 3CM$, trên đoạn AM lấy N sao cho $2AN = 5MN$, G là trọng tâm tam giác $ABC$.

a) Phân tích các vectơ $\overrightarrow{AM},\overrightarrow{BN}$ $\overrightarrow{AM},\overrightarrow{BN}$ qua các vectơ $\overrightarrow{AB}$ $\overrightarrow{AB}$ và $\overrightarrow{AC}$ $\overrightarrow{AC}$.

b) Phân tích các vectơ $\overrightarrow{GC},\ \ \overrightarrow{MN}$ $\overrightarrow{GC},\ \ \overrightarrow{MN}$ qua các vectơ $\overrightarrow{GA}$ $\overrightarrow{GA}$ và $\overrightarrow{GB}$ $\overrightarrow{GB}$.

Tài liệu dài, tải về để xem chi tiết và đầy đủ nhé!

--------------------------------------------------

Qua bài viết này, bạn đã hiểu rõ cách biểu diễn một vectơ thành hai vectơ không cùng phương, nắm vững phương pháp phân tích vectơ và ứng dụng trong hình học. Đây là phần kiến thức nền tảng quan trọng trong chuyên đề Vectơ Toán 10, giúp bạn giải quyết nhanh các dạng bài tập về đẳng thức và hệ phương trình vectơ.

👉 Đừng quên luyện tập thêm nhiều bài tập phân tích vectơ có đáp án chi tiết để củng cố kiến thức, rèn tư duy logic và đạt kết quả cao trong các bài kiểm tra, kỳ thi Toán học.

Tải về

Chọn file muốn tải về: