Cho tam giác ABC có ba cạnh a; b; c. Chứng minh rằng
Chứng minh biểu thức hình học Toán 10 - Có đáp án
Trong chương trình Toán 10, chuyên đề hình học phẳng với các bài toán liên quan đến tam giác ABC và ba cạnh a, b, c là phần kiến thức quan trọng, thường xuất hiện trong các đề kiểm tra và thi học kỳ. Đặc biệt, dạng bài “Cho tam giác ABC có ba cạnh a, b, c. Chứng minh rằng...” yêu cầu học sinh vận dụng nhiều định lý như định lý Cos, định lý Sin, bất đẳng thức tam giác, hoặc kỹ năng biến đổi biểu thức hình học để đưa ra lập luận logic và chính xác.
Bài viết này sẽ hướng dẫn bạn giải từng dạng bài chứng minh liên quan đến tam giác ABC, kèm theo bài tập có đáp án chi tiết, giúp bạn ôn luyện hiệu quả và nâng cao tư duy hình học. Cùng bắt đầu luyện tập ngay để tự tin chinh phục các dạng bài hình học lớp 10!
Bài tập 1. Cho tam giác ABC có BC = a, CA = b, AB = c. Gọi I, p lần lượt là tâm đường tròn nội tiếp, nửa chu vi của tam giác ABC. Chứng minh rằng:
\(\frac{IA^{2}}{c(p - a)} +
\frac{IB^{2}}{a.(p - b)} + \frac{IC^{2}}{b(p - c)} = 2\)
Hướng dẫn giải
Hình vẽ minh họa
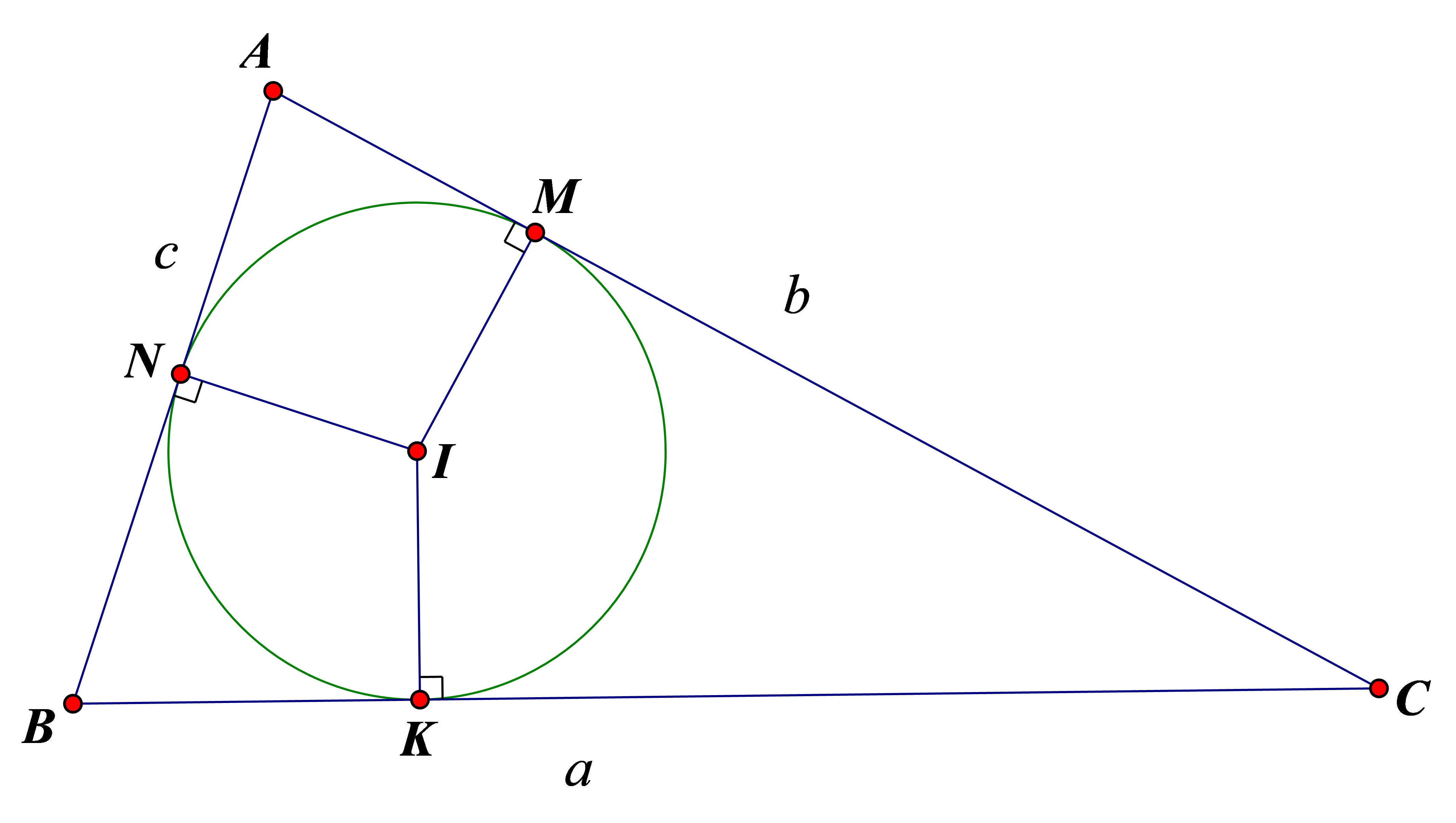
Gọi M, N, K lần lượt là các tiếp điểm của cạnh AC, AB, BC đối với đưởng tròn nội tiếp tam giác ABC.
Ta dễ dàng chứng minh: AM = p - a
\(IA^{2} = r^{2} + AM^{2} =
(\frac{S}{p})^{2} + (p - a)^{2} = \frac{p - a}{p}bc\)
Nên \(\frac{IA_{\ }^{2}\ }{c(p - a)} =
\frac{b}{p}\)
Chứng minh tương tự: \(\frac{IB_{\ }^{2}\
}{a(p - b)} = \frac{c}{p}\); \(\frac{IC_{\ }^{2}\ }{b(p - c)} =
\frac{a}{p}\)
Lúc đó, VT = \(\frac{a + b + c}{p} =
2\)
Bài tập 2. Chứng minh rằng với mọi tam giác ABC ta có:
\(abc(cosA + \cos B + \cos C) = a^{2}(p -
a) + b^{2}(p - b) + c^{2}(p - c)\)
Trong đó p là nữa chu vi của tam giác ABC.
Hướng dẫn giải
Ta có:
\(abc\left( \cos A + \cos B + \cos C
\right)\)
\(= a.\frac{b^{2} + c^{2} - a^{2}}{2} +
b.\frac{a^{2} + c^{2} - b^{2}}{2} + c.\frac{a^{2} + b^{2} -
c^{2}}{2}\)
\(= \frac{1}{2}(ab^{2} + ac^{2} - a^{3} +
ba^{2} + bc^{2} - b^{3} + ca^{2} + cb^{2} - c^{3})\)
\(= \frac{1}{2}(a^{2}b + a^{2}c - a^{3} +
b^{2}a + b^{2}c - b^{3} + c^{2}a + c^{2}b - c^{3})\)
\(= a^{2}.\frac{b + c - a}{2} +
b^{2}.\frac{a + c - b}{2} + c^{2}.\frac{a + b - c}{2}\)
\(= a^{2}(p - a) + b^{2}(p - b) + c^{2}(p -
c)\) (điều phải chứng minh).
Bài tập 3. Xét dạng tam giác ABC thỏa mãn:\(\left\{ \begin{matrix}\dfrac{a^{3} + c^{3} - b^{3}}{a + c - b} = b^{2} \\\sin A.sinC = \dfrac{3}{4} \\\end{matrix} \right.\).
Hướng dẫn giải
Ta có:
\(\frac{a^{3} + c^{3} - b^{3}}{a + c - b} =
b^{2}\) \(\Rightarrow a^{3} + c^{3} -
b^{3} = (a + c)b^{2} - b^{3}\)
\(\Rightarrow a^{3} + c^{3} = (a + c)b^{2}
\Rightarrow a^{2} - ac + c^{2} = b^{2}\)
\(\Rightarrow a^{2} - ac + c^{2} = a^{2} +
c^{2} - 2ac\cos B\)
\(\Rightarrow \cos B = \frac{1}{2}
\Rightarrow B = 60^{0}\)
Do đó\(\sin B = \frac{\sqrt{3}}{2}
\Rightarrow sin^{2}B = \frac{3}{4}\)
\(\sin A.sinC = \frac{3}{4} =
sin^{2}B\) \(\Rightarrow
\frac{a}{2R}.\frac{c}{2R} = \left( \frac{b}{2R} \right)^{2}\)
\(\Rightarrow ac = b^{2} \Rightarrow ac =
a^{2} + c^{2} - 2ac.cosB = a^{2} + c^{2} - ac\)
\(\Rightarrow a^{2} - 2ac + c^{2} = 0
\Rightarrow (a - c)^{2} = 0 \Rightarrow a = c\)
Vậy tam giác cân và có góc 600 nên là tam giác đều.
Bài tập 4. Cho tam giác ABC có ba cạnh là a, b, c. Chứng minh rằng:
\(\frac{a^{2} + b^{2} + c^{2}}{2abc} =
\frac{\cos A}{a} + \frac{\cos B}{b} + \frac{\cos C}{c}\)
Hướng dẫn giải
Ta có
\(\left( \overrightarrow{AB} +\overrightarrow{BC} + \overrightarrow{CA} \right)^{2}\)\(= AB^{2} + BC^{2}+ CA^{2}\)\(+ 2\overrightarrow{AB}.\overrightarrow{BC} +2\overrightarrow{AB}.\overrightarrow{CA}\)\(+2\overrightarrow{BC}\overrightarrow{.CA}\)
\(\Leftrightarrow a^{2} + b^{2} + c^{2} =
2\overrightarrow{AB}.\overrightarrow{BC} +
2\overrightarrow{AB}.\overrightarrow{CA} +
2\overrightarrow{BC}\overrightarrow{.CA}\)
\(\Leftrightarrow a^{2} + b^{2} + c^{2} =
2ac.cosB + 2cb\cos A + 2ab.cosC\)
\(\Leftrightarrow \frac{a^{2} + b^{2} +
c^{2}}{2abc} = \frac{\cos A}{a} + \frac{\cos B}{b} + \frac{\cos
C}{c}\)
----------------------------------------------------
Thông qua bài viết, bạn đã được củng cố cách tiếp cận và lập luận chặt chẽ khi giải các bài toán chứng minh liên quan đến tam giác ABC với ba cạnh a, b, c trong chương trình Toán 10. Việc hiểu rõ mối quan hệ giữa các cạnh và góc trong tam giác, kết hợp với kỹ năng biến đổi biểu thức chính xác sẽ giúp bạn dễ dàng xử lý các bài tập ở mọi mức độ từ cơ bản đến nâng cao.
