Chứng minh đẳng thức vectơ có chứa tích của vectơ với một số
Bài tập chứng minh đẳng thức vectơ có đáp án chi tiết
Trong chương trình Toán 10, dạng bài chứng minh đẳng thức vectơ có chứa tích của vectơ với một số là phần kiến thức quan trọng giúp học sinh nắm vững các quy tắc cộng, trừ và nhân vectơ với số thực. Đây là nền tảng để giải quyết các bài toán hình học phức tạp và chứng minh các quan hệ hình học bằng phương pháp vectơ. Bài viết dưới đây sẽ hướng dẫn chi tiết cách chứng minh đẳng thức vectơ chứa tích vectơ, kèm ví dụ minh họa và bài tập có đáp án, giúp bạn hiểu bản chất và rèn luyện kỹ năng giải Toán hiệu quả.
A. Phương pháp chứng minh đẳng thức
Dùng quy tắc 3 điểm, quy tắc đường chéo hình bình hành, cặp vectơ bằng nhau trong hình bình hành.
Dùng tính chất trung điểm, trọng tâm – ba điểm thẳng hàng:
- A, B, C thẳng hàng ⇔ ∃k ≠ 0:
\(\overrightarrow{AB} =
k\overrightarrow{AC}\). - M là trung điểm AB ⇔ \(\overrightarrow{MA}
+ \overrightarrow{MB} = \overrightarrow{0}\) ⇔ \(\overrightarrow{OA} + \overrightarrow{OB} =
2\overrightarrow{OM}\) (điểm O tuỳ ý).
- G là trọng tâm ∆ABC ⇔ \(\overrightarrow{GA}
+ \overrightarrow{GB} + \overrightarrow{GC} =
\overrightarrow{0}\) ⇔ \(\overrightarrow{OA} + \overrightarrow{OB} +
\overrightarrow{OC} = 3\overrightarrow{OG}\) (điểm O tuỳ ý).
B. Ví dụ minh họa chứng minh đẳng thức vectơ
Ví dụ 1: Gọi M, N lần lượt là trung điểm của hai đoạn thẳng AB và \(CD\). Chứng minh: \(2\overrightarrow{MN} = \overrightarrow{AC} +
\overrightarrow{BD}\).
Hướng dẫn giải
Hình vẽ minh họa:
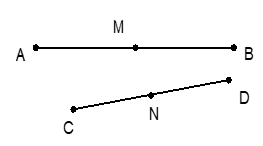
Ta có:
\(VP = \overrightarrow{AC} +
\overrightarrow{BD}\)
\(= \overrightarrow{AM} +
\overrightarrow{MN} + \overrightarrow{NC} + \overrightarrow{BM} +
\overrightarrow{MN} + \overrightarrow{ND}\)
\(= 2\overrightarrow{MN} +
\overrightarrow{AM} + \overrightarrow{BM} + \overrightarrow{ND} +
\overrightarrow{NC} = 2\overrightarrow{MN}\)
Ví dụ 2: Cho tứ giác \(ABCD\) . Gọi \(M,\ N\) tương ứng là trung điểm của các cạnh \(AB,\ CD\). Gọi \(I\)là trung điểm của \(MN\).Chứng minh rằng
a) \(\overrightarrow{BC} +
\overrightarrow{AD} = 2\overrightarrow{MN} = \overrightarrow{AC} +
\overrightarrow{BD}\). b) \(\overrightarrow{OA} +
\overrightarrow{OB} + \overrightarrow{OC} + \overrightarrow{OD} =
4\overrightarrow{OI},\ \forall O\)
Hướng dẫn giải
Hình vẽ minh họa:
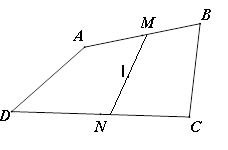
a) Ta có:
\(\overrightarrow{BC} +
\overrightarrow{AD} = \overrightarrow{BM} + \overrightarrow{MN} +
\overrightarrow{NC} + \overrightarrow{AM} + \overrightarrow{MN} +
\overrightarrow{ND}\)
\(= 2\overrightarrow{MN} + \left(
\overrightarrow{BM} + \overrightarrow{AM} \right) + \left(
\overrightarrow{NC} + \overrightarrow{ND} \right)\)
\(= 2\overrightarrow{MN} +
\overrightarrow{0} + \overrightarrow{0} =
2\overrightarrow{MN}\)
\(\overrightarrow{BC} +
\overrightarrow{AD} = \overrightarrow{BA} + \overrightarrow{AC} +
\overrightarrow{AB} + \overrightarrow{BD}\)
\(= \left( \overrightarrow{BA} +
\overrightarrow{AB} \right) + \overrightarrow{AC} +
\overrightarrow{BD}\)
\(= \overrightarrow{0} +
\overrightarrow{AC} + \overrightarrow{BD} = \overrightarrow{AC} +
\overrightarrow{BD}\)
Vậy \(\overrightarrow{BC} +
\overrightarrow{AD} = 2\overrightarrow{MN} = \overrightarrow{AC} +
\overrightarrow{BD}\)
b) Vì \(M,\ N\) tương ứng là trung điểm của các cạnh \(AB,\ CD\) nên ta có
\(\overrightarrow{IA} +
\overrightarrow{IB} = 2\overrightarrow{IM};\ \ \overrightarrow{IC} +
\overrightarrow{ID} = 2\overrightarrow{IN}\)
\(I\) là trung điểm của \(MN\) nên \(\overrightarrow{IM} + \overrightarrow{IN} =
\overrightarrow{0}\)
Do đó \(\overrightarrow{IA} +
\overrightarrow{IB} + \overrightarrow{IC} + \overrightarrow{ID} =
2(\overrightarrow{IM} + \overrightarrow{IN}) = 2.\overrightarrow{0} =
\overrightarrow{0}\)
Với mọi điểm \(O\) ta có \(\overrightarrow{IA} + \overrightarrow{IB} +
\overrightarrow{IC} + \overrightarrow{ID} =
\overrightarrow{0}\)
\(\Rightarrow \overrightarrow{OA} -
\overrightarrow{OI} + \overrightarrow{OB} - \overrightarrow{OI} +
\overrightarrow{OC} - \overrightarrow{OI} + \overrightarrow{ID} -
\overrightarrow{OI} = \overrightarrow{0}\)
\(\Rightarrow \overrightarrow{OA} +
\overrightarrow{OB} + \overrightarrow{OC} + \overrightarrow{ID} =
4\overrightarrow{OI}.\)
Ví dụ 3: Cho hình bình hành ABCD. Chứng minh rằng: \(\overrightarrow{AB} + 2\overrightarrow{AC} +
\overrightarrow{AD} = 3\overrightarrow{AC}\).
Hướng dẫn giải
Áp dụng quy tắc hình bình hành ta có \(\overrightarrow{AB} + \overrightarrow{AD} =
\overrightarrow{AC}\)
⇒ \(VT = \overrightarrow{AC} +
2\overrightarrow{AC} = 3\overrightarrow{AC} =
\overrightarrow{VP}\) (điều phải chứng minh).
Ví dụ 4: Cho tam giác \(ABC\). Gọi \(M\), \(N\), \(P\) lần lượt là trung điểm của \(BC\), \(CA\), \(AB\). Chứng minh rằng:
a) \(\overrightarrow{AM} +
\overrightarrow{BN} + \overrightarrow{CP} =
\overrightarrow{0}\). b) \(\overrightarrow{AP} +
\frac{1}{2}\overrightarrow{BC} = \overrightarrow{AN}\) c) \(\overrightarrow{BC} +
2\overrightarrow{MP} = \overrightarrow{BA}\)
Hướng dẫn giải
Hình vẽ minh họa:
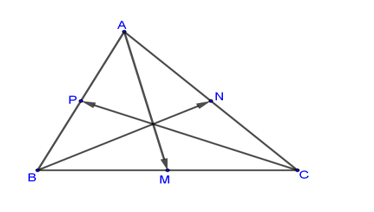
a) Ta có
\(\overrightarrow{AM} + \overrightarrow{BN}+ \overrightarrow{CP}\)
\(= \frac{1}{2}\left( \overrightarrow{AB} +\overrightarrow{AC} \right) + \frac{1}{2}\left( \overrightarrow{BA} +\overrightarrow{BC} \right) + \frac{1}{2}\left( \overrightarrow{CA} +\overrightarrow{CB} \right)\)
\(= \frac{1}{2}\left( \overrightarrow{AB} +\overrightarrow{BA} \right) + \frac{1}{2}\left( \overrightarrow{AC} +\overrightarrow{CA} \right)\)\(+ \frac{1}{2}\left( \overrightarrow{BC} +\overrightarrow{CB} \right) = \overrightarrow{0}\).
b) Ta có:
\(\overrightarrow{AP} =
\frac{1}{2}\overrightarrow{AB};\ \overrightarrow{AN} =
\frac{1}{2}\overrightarrow{AC}\).
Do đó:
\(\overrightarrow{AP} +
\frac{1}{2}\overrightarrow{BC} = \frac{1}{2}\overrightarrow{AB} +
\frac{1}{2}\overrightarrow{BC}\)\(= \frac{1}{2}(\overrightarrow{AB} +
\overrightarrow{BC}) = \frac{1}{2}\overrightarrow{AC} =
\overrightarrow{AN}.\)
Vậy \(\overrightarrow{AP} +
\frac{1}{2}\overrightarrow{BC} = \overrightarrow{AN}\)
c) Ta có: \(\overrightarrow{MP} =
\frac{1}{2}\overrightarrow{CA} \Rightarrow 2\overrightarrow{MP} =
\overrightarrow{CA}.\)
Do đó \(\overrightarrow{BC} +
2\overrightarrow{MP} = \overrightarrow{BC} + \overrightarrow{CA} =
\overrightarrow{BA}.\)
Vậy \(\overrightarrow{BC} +
2\overrightarrow{MP} = \overrightarrow{BA}\).
C. Bài tập tự rèn luyện chứng minh đẳng thức vectơ có đáp án chi tiết
Bài tập 1: Cho ∆ABC. Gọi M, N lần lượt là trung điểm của AB, AC. Chứng minh rằng: \(3\overrightarrow{MN} -
\overrightarrow{BN} + \overrightarrow{CM} =
\overrightarrow{0}\).
Bài tập 2: Cho \(\Delta ABC\) có trọng tâm \(G\). Chứng minh \(\overrightarrow{AG\ } = \frac{1}{3}\left(
\overrightarrow{AB\ } + \overrightarrow{AC\ } \right)\).
Bài tập 3. Chứng minh rằng nếu G và G’ lần lượt là trọng tâm tam giác ABC và A’B’C’ thì \(3\overrightarrow{GG'}
= \overrightarrow{AA'} + \overrightarrow{BB'} +
\overrightarrow{CC'}\).
Bạn muốn xem toàn bộ tài liệu? Hãy nhấn Tải về ngay!
---------------------------------------------------------------
Qua bài viết này, bạn đã được hướng dẫn cụ thể cách chứng minh đẳng thức vectơ có chứa tích của vectơ với một số, cùng các ví dụ minh họa và bài tập chi tiết trong chuyên đề Vectơ Toán 10. Kiến thức này không chỉ giúp bạn củng cố tư duy đại số và hình học, mà còn là bước chuẩn bị quan trọng cho các chương học tiếp theo như tọa độ trong mặt phẳng và phương trình đường thẳng.
👉 Hãy thường xuyên luyện tập bài tập chứng minh đẳng thức vectơ có đáp án chi tiết để nâng cao kỹ năng, tăng tốc độ làm bài và đạt điểm tối đa trong các kỳ thi môn Toán.
