Chứng minh hai vectơ bằng nhau
Cách chứng minh hai vectơ cùng phương và bằng nhau
Trong chương trình Toán 10, kiến thức về vectơ đóng vai trò quan trọng trong việc hiểu sâu hơn về hình học và đại số. Một trong những nội dung nền tảng là chứng minh hai vectơ bằng nhau, giúp học sinh nắm vững bản chất của phương, hướng và độ dài vectơ.
Bài viết dưới đây sẽ hướng dẫn chi tiết cách chứng minh hai vectơ bằng nhau, kèm ví dụ minh họa và bài tập có lời giải chi tiết, giúp bạn củng cố lý thuyết, nâng cao kỹ năng làm bài và đạt kết quả tốt trong các kỳ kiểm tra.
A. Cách chứng minh 2 vectơ bằng nhau
Phương pháp: Ta chứng minh hai vectơ đó cùng hướng và cùng độ dài. Thường sử dụng các đẳng thức vectơ bằng nhau trong hình bình hành.
B. Ví dụ minh họa chứng minh 2 vectơ bằng nhau
Ví dụ 1: Cho tứ giác 
\(ABCD\). Chứng minh rằng tứ giác đó là hình bình hành khi và chỉ khi \(\overrightarrow{AB} =
\overrightarrow{DC}\)?
Hướng dẫn giải
Hình vẽ minh họa:
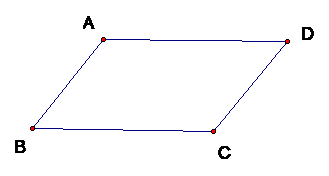
+ Nếu tứ giác ABCD là hình bình hành thì \(AB = DC\) và hai vectơ \(\overrightarrow{AB};\overrightarrow{DC}\) cùng hướng. Vậy \(\overrightarrow{AB} =
\overrightarrow{DC}\)
+ Ngược lại, nếu \(\overrightarrow{AB} =
\overrightarrow{DC}\) thì \(AB =
DC\) và \(AB//DC\).
Vậy tứ giác \(ABCD\) là hình bình hành.
Ví dụ 2: Cho tứ giác \(ABCD\). Gọi M, N, P và Q lần lượt là trung điểm của các cạnh AB, BC, CD và DA. Chứng minh: \(\overrightarrow{NP} =
\overrightarrow{MQ}\) và \(\overrightarrow{PQ} =
\overrightarrow{NM}\)?
Hướng dẫn giải
Hình vẽ minh họa:
Vì MN là đường trung bình của tam giác BAC nên ta có: \(\left\{ \begin{matrix}MN//AC \\MN = \dfrac{1}{2}AC\end{matrix} \right.\)
Mặt khác, PQ là đường trung bình của tam giác DAC nên ta có: \(\left\{ \begin{matrix}PQ//AC \\PQ = \dfrac{1}{2}AC\end{matrix} \right.\)
Từ đó suy ra \(\left\{ \begin{matrix}
MN//PQ \\
MN = PQ
\end{matrix} \right.\)
Hay tứ giác MNPQ là hình bình hành. Do đó ta có: \(\overrightarrow{NP} = \overrightarrow{MQ}\) và \(\overrightarrow{PQ} =
\overrightarrow{NM}\)
Ví dụ 3: Cho hình bình hành \(ABCD\). Gọi \(M,\
N\) lần lượt là trung điểm của \(BC\) và \(AD,I\)là giao điểm của \(AM\) và \(BN\), \(K\)là giao điểm của \(DM\) và \(CN\). Chứng minh \(\overrightarrow{AM} =
\overrightarrow{NC}\); \(\overrightarrow{DK} =
\overrightarrow{NI}.\)
Hướng dẫn giải
Hình vẽ minh họa:
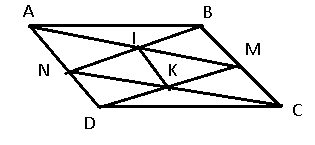
a) Vì \(ABCD\) là hình bình hành nên suy ra \(AN//MC\) và \(AN = MC = \frac{1}{2}BC.\).
Do đó \(ANCM\) là hình bình hành. Vậy \(\overrightarrow{AM} =
\overrightarrow{NC}\).
b) Xét tam giác \(ADM\) ta có \(IK\) là đường trung bình nên \(IK//AD \Rightarrow KI//ND\) và \(IK = \frac{1}{2}AD;\ ND = \frac{1}{2}AD
\Rightarrow IK = DN.\)
Từ đó suy ra \(NDKI\) là hình bình hành. Vậy \(\overrightarrow{DK} =
\overrightarrow{NI}.\)
Ví dụ 4: Cho hình bình hành \(ABCD\). Gọi \(E,\
F\) lần lượt là trung điểm của \(AB\) và \(CD\). Đường chéo \(BD\) cắt \(AF\) tai \(G\), cắt \(CE\) tại \(H\). Chứng minh:
a) \(\overrightarrow{DG} =
\overrightarrow{GH} = \overrightarrow{HB}\) b) \(\overrightarrow{AH} =
\overrightarrow{GC}.\)
Hướng dẫn giải
Hình vẽ minh họa:
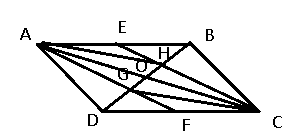
a) Gọi \(O\) là tâm của hình bình hành, ta có \(G\),\(H\) lần lượt là trọng tâm các tam giác \(ADC\) và \(ABC.\)
Suy ra: \(DG = 2GO = \frac{2}{3}OD;BH = 2HO
= \frac{2}{3}OB\)
Ta lại có \(OD = OB\)
Từ đó suy ra \(DG = BH = 2GO = 2HO
\Rightarrow DG = BH = GH.\)
Các vectơ \(\overrightarrow{DG},\
\overrightarrow{GH},\ \overrightarrow{HB}\) cùng hướng và cùng độ dài nên \(\overrightarrow{DG} =
\overrightarrow{GH} = \overrightarrow{HB}\).
b) Ta có tứ giác \(AECF\) là hình bình hành nên \(AF//CE\) và \(AF = CE\).
Suy ra \(AG//CH\)
Ta lại có \(AG = \frac{2}{3}AF;\ CH =\frac{2}{3}CE\). Mà \(AF = CE\) nên \(AG = \ CH\).
Từ đó suy ra \(AGCH\) là hình bình hành. Vậy \(\overrightarrow{AH} =
\overrightarrow{GC}.\)
C. Bài tập tự rèn luyện chứng minh hai vectơ bằng nhau có lời giảis
Bài tập 1: Cho tam giác \(ABC\) có trực tâm \(H\). Gọi \(D\) là điểm đối xứng với \(B\) qua tâm \(O\) của đường tròn ngoại tiếp tam giác \(ABC\). Chứng minh \(\overrightarrow{HA} = \overrightarrow{CD}\) và \(\overrightarrow{AD} =
\overrightarrow{HC}\).
Bài tập 2. Cho tam giác \(ABC\). Vẽ \(D\) đối xứng với \(A\)qua \(B\), \(E\) đối xứng với \(B\) qua \(C\) và \(F\) đối xứng với \(C\) qua \(A\). Gọi \(G\)là giao điểm của trung tuyến \(AM\)của tam giác \(ABC\) với trung tuyến \(DN\) của tam giác \(DEF\). Gọi \(I,\
K\)lần lượt là trung điểm của \(GA\) và \(GD\). Chứng minh rằng
a) \(\overrightarrow{AB} =
\overrightarrow{NM}\) b) \(\overrightarrow{MK} =
\overrightarrow{NI}\)
Bài tập 3: Cho tam giác \(ABC\)và \(M\)là một điểm không thuộc các cạnh của tam giác. Gọi \(D\), \(E\) , \(F\) lần lượt là trung điểm của \(AB,\ BC,\ CA\). Vẽ \(P\) đối xứng với \(M\) qua \(D\), điểm \(Q\) đối xứng với \(P\) qua \(E\), điểm \(N\) đối xứng với \(Q\) qua \(F\). Chứng minh rằng \(\overrightarrow{MA} =
\overrightarrow{AN}\).
Bạn muốn xem toàn bộ tài liệu? Hãy nhấn Tải về ngay!
------------------------------------------------
Qua bài viết này, bạn đã được hệ thống đầy đủ lý thuyết về hai vectơ bằng nhau, cùng phương pháp chứng minh và các bài tập có đáp án minh họa cụ thể.
👉 Việc hiểu rõ cách chứng minh hai vectơ bằng nhau không chỉ giúp bạn nắm chắc phần Vectơ Toán 10, mà còn là nền tảng cho các chuyên đề sau như Tổng – Hiệu vectơ, Độ dài vectơ, và Ứng dụng trong tọa độ Oxy.
