Khái niệm vectơ Toán 10
Vectơ là gì? Tính chất của vectơ
Trong chương trình Toán 10, phần vectơ là nội dung nền tảng quan trọng của hình học, giúp học sinh hiểu sâu hơn về vị trí, hướng và độ dài của đoạn thẳng có hướng. Việc nắm vững khái niệm vectơ là bước khởi đầu để học tốt các chuyên đề tiếp theo như tích vô hướng, tọa độ vectơ, phương trình đường thẳng trong mặt phẳng. Bài viết này sẽ giúp bạn hiểu rõ bản chất vectơ, các tính chất cơ bản và cách biểu diễn vectơ trên mặt phẳng, kèm ví dụ minh họa dễ hiểu, phục vụ hiệu quả cho việc ôn tập lý thuyết Toán 10.
1. Định nghĩa vectơ
Vectơ là đoạn thẳng có hướng, nghĩa là trong hai điểm mút của đoạn thẳng đã chỉ rõ điểm nào là điểm đầu, điểm nào là điểm cuối.
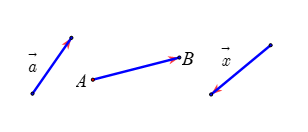
- Vectơ có điểm đầu là A, điểm cuối là B ta kí hiệu :
\(\overrightarrow{AB}\) - Vectơ còn được kí hiệu là: \(\overrightarrow{a},\overrightarrow{b},\overrightarrow{x},\overrightarrow{y},...\)
- Vectơ – không là vectơ có điểm đầu trùng điểm cuối. Kí hiệu là \(\overrightarrow{0}\).
2. Hai vectơ cùng phương, cùng hướng.
- Đường thẳng đi qua điểm đầu và điểm cuối của vectơ gọi là giá của vectơ.
- Hai vectơ có giá song song hoặc trùng nhau gọi là hai vectơ cùng phương.
- Hai vectơ cùng phương thì hoặc cùng hướng hoặc ngược hướng.
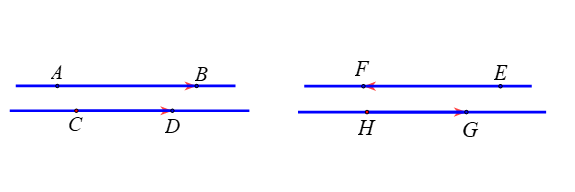
Ví dụ: Ở hình vẽ trên trên (hình 2) thì hai vectơ \(\overrightarrow{AB}\) và \(\overrightarrow{CD}\) cùng hướng còn \(\overrightarrow{EF}\) và \(\overrightarrow{HG}\) ngược hướng.
Đặc biệt: vectơ – không cùng hướng với mọi véc tơ.
3. Hai vectơ bằng nhau
- Độ dài đoạn thẳng \(AB\) gọi là độ dài vectơ \(\overrightarrow{AB}\), kí hiệu \(\left| \overrightarrow{AB}
\right|\). Vậy \(\left| \overrightarrow{AB} \right| =
AB\).
Hai vectơ bằng nhau nếu chúng cùng hướng và cùng độ dài.
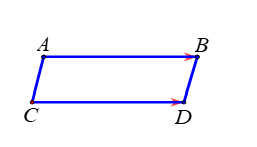
Ví dụ: Cho hình bình hành \(ABCD\) khi đó \(\overrightarrow{AB} =
\overrightarrow{CD}\).
-----------------------------------------------------------------
Nắm vững khái niệm vectơ là chìa khóa giúp bạn học tốt phần hình học giải tích Toán 10 và dễ dàng tiếp cận các chuyên đề nâng cao ở lớp 11, 12. Hy vọng qua bài viết này, bạn đã hiểu rõ vectơ là gì, các ký hiệu và tính chất cơ bản để vận dụng linh hoạt trong bài tập.
👉 Đừng quên tham khảo thêm các bài học lý thuyết Toán 10 khác như Tổng và hiệu của hai vectơ hay Vectơ cùng phương, cùng hướng để củng cố kiến thức toàn diện hơn!
