Tìm tập hợp điểm thỏa mãn đẳng thức vectơ
Cách tìm tập hợp điểm thỏa mãn đẳng thức vectơ
Trong chương trình Toán 10, dạng bài tìm tập hợp điểm thỏa mãn đẳng thức vectơ là nội dung trọng tâm của chuyên đề Vectơ, giúp học sinh rèn luyện kỹ năng biến đổi, chứng minh và nhận dạng hình học qua vectơ. Bài viết này sẽ hướng dẫn chi tiết cách xác định tập hợp điểm dựa vào đẳng thức vectơ, kèm theo bài tập minh họa và đáp án chi tiết, giúp bạn hiểu sâu và vận dụng chính xác trong các đề thi và bài kiểm tra.
A. Cách xác định tập hợp điểm bằng vectơ
Để xác định 1 điểm thỏa mãn đẳng thức vectơ, ta làm như sau
- Biến đổi đẳng thức về dạng
\(\overrightarrow{AM} = \overrightarrow{u}\), trong đó A và \(\overrightarrow{u}\) là cố định. - Lấy A làm gốc để dựng vectơ bằng \(\overrightarrow{u}\) điểm ngọn chính là điểm M cần tìm.
B. Ví dụ minh họa tìm tập hợp điểm thỏa mãn đẳng thức vectơ
Ví dụ 1: Cho hình chữ nhật \(ABCD\) có \(AB =
a,\ AD = a\sqrt{3}\).
a) Độ dài của vectơ \(\overrightarrow{DC} -
\overrightarrow{DB} + \overrightarrow{AB}\).
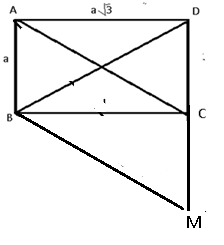
b) Xác định điểm \(M\) sao cho \(\overrightarrow{DC} + \overrightarrow{BD} +
\overrightarrow{AB} = \overrightarrow{BM}.\)
Hướng dẫn giải
a) Hình vẽ minh họa:
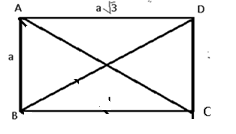
Ta có:
\(\overrightarrow{DC} - \overrightarrow{DB} + \overrightarrow{AB} =\overrightarrow{BC} + \overrightarrow{AB} = \overrightarrow{AC}\)
\(\Rightarrow \left| \overrightarrow{DC} - \overrightarrow{DB} +\overrightarrow{AB} \right|\)\(= \left| \overrightarrow{AC} \right| = AC =\sqrt{a^{2} + (a\sqrt{3})^{2}} = 2a.\)
Vậy \(\left| \overrightarrow{DC} -
\overrightarrow{DB} + \overrightarrow{AB} \right| = 2a.\)
b) Ta có: \(\overrightarrow{DC} +
\overrightarrow{BD} + \overrightarrow{AB} =
\overrightarrow{AC}.\)
Mà \(\overrightarrow{DC} +
\overrightarrow{BD} + \overrightarrow{AB} = \overrightarrow{BM}
\Rightarrow \overrightarrow{AC} = \overrightarrow{BM}.\)
Vậy \(M\) là điểm thứ tư của hình bình hành \(ABMC\) hay \(M\)đối xứng với \(D\) qua \(C\).
Ví dụ 2: Cho tam giác \(ABC\), gọi \(D,E,F\) theo thứ tự là trung điểm của \(BC,CA,AB.\).
a) Xác định vectơ \(A\overrightarrow{F} -
\overrightarrow{BD} + \overrightarrow{CE}\).
b) Xác định điểm \(M\) sao cho \(A\overrightarrow{F} - \overrightarrow{BD} +
\overrightarrow{CE} = \overrightarrow{MA}.\)
c) Chứng minh \(\overrightarrow{MC} =
\overrightarrow{AB}\).
Hướng dẫn giải
a) Hình vẽ minh họa:
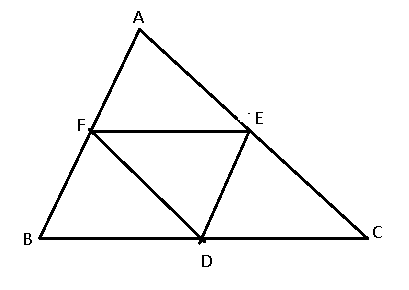
Ta có: \(A\overrightarrow{F} -
\overrightarrow{BD} + \overrightarrow{CE} = A\overrightarrow{F} +
\overrightarrow{DB} + \overrightarrow{CE}\)
Mà \(\overrightarrow{DB} =
\overrightarrow{EF};\ \overrightarrow{CE} =
\overrightarrow{EA}\), do đó:
\(A\overrightarrow{F} - \overrightarrow{BD} +\overrightarrow{CE}\)\(= A\overrightarrow{F} + \overrightarrow{EF} +\overrightarrow{EA}\)\(= \overrightarrow{EA} + A\overrightarrow{F} +\overrightarrow{EF} = \overrightarrow{CB}.\)
b) Ta có: \(A\overrightarrow{F} -
\overrightarrow{BD} + \overrightarrow{CE} =
\overrightarrow{CB}.\)
Mà giả thiết \(A\overrightarrow{F} -\overrightarrow{BD} + \overrightarrow{CE} = \overrightarrow{MA}\)
\(\Rightarrow \overrightarrow{CB} = \overrightarrow{MA}\)\(\Rightarrow\overrightarrow{AM} = \overrightarrow{BC}\)
Vậy \(M\) là điểm thứ tư của hình bình hành \(ABCM\) hay \(M\) đối xứng với \(B\) qua \(E.\)
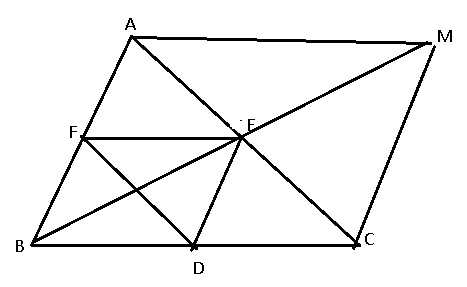
c) Vì \(ABCM\) là hình bình hành nên \(\overrightarrow{MC} =
\overrightarrow{AB}\).
-------------------------------------------------------
Qua bài viết này, bạn đã được hướng dẫn cụ thể cách tìm tập hợp điểm thỏa mãn đẳng thức vectơ thông qua các phương pháp biến đổi và suy luận hình học. Đây là kỹ năng quan trọng không chỉ trong chuyên đề vectơ Toán 10, mà còn hỗ trợ hiệu quả cho các chương sau như phương trình đường thẳng hay tọa độ trong mặt phẳng.
