Tìm tọa độ điểm D để biểu thức vectơ đạt giá trị nhỏ nhất
Tìm giá trị nhỏ nhất của biểu thức vectơ
Trong chương trình Toán 10, chuyên đề hình học giải tích không chỉ giúp học sinh rèn luyện kỹ năng tính toán tọa độ mà còn phát triển tư duy hình học không gian thông qua các bài toán liên quan đến vectơ. Một trong những dạng bài thường gặp là tìm tọa độ điểm D để biểu thức vectơ đạt giá trị nhỏ nhất, yêu cầu học sinh kết hợp giữa kiến thức về vectơ, độ dài đoạn thẳng, và bài toán cực trị hình học.
Bài viết này sẽ hướng dẫn chi tiết phương pháp giải loại bài tập này theo từng bước, từ việc phân tích hình học đến áp dụng công thức tọa độ. Ngoài ra, bạn sẽ được luyện tập qua các bài tập minh họa có đáp án chi tiết, giúp nắm chắc kiến thức và nâng cao kỹ năng giải nhanh trong các đề kiểm tra, thi học kỳ hoặc ôn thi học sinh giỏi. Hãy cùng bắt đầu!
Bài tập 1. Cho tam giác 
\(ABC\) đều cạnh \(a\) nội tiếp đường tròn \((O)\), \(M\) là một điểm thay đổi trên \((O)\). Gọi \(x,y\) lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức \(\left|
\overrightarrow{MA} + \overrightarrow{MB} - \overrightarrow{MC}
\right|\). Tính tổng \(x;y\).
Hướng dẫn giải
Hình vẽ minh họa
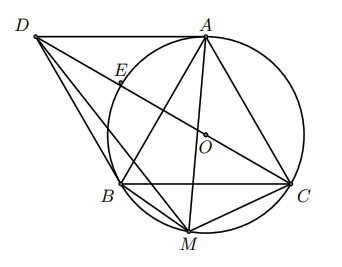
Dựng hình bình hành DBCA. Ta có:
\(\left| \overrightarrow{MA} +
\overrightarrow{MB} - \overrightarrow{MC} \right|\)
\(= \left| \overrightarrow{MD} +
\overrightarrow{DA} + \overrightarrow{MD} + \overrightarrow{DB} -
\overrightarrow{MD} - \overrightarrow{DC} \right|\)
\(= \left| \overrightarrow{MD} \right| =
MD\)
Gọi E là giao điểm khác C của DC với (O).
Áp dụng bất đẳng thức tam giác ta có: \(\left\{ \begin{matrix}
MD \geq DO - OM = DO - OE = DE \\
MD \leq DO + OM = DO + OE = DC \\
\end{matrix} \right.\)
Dấu bằng xảy ra khi và chỉ khi M trùng E và M trùng C.
Vậy \(x + y = DE + DC\) \(= DC - CE + DC\)
\(= 2DC - 2OC = 2.\frac{a\sqrt{3}}{2} -
2.\frac{a}{\sqrt{3}} = \frac{4a}{\sqrt{3}}\)
Bài tập 2. Trong mặt phẳng tọa độ \(Oxy\), cho tọa độ \(A(1; - 4),B(4;5),C(0; - 7)\). Một điểm \(M \in Ox\) bất kì. Tìm giá trị nhỏ nhất của biểu thức:\(T = 2\left|
\overrightarrow{MA} + 2\overrightarrow{MB} \right| + 3\left|
\overrightarrow{MB} + \overrightarrow{MC} \right|\)?
Hướng dẫn giải
Ta có: \(M \in Ox \Rightarrow
M(x;0)\)
Lại có: \(\left\{ \begin{matrix}
\overrightarrow{MA} = (1 - x; - 4) \\
\overrightarrow{MB} = (4 - x;5) \\
\overrightarrow{MC} = ( - x; - 7) \\
\end{matrix} \right.\)
Suy ra \(\left\{ \begin{matrix}
\overrightarrow{MA} + 2\overrightarrow{MB} = (9 - 3x;6) \\
\overrightarrow{MB} + \overrightarrow{MC} = (4 - 2x; - 2) \\
\end{matrix} \right.\)
Ta có:
\(T = 2\left| \overrightarrow{MA} +
2\overrightarrow{MB} \right| + 3\left| \overrightarrow{MB} +
\overrightarrow{MC} \right|\)
\(= 2\sqrt{(9 - 3x)^{2} + 6^{2}} +
3\sqrt{(4 - 2x)^{2} + ( - 2)^{2}}\)
\(= 6\left( \sqrt{(3 - x)^{2} + 2^{2}} +
\sqrt{(2 - x)^{2} + ( - 1)^{2}} \right) = 6(ME + MF)\) (Với \(E(3;2),F(2; - 1)\))
Lại có: \(\overrightarrow{EF} = ( - 1; - 3)
\Rightarrow \left| \overrightarrow{EF} \right| = \sqrt{10}\)
Mà \(ME + MF \geq EF \Rightarrow T \geq
6\sqrt{10}\)
Dấu đẳng thức xảy ra khi M là giao điểm của EF và Ox => \(M\left( \frac{7}{3};0 \right)\)
Vậy biểu thức T đạt giá trị nhỏ nhất là \(6\sqrt{10}\).
Bài tập 3. Cho hình vuông \(ABCD\) cạnh \(a\). Gọi \(M\) là trung điểm của \(AB\), lấy các điểm \(P,Q,R\) lần lượt là các điểm thay đổi trên các cạnh \(BC,AC,AD\) sao cho \(\widehat{PMR} = 90^{0}\). Tìm giá trị nhỏ nhất của biểu thức \(\left|
\overrightarrow{MP} + \overrightarrow{MQ} + \overrightarrow{MR}
\right|\).
Hướng dẫn giải
Hình vẽ minh họa
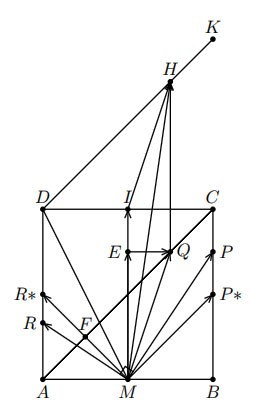
Đặt \(\left| \overrightarrow{AR} \right| =
x;\left| \overrightarrow{BP} \right| = y;\left| \overrightarrow{ME}
\right| = z;\left| \overrightarrow{EQ} \right| = t\)
Ta có: \(\Delta AMR\sim\Delta BPM\) \(\Rightarrow \left\{ \begin{matrix}
xy = \frac{a^{2}}{4} \\
x + y \geq 2\sqrt{xy} = a \\
\end{matrix} \right.\)
Dấu bằng xảy ra khi và chỉ khi \(x =
y\) hay P, Q là trung điểm của BC, DA
Ta có: \(\left| \overrightarrow{MP} +
\overrightarrow{MQ} + \overrightarrow{MR} \right|^{2} = (x + y + z)^{2}
+ t^{2} \geq (1 + z)^{2} + t^{2} = \left| \overrightarrow{MH}
\right|\)
Khi P ≡ P∗, R ≡ R∗, Q thay đổi trên AC, H sẽ thay đổi trên đoạn thẳng DK sao cho tam giác DCK vuông cân tại C.
Ta lại có: \(\widehat{MDH} \approx 108^{0}
\Rightarrow MH \geq MD = \frac{a\sqrt{5}}{2}\).
Bài tập 4. Cho tam giác ABC đều cạnh \(a\). Đường thẳng \(\Delta\) qua \(A\) và song song với \(BC\), lấy điểm \(M \in \Delta\). Tính giá trị nhỏ nhất của \(\left| \overrightarrow{CA} +
2\overrightarrow{MB} \right|\) khi \(M\) di động trên \(\Delta\).
Hướng dẫn giải
Hình vẽ minh họa
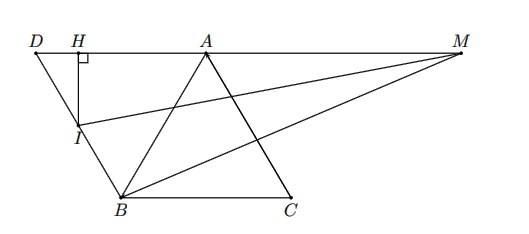
Kẻ hình bình hành ACBD. Gọi I là trung điểm BD, khi đó, ta có
Ta có:
\(\left| \overrightarrow{CA} +
2\overrightarrow{MB} \right| = \left| \overrightarrow{CA} + 2\left(
\overrightarrow{IB} - \overrightarrow{IM} \right) \right|\)
\(= \left| \overrightarrow{CA} +
2\overrightarrow{IB} - 2\overrightarrow{IM} \right| = \left|
\overrightarrow{CA} + \overrightarrow{DB} - 2\overrightarrow{IM}
\right|\)
\(= \left| \overrightarrow{CA} -
\overrightarrow{CA} - 2\overrightarrow{IM} \right|\)
\(= 2\left| \overrightarrow{IM} \right|
\geq 2IH = 2.\frac{1}{2}.\frac{a\sqrt{3}}{2} =
\frac{a\sqrt{3}}{2}\)
Dấu “=” xảy ra khi và chỉ khi M trùng với điểm H là hình chiếu vuông góc củađiểm I trên đường thẳng \(\Delta\).
Bài tập 5. Trong mặt phẳng với hệ tọa độ \(Oxy\), cho tam giác \(ABC\) cân tại \(A\) có phương trình hai cạnh là \((AB):\ \ \ \ x + 2y - 2 = 0,\ \ (AC):\ \ \ \ 2x +
y + 1 = 0\), điểm \(M(1;2)\) thuộc đoạn thẳng \(BC\). Tìm tọa độ điểm \(D\) sao cho \(\overrightarrow{DB}.\overrightarrow{DC}\) có giá trị nhỏ nhất.
Hướng dẫn giải
Phương trình các đường phân giác góc A là
\(\frac{|x + 2y - 2|}{\sqrt{5}} = \frac{|2x
+ y + 1|}{\sqrt{5}} \Leftrightarrow \left\lbrack \begin{matrix}
x - y + 3 = 0 \\
3x + 3y - 1 = 0 \\
\end{matrix} \right.\)
Do Δ\(ABC\) cân tại \(A\) nên phân giác trong (\(l_{a}\)) của góc\(A\) vuông góc với BC
Trường hợp 1: \((l_{a}):x - y + 3 =
0\), khi đó \(BC\) đi qua \(M(1;2)\)và có vtpt \(\overrightarrow{n_{1}} = (1;1)\);
⇒ Phương trình cạnh \(BC\):\(x + y - 3 = 0\)
Tọa độ \(B\) :\(\left\{ \begin{matrix}
x + 2y - 2 = 0 \\
x + y - 3 = 0 \\
\end{matrix} \right.\ \Leftrightarrow \left\{ \begin{matrix}
x = 4 \\
y = - 1 \\
\end{matrix} \right.\ \Rightarrow B(4; - 1)\)
Tọa độ \(C\) :\(\left\{ \begin{matrix}
2x + y + 1 = 0 \\
x + y - 3 = 0 \\
\end{matrix} \right.\ \Leftrightarrow \left\{ \begin{matrix}
x = - 4 \\
y = 7 \\
\end{matrix} \right.\ \Rightarrow C( - 4;7)\)
Khi đó \(\overrightarrow{MB} = (3; -
3)\) ; \(\overrightarrow{MC} = ( -
5;5)\) ngược hướng ; \(B,C\) nằm hai phía (\(l_{a}\)) (thỏa mãn)
Trường hợp 2 : \((l_{a}):3x + 3y - 1 =
0\), khi đó \(BC\) đi qua \(M(1;2)\) và có vtpt \(\overrightarrow{n_{2}} = (1; - 1)\)
\(BC\bot AD;M \in BC\)⇒ Phương trình cạnh\(BC\): \(x - y + 1 = 0\)
Tọa độ \(B\) :\(\left\{ \begin{matrix}
x + 2y - 2 = 0 \\
x - y + 1 = 0 \\
\end{matrix} \right.\ \Leftrightarrow \left\{ \begin{matrix}
x = 0 \\
y = 1 \\
\end{matrix} \right.\ \Rightarrow B(0;1)\)
Tọa độ \(C\) :\(\left\{ \begin{matrix}
2x + y + 1 = 0 \\
x - y + 1 = 0 \\
\end{matrix} \right.\ \Leftrightarrow \left\{ \begin{matrix}
x = - \frac{2}{3} \\
y = \frac{1}{3} \\
\end{matrix} \right.\ \Rightarrow C( -
\frac{2}{3};\frac{1}{3})\)
Khi đó \(\overrightarrow{MB} = ( - 1; -
1)\) ; \(\overrightarrow{MC} = \left( -
\frac{5}{3}; - \frac{5}{3} \right)\) cùng hướng (loại)
Với \(B(4; - 1)\) ; \(C( - 4;7)\).
Đặt \(D(x;y) \Rightarrow
\overrightarrow{DB} = (4 - x; - 1 - y),\overrightarrow{DC} = ( - 4 - x;7
- y)\)
\(\Rightarrow
\overrightarrow{DB}.\overrightarrow{DC} = x^{2} + y^{2} - 6y - 23 =
x^{2} + (y - 3)^{2} - 32 \geq - 32\).
Dấu \('' = ''
\Leftrightarrow \left\{ \begin{matrix}
x = 0 \\
y = 3 \\
\end{matrix} \right.\)
Vậy \(D(0;3)\) thì \(\overrightarrow{DB}.\overrightarrow{DC}\) nhỏ nhất bằng -32.
--------------------------------------------
Qua bài viết, bạn đã được trang bị phương pháp xác định tọa độ điểm D sao cho biểu thức vectơ đạt giá trị nhỏ nhất – một kỹ năng quan trọng trong giải tích hình học lớp 10. Bằng cách hiểu rõ mối quan hệ giữa các vectơ, tọa độ điểm và các công thức độ dài, bạn sẽ xử lý tốt các bài toán cực trị trong mặt phẳng tọa độ.
