Tính các góc của tam giác khi biết độ dài ba cạnh của tam giác đó
Cách tính góc tam giác khi biết ba cạnh
Trong chuyên đề Hệ thức lượng trong tam giác Toán 10, việc tính các góc của tam giác khi biết độ dài ba cạnh là dạng bài tập cơ bản nhưng rất quan trọng. Bài viết này sẽ giúp học sinh hiểu rõ cách áp dụng định lý cos để tìm các góc của tam giác, đồng thời cung cấp ví dụ minh họa chi tiết, dễ hiểu và phương pháp giải nhanh. Đây là tài liệu hữu ích giúp các em nắm vững công thức, rèn luyện kỹ năng giải bài chính xác và hiệu quả.
A. Phương pháp giải toán
Cho tam giác ABC như hình vẽ:
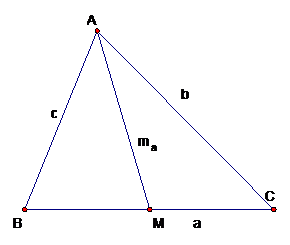
Dùng hệ quả của định côsin
\(\cos A = \frac{b^{2} + c^{2} -
a^{2}}{2bc}\) \(\cos B = \frac{c^{2} +
a^{2} - b^{2}}{2ca}\) \(\cos C =
\frac{a^{2} + b^{2} - c^{2}}{2ab}\)
Công thức tính độ dài đường trung tuyến
\(m_{a}^{2} = \frac{2\left( b^{2} + c^{2}
\right) - a^{2}}{4}\) \(m_{b}^{2} =
\frac{2\left( c^{2} + a^{2} \right) - b^{2}}{4}\) \(m_{c}^{2} = \frac{2\left( a^{2} + b^{2} \right) -
c^{2}}{4}\)
B. Ví dụ minh họa tính số đo góc của tam giác
Ví dụ 1: Cho tam giác \(ABC\) có độ dài ba cạnh là \(AB = 2\), \(BC = 3\), \(CA =
4\). Tính góc \(ABC\)?
Hướng dẫn giải
Áp dụng hệ quả của định lý côsin trong tam giác ta có:
\(\cos\widehat{ABC} = \frac{BA^{2} +
BC^{2} - AC^{2}}{2.BA.BC}\)
\(\Leftrightarrow \cos\widehat{ABC} =
\frac{2^{2} + 3^{2} - 4^{2}}{2.2.3} = \frac{- 3}{12} = \frac{-
1}{4}\).
Suy ra góc \(\widehat{ABC} \simeq
104^{0}29'\).
Ví dụ 2: Cho tam giác \(ABC\) có \(a = 2\); \(b = \sqrt{6}\); \(c = 1 + \sqrt{3}\). Tính số đo góc \(\widehat{A}\)?
Hướng dẫn giải
Ta có:
\(\cos A = \frac{b^{2} + c^{2} -
a^{2}}{2bc} = \frac{6 + \left( 1 + \sqrt{3} \right)^{2} -
4}{2.\sqrt{6}.\left( 1 + \sqrt{3} \right)} = \frac{\sqrt{2}}{2}\)
\(\Rightarrow \widehat{A} =
45^{0}\).
Ví dụ 3: Cho tam giác \(ABC\) có \(a = 2\); \(b = \sqrt{6}\); \(c = 1 + \sqrt{3}\). Góc \(\widehat{B}\) bằng bao nhiêu?
Hướng dẫn giải
Ta có
\(\cos B = \frac{a^{2} + c^{2} -
b^{2}}{2ac} = \frac{1}{2} \Rightarrow \widehat{B} = 60^{0}\).
Ví dụ 4: Tam giác \(ABC\) có các cạnh \(a\), \(b\), \(c\) thỏa mãn điều kiện \((a + b + c)(a + b - c) =
3ab\). Tính số đo của góc \(C\).
Hướng dẫn giải
Ta có: \((a + b + c)(a + b - c) =
3ab\)
\(\Leftrightarrow\) \((a + b)^{2} - c^{2} = 3ab\) \(\Leftrightarrow a^{2} + b^{2} - c^{2} =
ab\).
Mà \(\cos C = \frac{a^{2} + b^{2} -
c^{2}}{2ab} = \frac{1}{2}\) \(\Rightarrow \widehat{C} = 60^{0}\).
C. Bài tập tự rèn luyện có đáp án chi tiết
Bài tập 1: Tam giác \(ABC\) có \(AB = \frac{\sqrt{6} - \sqrt{2}}{2},\ \ BC =
\sqrt{3},\ \ CA = \sqrt{2}\). Gọi \(D\) là chân đường phân giác trong góc \(\widehat{A}\). Tìm số đo của \(\widehat{ADB}\)
Bài tập 2: Tính góc \(A\) của \(\Delta ABC,\) biết rằng \(b(b^{2} - a^{2}) = c(a^{2} - c^{2}).\)
Bài tập 3: Tam giác \(ABC\) có \(AB = 8\ cm\), \(BC = 10\ cm\), \(CA = 6\ cm\). Tìm độ dài đường trung tuyến \(AM\) của tam giác.
Bài tập 4: Tam giác \(ABC\) có \(AB = 9\)cm, \(AC
= 12\)cm và \(BC = 15\)cm. Tính độ dài đường trung tuyến \(AM\) của tam giác đã cho.
Không thể hiển thị hết nội dung tại đây — bấm Tải về để lấy toàn bộ tài liệu.
------------------------------------------------------------
Hy vọng bài viết Tính các góc của tam giác khi biết độ dài ba cạnh của tam giác đó đã giúp các em hiểu rõ cách sử dụng định lý cos trong hệ thức lượng Toán 10. Hãy luyện tập thêm nhiều bài tập hệ thức lượng trong tam giác để củng cố kiến thức và nâng cao khả năng tư duy hình học, chuẩn bị tốt cho các kỳ thi sắp tới!
