Ứng dụng biểu đồ Ven trong giải bài tập Tập hợp Toán 10
Cách giải bài tập tập hợp bằng biểu đồ Ven
Trong chuyên đề Tập hợp Toán 10, các phép toán như giao, hợp, hiệu và phần bù của hai hay nhiều tập hợp thường gây khó khăn cho học sinh nếu chỉ áp dụng công thức thuần túy. Biểu đồ Ven là một công cụ trực quan, giúp minh họa mối quan hệ giữa các tập hợp, từ đó hỗ trợ giải nhanh và chính xác các bài toán. Bài viết này sẽ giới thiệu ứng dụng biểu đồ Ven trong giải bài tập tập hợp Toán 10, đi kèm ví dụ minh họa chi tiết và phương pháp tư duy logic để học sinh dễ dàng nắm vững kiến thức.
A. Kiến thức cần nhớ
Sử dụng các biểu đồ Ven để mô tả các đại lượng và mối quan hệ giữa;
Công thức tính số phần tử
\(n(A \cup B) =
n(A) + n(B) - n(A \cap B)\)
B. Bài tập ví dụ minh họa ứng dụng biểu đồ Ven
Ví dụ 1: Lớp 10B có 28 học sinh tham gia câu lạc bộ thể thao và 19 học sinh tham gia câu lạc bộ âm nhạc. Biết rằng có 10 học sinh tham gia cả hai câu lạc bộ trên.
a) Có bao nhiêu học sinh tham gia câu lạc bộ thể thao và không tham gia câu lạc bộ âm nhạc?
b) Có bao nhiêu học sinh tham gia ít nhất một trong hai câu lạc bộ trên?
c) Biết lớp 10B có 40 học sinh. Có bao nhiêu học sinh không tham gia câu lạc bộ thể thao? Có bao nhiêu học sinh không tham gia cả hai câu lạc bộ?
Hướng dẫn giải
Gọi \(A\) là tập hợp học sinh tham gia câu lạc bộ thể thao, \(B\) là tập hợp học sinh tham gia câu lạc bộ âm nhạc, \(E\) là tập hợp học sinh cưa lớp 10 B .
Khi đó ta biểu diễn ba tập hợp trên bằng biểu đồ Ven.
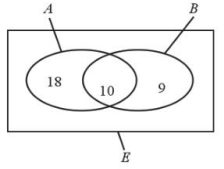
a) Tâp hợp các học sinh tham gia câu lạc bộ thể thao và không tham gia câu lạc bộ âm nhạc là tập hợp \(A\backslash B\).
Số phần tử của \(A\backslash B\) là: \(28 - 10 = 18\) (học sinh).
b) Tập hợp các học sinh tham gia it nhất một trong hai câu lạc bộ trên chính là tập hợp \(A \cup B\).
Số học sinh tham gia ít nhất một trong hai câu lạc bộ trên là: \(18 + 10 + 9 = 37\)(học sinh).
Hoặc có thể tính theo công thức: \(n(A \cup
B) = n(A) + n(B) - n(A \cap B) = 28 + 19 - 10 = 37\)(học sinh).
c) Số phần tử của \(E\)là \(40\). Tập hợp các học sinh không tham gia câu lạc bộ thể thao là phần bù của \(A\) trong \(E\).
Vậy số học sinh không tham gia câu lạc bộ thể thao là: \(40 - 28 = 12\)(học sinh).
Tập hợp các học sinh không tham gia cả hai câu lạc bộ là phần bù của \(A \cup B\) trong \(E\).
Vậy số học sinh không tham gia cả hai câu lạc bộ là: \(40 - 37 = 3\) (học sinh).
Nhận xét: Về phần trình bày các em có thể vẽ xong biểu đồ ven, dựa vào biểu đồ ven và trả lời các câu hỏi liên quan, không cần giải thích.
Ví dụ 2: Trong một cuộc phỏng vấn 56 người về những việc họ thường làm vào ngày nghỉ cuối tuẩn, có 24 người thích tập thể thao, 15 người thích đi câu cá và 20 người không thích cả hai hoạt động trên.
a) Có bao nhiêu người thích chơi thể thao hoặc thích câu cá?
b) Có bao nhiêu người thích cả câu cá và chơi thể thao?
c) Có bao nhiêu người chỉ thích câu cá, không thích chơi thể thao?
Hướng dẫn giải
Gọi A là tập hợp những người thích tập thể thao, \(B\) là tập hợp những người thích đi câu cá. \(E\) là tập hợp những người được phỏng vấn.
Khi đó ta biểu diễn ba tập hợp trên bằng biểu đồ Ven.
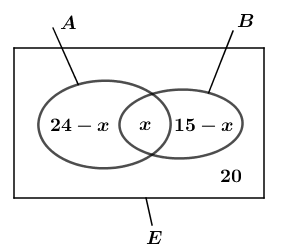
a) Số người thích chơi thể thao hoặc thích câu cá là: \(56 - 20 = 36\) (người)
b) Gọi số người thích cả câu cá và chơi thể thao là \(x,\left( x\mathbb{\in N} \right)\) .
Khi đó ta có \(24 - x + x + 15 - x = 36
\Leftrightarrow x = 39 - 36 = 3\) (người).
c) Số người chỉ thích câu cá, không thích chơi thể thao là: \(15 - 3 = 12\)(người)
C. Bài tập tự rèn luyện có hướng dẫn đáp án chi tiết
Bài tập 1: Để phục vụ cho một hội nghị quốc tế, ban tổ chức huy động 35 người phiên dịch tiếng Anh, 30 người phiên dịch tiếng Pháp, trong đó có 16 người phiên dịch được cả hai thứ tiếng Anh và Pháp. Hãy trả lời các câu hỏi sau:
a) Ban tổ chức đã huy động bao nhiêu người phiên dịch cho hội nghị đó?
b) Có bao nhiêu người chỉ phiên dịch được tiếng Anh?
c) Có bao nhiêu người chỉ phiên dịch được tiếng Pháp?
Bài tập 2: Thống kê tại một trung tâm mua sắm gồm 46 cửa hàng, với 26 cửa hàng có bán quần áo, 16 cửa hàng có bán giày và 34 cửa hàng bán ít nhất một trong hai mặt hàng này. Hỏi:
a) Có bao nhiêu cửa hàng bán cả quần áo và giày?
b) Có bao nhiêu cửa hàng chỉ bán một trong hai loại quần áo hoặc giày?
c) Có bao nhiêu cửa hàng không bán cả hai loại hàng hoá trên?
Tài liệu quá dài để hiển thị hết — hãy nhấn Tải về để xem trọn bộ!
---------------------------------------
Biểu đồ Ven không chỉ là một phương tiện minh họa trực quan, mà còn là công cụ giúp học sinh giải quyết nhanh gọn các bài toán tập hợp trong Toán 10. Việc luyện tập thường xuyên với nhiều dạng bài sẽ rèn luyện tư duy logic, khả năng phân tích và sự chính xác khi làm bài.
Ngoài ra, phương pháp này còn được ứng dụng rộng rãi trong nhiều lĩnh vực như xác suất thống kê, tin học, khoa học dữ liệu và nghiên cứu khoa học. Do đó, nắm vững cách sử dụng biểu đồ Ven từ những bài tập cơ bản trong Toán 10 sẽ giúp học sinh có nền tảng vững chắc để học tốt các chuyên đề Toán nâng cao cũng như vận dụng trong thực tiễn.
